Uji Normalitas Data


Analisis statistik sering kali memiliki asumsi-asumsi tertentu agar penarikan kesimpulan menjadi valid. Salah satu asumsi penting yang banyak dijumpai adalah asumsi normalitas. Asumsi normalitas berarti bahwa data atau hasil tertentu yang dianalisis mengikuti distribusi normal atau mendekati distribusi normal.
Distribusi normal adalah distribusi probabilitas yang simetris dan berbentuk lonceng, dengan nilai rata-rata, median, dan modus yang sama. Asumsi ini penting karena banyak metode statistik berbasis parametrik bergantung pada sifat-sifat distribusi normal untuk menghasilkan hasil yang valid. Ketika asumsi normalitas tidak terpenuhi, hasil analisis statistik bisa menjadi tidak akurat, dan seringkali metode non-parametrik atau transformasi data diperlukan untuk mendapatkan hasil yang valid.
Beberapa contoh analisis dengan asumsi normalitas yaitu:
- Regresi linear dan ANOVA terdapat asumsi dimana residual model mengikuti sebaran $\text{Normal(0}, \sigma^2\text{)}$
- Linear Discriminant Analysis (LDA) mengasumsikan variabel bebas pada setiap kelompok harus berdistribusi normal
- Pendugaan selang kepercayaan rata-rata atau proporsi mengasumsikan data mengikuti sebaran normal
Uji normalitas digunakan untuk menentukan apakah sekumpulan data mengikuti distribusi normal atau tidak. Terdapat beberapa metode untuk melakukan pengujian tersebut. Pada tulisan ini kita akan membahas 6 metode yaitu histogram dan KDE Plot, QQ Plot, Uji Komogorov-Smirnov, Uji Shapiro-Wilk, Uji Anderson-Darling dan Uji Jarque-Bera.
Histogram dan KDE Plot
Histogram adalah representasi grafis dari distribusi frekuensi data. Dalam konteks normalitas, histogram dapat digunakan untuk melihat apakah data mengikuti pola distribusi normal, yang dicirikan oleh bentuk lonceng simetris. Jika histogram menunjukkan bentuk yang mendekati distribusi normal, ini bisa menjadi indikasi awal bahwa data mungkin normal.
KDE (Kernel Density Estimate) plot adalah metode non-parametrik untuk memperkirakan distribusi probabilitas suatu variabel acak. KDE plot menyajikan garis halus yang menunjukkan distribusi data. Dalam mengecek normalitas, KDE plot berguna karena memberikan gambaran yang lebih halus dan detail dibandingkan histogram, membantu mengidentifikasi penyimpangan dari distribusi normal dengan lebih jelas.
Menggunakan histogram atau KDE Plot untuk menilai normalitas data biasanya efektif ketika jumlah data cukup banyak. Namun, jika jumlah data terbatas, histogram dan KDE Plot yang dihasilkan mungkin tidak akan memberikan gambaran yang berguna.
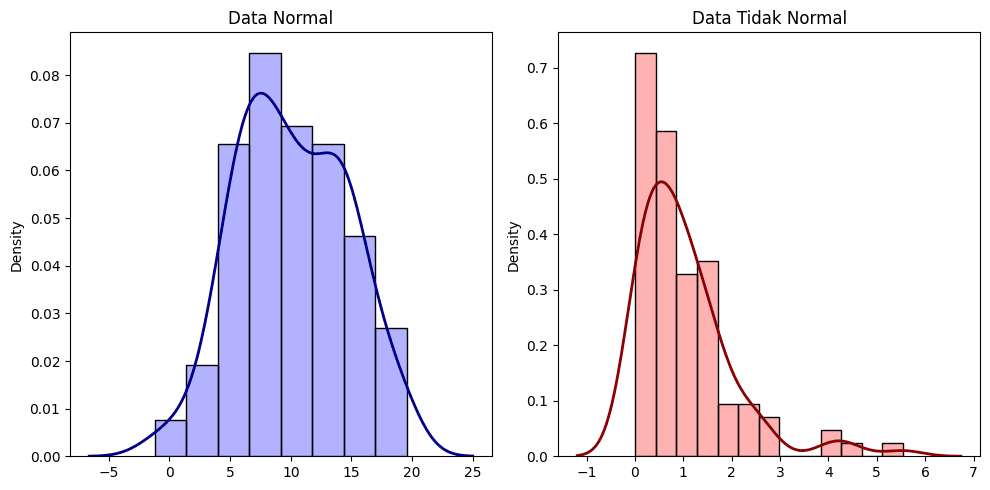
Di bawah ini ditampilkan contoh dalam bahasa R dan Python. Pada masing-masing kode, kita membangkitkan 1 set data acak berdistribusi normal dan 1 set lainnya tidak normal (misalnya dari sebaran ekponensial). Frekuensi data keduanya divisualisasikan dalam bentuk histogram dan KDE Plot untuk melihat bagaimana pola sebaran yang terbentuk. Pada data yang berdistribusi normal histogram maupun KDE plot memiliki bentuk lonceng dan cenderung simetris. Sementara pada contoh data lainnya, terdapat kecenderungan data menjulur jauh ke kanan.
Contoh:
R
set.seed(123)
# membuat 100 data acak yang berdistribusi normal(10,2)
data.normal <- rnorm(100, mean = 10, sd = 4)
# membuat 100 data acak yang tidak berdistribusi normal (exponensial)
data.not.normal <- rexp(100, rate = 1)
# Fungsi untuk plot KDE dengan histogram
plot_density <- function(data, col, main) {
hist(data, freq = FALSE,
col = adjustcolor(col, alpha.f = 0.1),
main = main, xlab = "", ylab = "Density")
lines(density(data), col = col, lwd = 2)
}
# Membuat plot dalam satu gambar
par(mfrow = c(1, 2))
plot_density(data.normal, "blue", "Data Normal")
plot_density(data.not.normal, "red", "Data Tidak Normal")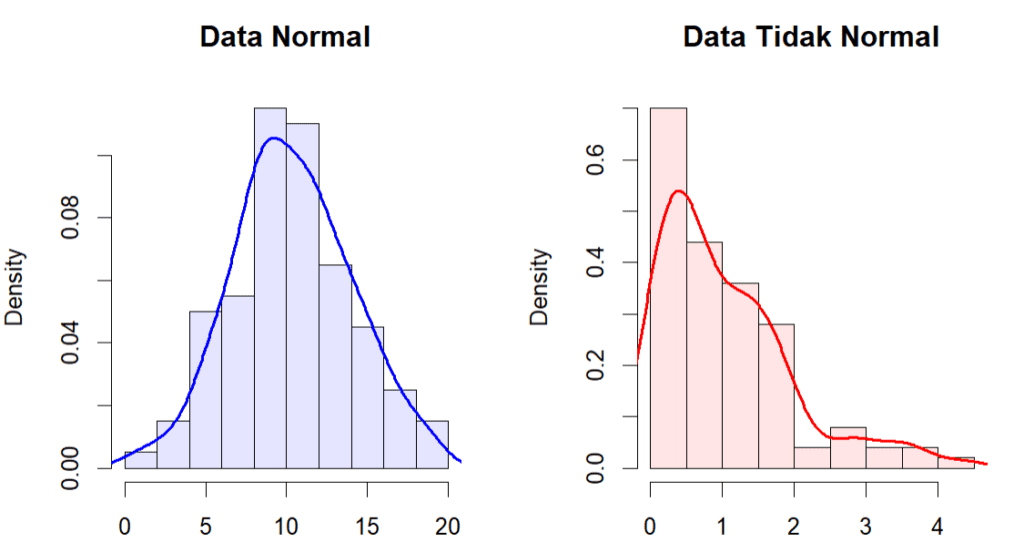

Python
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
np.random.seed(123)
data_normal = np.random.normal(loc=10, scale=4, size=100)
data_not_normal = np.random.exponential(scale=1, size=100)
# Membuat plot
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
# Plot untuk data normal
sns.histplot(data_normal, color='blue', ax=axes[0], stat='density', alpha=0.3)
sns.kdeplot(data_normal, color='darkblue', ax=axes[0], linewidth=2)
axes[0].set_title('Data Normal')
# Plot untuk data tidak normal
sns.histplot(data_not_normal, color='red', ax=axes[1], stat='density', alpha=0.3)
sns.kdeplot(data_not_normal, color='darkred', ax=axes[1], linewidth=2)
axes[1].set_title('Data Tidak Normal')
# Menampilkan plot
plt.tight_layout()
plt.show()

Quantile-Quantile Plot (QQ Plot)
QQ Plot adalah alat visual yang membandingkan kuantil data sampel dengan kuantil distribusi teoretis (dalam hal ini, distribusi normal). Pada QQ plot, data yang berdistribusi normal akan mengumpul membentuk garis lurus di sekitar garis diagonal. Jika terdapat penyimpangan yang signifikan dari garis tersebut menunjukkan bahwa data mungkin tidak mengikuti distribusi normal.
Kode berikut ini merupakan QQ Plot untuk data yang sudah dibangkitkan sebelumnya. Dapat dilihat, pada data yang menyebar normal, titik-titikd ata akan cenderung berada pada sekitar garis diagonal, sedangkan data yang tidak menyebar normal akan cenderung membentuk pola menjauh dari garis tersebut.
Contoh:
R
# Plot QQ untuk data pertama (normal)
par(mfrow=c(1,2))
qqnorm(data.normal, main="Data Normal")
qqline(data.normal, col = "red")
# Plot QQ untuk data kedua (tidak normal)
qqnorm(data.not.normal, main="Data Tidak Normal")
qqline(data.not.normal, col = "red")
title("Data Tidak Normal")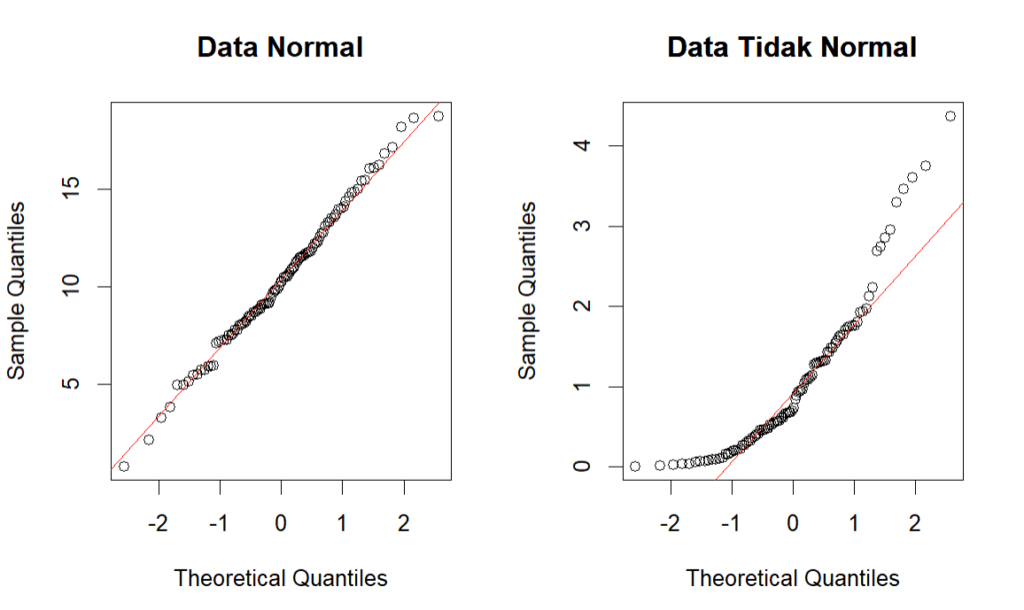

Python
import scipy.stats as stats
# Plot QQ untuk data pertama (normal)
plt.figure(figsize=(14, 6))
plt.subplot(1, 2, 1)
stats.probplot(data_normal, dist="norm", plot=plt)
plt.title('Data Normal')
plt.xlabel('Theoritical Quantiles')
plt.ylabel('Quantiles of sample data')
# Plot QQ untuk data kedua (tidak normal)
plt.subplot(1, 2, 2)
stats.probplot(data_not_normal, dist="norm", plot=plt)
plt.title('QQ Plot: Data Tidak Normal')
plt.xlabel('Theoritical Quantiles')
plt.ylabel('Quantiles of sample data')
plt.tight_layout()
plt.show()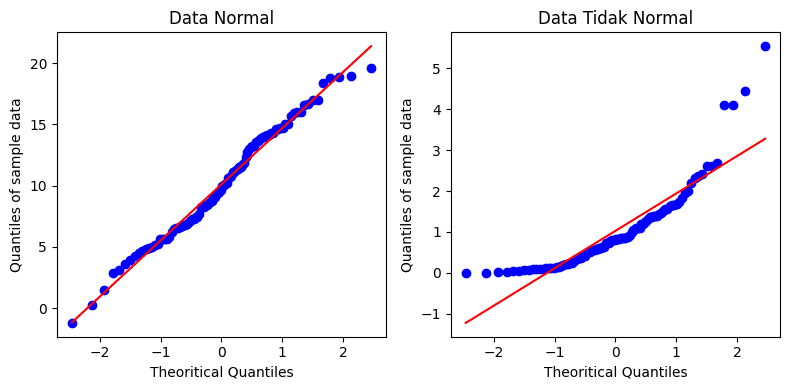

Uji Kolmogorov-Smirnov (K-S)
Uji K-S mengukur perbedaan maksimum antara fungsi distribusi kumulatif (CDF) dari distribusi data yang diamati (empiris) dan distribusi normal dengan persamaan sebagai berikut:
Formula:
$D = \max |F_n(x) – F(x)|$
Di mana:
- $D$ adalah statistik uji
- $F_n(x)$ adalah distribusi kumulatif empiris dari sampel data
- $F(x)$ adalah distribusi kumulatif teoretis (distribusi normal)
p-value yang rendah mengindikasikan data tidak mengikuti distribusi normal. Misal dengan $\alpha=\text{0.05}$, jika p-value lebih kecil dari 0.05 maka tolak $\text{H}_0$ dan disimpulkan bahwa data tidak mengikuti distribusi normal.
Contoh:
R
# Uji K-S untuk contoh data normal terhadap distribusi normal
ks_normal <- ks.test(data.normal, "pnorm",
mean = mean(data.normal),
sd = sd(data.normal))
# Uji K-S untuk data tidak normal terhadap distribusi normal
ks_not_normal <- ks.test(data.not.normal, "pnorm",
mean = mean(data.not.normal),
sd = sd(data.not.normal))
# Tampilkan hasil uji
print("Contoh Uji K-S dari data normal:")
print(ks_normal)
print("Contoh Uji K-S dari data tidak normal:")
print(ks_not_normal)# Output [1] "Uji K-S dari data normal:" Asymptotic one-sample Kolmogorov-Smirnov test data: data.normal D = 0.058097, p-value = 0.8884 alternative hypothesis: two-sided [1] "Uji K-S dari data tidak normal:" Asymptotic one-sample Kolmogorov-Smirnov test data: data.not.normal D = 0.14452, p-value = 0.03067 alternative hypothesis: two-sided
Python
from scipy.stats import kstest
# Uji K-S
ks_normal_stat, ks_normal_pvalue = kstest(
data_normal, "norm", args=(np.mean(data_normal), np.std(data_normal))
)
# Uji K-S
ks_not_normal_stat, ks_not_normal_pvalue = kstest(
data_not_normal, "norm", args=(np.mean(data_not_normal), np.std(data_not_normal))
)
# Tampilkan hasil uji
print("Hasil Uji K-S pada data normal:")
print("D:", ks_normal_stat, " P-value:", ks_normal_pvalue)
print("\nHasil Uji K-S untuk data tidak normal:")
print("D:", ks_not_normal_stat, " P-value:", ks_not_normal_pvalue)# Output Hasil Uji K-S pada data normal: D: 0.07216654946081752 P-value: 0.6480932709509453 Hasil Uji K-S untuk data tidak normal: D: 0.15155358299123356 P-value: 0.018032161471181363
Uji Shapiro-Wilk
Uji Shapiro-Wilk diukur dengan mencari suatu statistik menggunakan korelasi antara data yang diamati dan nilai harapan dari distribusi normal. Statistik yang diukur pada uji ini adalah:
Formula:
$W = \frac{\left( \sum_{i=1}^n a_i x_{(i)} \right)^2}{\sum_{i=1}^n (x_i – \bar{x})^2}$
Di mana:
- $W$ adalah statistik uji.
- $x_{(i)}$ adalah sampel data yang diurutkan.
- $a_i$ adalah koefisien yang dihitung dari rataan dan ragam.
- $\bar{x}$ adalah rata-rata sampel.
Sama seperti uji K-S, p-value yang rendah mengindikasikan data tidak mengikuti distribusi normal. Misal dengan $\alpha=\text{0.05}$, jika p-value lebih kecil dari 0.05 maka tolak $\text{H}_0$ dan dapat disimpulkan bahwa data tidak mengikuti distribusi normal.
Contoh:
R
# Uji S-W untuk data normal
sw_normal <- shapiro.test(data.normal)
# Uji S-W untuk data tidak normal
sw_not_normal <- shapiro.test(data.not.normal)
# Tampilkan hasil uji
print("Contoh Uji S-W untuk data normal:")
print(sw_normal)
print("Contoh Uji S-W untuk data tidak normal:")
print(sw_not_normal)# Output [1] "Contoh Uji Shapiro-Wilk untuk data normal:" Shapiro-Wilk normality test data: data.normal W = 0.99388, p-value = 0.9349 [1] "Contoh Uji Shapiro-Wilk untuk data tidak normal:" Shapiro-Wilk normality test data: data.not.normal W = 0.87396, p-value = 1.016e-07
Python
from scipy.stats import shapiro
# Uji S-W untuk data normal
sw_normal_stat, sw_normal_pvalue = shapiro(data_normal)
# Uji S-W untuk data tidak normal
sw_not_normal_stat, sw_not_normal_pvalue = shapiro(data_not_normal)
# Tampilkan hasil uji
print("Hasil Uji S-W pada data normal:")
print("W:", sw_normal_stat, " P-value:", sw_normal_pvalue)
print("\nHasil Uji S-W pada data tidak normal:")
print("W:", sw_not_normal_stat, " P-value:", sw_not_normal_pvalue)# Output Hasil Uji S-W pada data normal: W: 0.9841397685812812 P-value: 0.27487044002058053 Hasil Uji S-W pada data tidak normal: W: 0.8149367335344511 P-value: 7.313210786499206e-10
Uji Anderson-Darling
Uji Anderson-Darling adalah uji statistik yang lebih sensitif dibandingkan dengan uji K-S karena memberikan bobot lebih besar pada ekor-ekor distribusi.
Formula:
$A^2 = -n – \frac{1}{n} \sum_{i=1}^n (2i-1) \left[ \ln F(x_{(i)}) + \ln (1 – F(x_{(n+1-i)})) \right]$
Di mana:
- $A^2$ adalah statistik uji
- $F$ adalah distribusi kumulatif teoretis (distribusi normal)
- $x_{(i)}$ adalah sampel data yang diurutkan
Jika nilai statistik uji lebih besar dari nilai kritikal pada tingkat signifikansi tertentu, maka kita menolak hipotesis nol dan menyimpulkan bahwa data tidak mengikuti distribusi normal pada tingkat signifikansi tersebut.
Contoh:
R
library(nortest)
# Uji Anderson-Darling untuk data normal
ad_normal <- ad.test(data.normal)
# Uji Anderson-Darling untuk data tidak normal
ad_not_normal <- ad.test(data.not.normal)
# Tampilkan hasil uji
print("Uji A-D untuk data normal:")
print(ad_normal)
print("Uji A-D untuk data tidak normal:")
print(ad_not_normal)# Output [1] "Uji A-D untuk data normal:" Anderson-Darling normality test data: data.normal A = 0.182, p-value = 0.9104 [1] "Uji A-D untuk data tidak normal:" Anderson-Darling normality test data: data.not.normal A = 3.3361, p-value = 2.078e-08
Python
from scipy.stats import anderson
# Uji A-D untuk data normal
ad_normal_stat, ad_normal_crit, ad_normal_sig = anderson(data_normal, dist='norm')
# Uji A-D untuk data tidak normal
ad_not_normal_stat, ad_not_normal_crit, ad_not_normal_sig = anderson(data_not_normal, dist='norm')
# Tampilkan hasil uji
print("Hasil Uji A-D untuk data normal:")
print("A:", ad_normal_stat)
print("p-value:", ad_normal_crit)
print("Alpha:", ad_normal_sig)
print("\nHasil A-D untuk data tidak normal:")
print("Statistik:", ad_not_normal_stat)
print("Kritikal Value:", ad_not_normal_crit)
print("Alpha:", ad_not_normal_sig)# Output Hasil Uji A-D untuk data normal: A: 0.5695339672224264 Critical Value: [0.555 0.632 0.759 0.885 1.053] Alpha: [15. 10. 5. 2.5 1. ] Hasil A-D untuk data tidak normal: Statistik: 4.172108338617619 Critikal Value: [0.555 0.632 0.759 0.885 1.053] Alpha: [15. 10. 5. 2.5 1. ]
Uji Jarque-Bera
Uji Jarque-Bera menguji normalitas berdasarkan kurtosis dan skewness dari data.
Formula:
$JB = \frac{n}{6} \left( S^2 + \frac{(K-3)^2}{4} \right)$
Di mana:
- $JB$ adalah statistik uji
- $n$ adalah ukuran sampel
- $S$ adalah skewness
- $K$ adalah kurtosis
Sama seperti uji lainnya, p-value yang rendah mengindikasikan data tidak mengikuti distribusi normal. Misal dengan $\alpha=\text{0.05}$, jika p-value lebih kecil dari 0.05 maka tolak $\text{H}_0$ dan kita yakini dengan tingkat kepercayaan $1-\alpha$ bahwa data tidak mengikuti distribusi normal.
Contoh:
R
library(tseries)
# Uji J-B untuk data normal
jb_normal <- jarque.bera.test(data.normal)
# Uji J-B untuk data tidak normal
jb_not_normal <- jarque.bera.test(data.not.normal)
# Tampilkan hasil uji
print("Uji Jarque-Bera untuk data normal:")
print(jb_normal)
print("\nUji Jarque-Bera untuk data tidak normal:")
print(jb_not_normal)# Output [1] "Uji Jarque-Bera untuk data normal:" Jarque Bera Test data: data.normal X-squared = 0.16908, df = 2, p-value = 0.9189 [1] "Uji Jarque-Bera untuk data tidak normal:" Jarque Bera Test data: data.not.normal X-squared = 40.053, df = 2, p-value = 2.007e-09
Python
from scipy.stats import jarque_bera
# Uji J-B untuk data normal
jb_normal_stat, jb_normal_pvalue = jarque_bera(data_normal)
# Uji J-B untuk data tidak normal
jb_not_normal_stat, jb_not_normal_pvalue = jarque_bera(data_not_normal)
# Tampilkan hasil uji
print("Hasil Uji J-B untuk data normal:")
print("Stat.:", jb_normal_stat, " P-value:", jb_normal_pvalue)
print("\nHasil Uji J-B untuk data tidak normal:")
print("Stat.:", jb_not_normal_stat, " P-value:", jb_not_normal_pvalue)# Output Hasil Uji J-B untuk data normal: Stat.: 1.7340501908722699 P-value: 0.42019974583584685 Hasil Uji J-B untuk data tidak normal: Stat.: 171.79310051403706 P-value: 4.961376769693873e-38
Kesimpulan
Setelah penjelasan berbagai uji normalitas data statistik beserta contoh dengan visual maupun uji formal, penting untuk diingat bahwa tidak ada satu uji yang sempurna untuk semua situasi. Seringkali, kombinasi dari beberapa uji statistik dan analisis visual memberikan gambaran yang lebih lengkap tentang normalitas data. Dengan menggunakan histogram, KDE plot, Q-Q plot, serta uji-uji formal seperti Kolmogorov-Smirnov, Anderson-Darling, Shapiro-Wilk, Jarque-Bera atau uji lainnya kita dapat membuat keputusan yang lebih terkonfirmasi mengenai kesesuaian data kita dengan distribusi normal. Pendekatan ini membantu memastikan bahwa asumsi yang kita buat dalam analisis statistik lanjutan didasarkan pada evaluasi yang komprehensif dan akurat terhadap karakteristik data kita.








