Regresi Logistik untuk Klasifikasi Biner (Implementasi dengan R dan Python)

Regresi logistik adalah model klasifikasi yang digunakan untuk memprediksi respon kualitatif dengan dua kemungkinan hasil/kategori. Model regresi logistik memprediksi peluang setiap amatan untuk masuk ke salah satu dari dua kemungkinan tersebut.

Sebagai contoh, kita ingin mengelompokkan penduduk menjadi kelompok memperoleh BLT atau tidak berdasarkan (misalkan) penghasilan, jumlah anggota keluarga dan status rumah. Pada contoh ini respon terdiri dari dua kemungkinan yaitu memperoleh BLT atau tidak. Adapun peubah penjelasnya adalah penghasilan, jumlah anggota keluarga dan status rumah.

Setelah memperoleh model logistik dari data tersebut, kita dapat memprediksi misalkan diketahui penghasilan seseorang 10 juta rupiah, dengan 4 anggota keluarga dan status rumah adalah kontrak, apakah keluarga ini masuk ke dalam kelompok penerima BLT atau tidak.

Sebelum membangun model regresi logistik, kita perlu memahami tentang fungsi logistik dan perbandingan peluang (odds) sebagai dasar dari regresi logistik.

Perhatikan fungsi berikut ini:

$$p(X) = \frac{e^{\beta_0+\beta_1X}}{1+e^{\beta_0+\beta_1X}}\;\;(1)$$

Jika dilakukan transformasi maka persamaan di atas akan menjadi:

$$ln \left[ \frac{P(x)}{1-P(x)}\right] = \beta_0 + \beta_1 x \;\;(2)$$

Persamaan (1) merupakan fungsi logistik (kurvanya berbentuk sigmoid) dimana $\beta_0$ dan $\beta_1$ adalah suatu keofisien yang diketahui. Fungsi $p(X)$ untuk sembarang $X$ akan bernilai antara 0 sampai 1. Semakin kecil nominator-nya maka $p(X)$ akan menuju 0 dan sebaliknya maka $p(X)$ mendekati nilai 1. Bentuk ini cocok untuk merepresentasikan nilai peluang yang berada pada kisaran 0 sampai 1.

Selanjutnya, dari persamaan (2) merupakan bentuk regresi linear yang biasa kita kenal, hanya saja nilai respon-nya dalam bentuk logaritmik. Pada sisi kiri terdapat pembagian antara $P(x)$ dan $1-P(x)$, dimana $P(X)$ sendiri bernilai antara 0 sampai 1. Karena total nilai peluang adalah 1, maka jika kita nyatakan $P(x)$ tersebut sebagai peluang “sukses” suatu kejadian, maka $1-P(x)$ adalah peluang “gagal“-nya. Perbandingan antara peluang “sukses” suatu kejadian terhadap peluang “gagal“-nya disebut odds. Nilai odds menunjukkan seberapa besar peluang “sukses” dibandingkan peluang “gagal”. Contohnya, jika nilai odds adalah 2, artinya peluang sukses dua kali lipat dari peluang gagal dan jika nilai odds adalah 0.5, peluang sukses hanya 0,5 kali peluang gagal (peluang gagalnya 2 kali lebih besar dari peluang sukses).

Kembali ke persamaan (1) artinya kita dapat menggunakan persamaan tersebut untuk menghitung peluang sukses dari suatu kejadian. Kemudian jika kita memandang persamaan (2) sebagai suatu model regresi, maka besaran koefisien $\beta_1$ bermakna “setiap kenaikan satu satuan nilai $X$ maka akan menaikkan nilai log-odds sebanyak $\beta_1$”.

Lebih jauh, jika kita memiliki contoh acak atau data pasangan respon $Y$ yang terdiri dari dua kemungkinan nilai (“sukses” atau “gagal”) serta data $X$ sebagai penjelasnya, maka kita dapat melakukan pendugaan parameter untuk $\beta_0$ maupun $\beta_1$. Metode yang umum dalam kasus ini adalah menggunakan Maximum Likelihood (MLE) walaupun metode seperti OLS juga memungkinkan digunakan.

Perlu diingat pula, model regresi logistik akan menghasilkan nilai Peluang “sukses”. Terminologi “sukses” ini bukanlah suatu yang harus positif, namun lebih kepada apa yang menjadi perhatian peneliti. Misalkan seperti contoh di awal, kategori sukses yang dimaksud berupa masuk sebagai penerima BLT”. Dalam contoh lain peluang “sukses” bisa saja bermakna peluang seseorang akan gagal bayar jika diberikan kredit.

Secara default, threshold nilai peluang yang digunakan adalah 0.5. Jika peluang “sukses” lebih dari 0,5 yang bermakna peluang “sukses”-nya lebih besar dari peluang “gagal” maka diklasifikasikan pada kategori sukses. Sebaliknya, jika peluang “sukses”-nya lebih kecil dari peluang “gagal” maka diklasifikasikan pada kategori gagal. Namun pada kondisi tertentu nilai threshold tersebut dapat disesuaikan tergantung kebutuhan.

Sebelum mencoba dengan dataset yang lebih besar dengan variabel penjelas yang lebih banyak, sebagai contoh pertama kita akan menggunakan suatu ilustrasi yang sederhana.

Misalkan kita ingin membuat klasifikasi zona kota sebagai zona hijau atau merah, berdasarkan skor kebersihan kota tersebut. Data yang kita miliki adalah sebagai berikut :

Status Kota 0 : menunjukkan zona merah dan 1 : menunjukkan zona hijau

Dalam contoh ini kita misalkan “sukses” adalah untuk kategori zona hijau.

Berikut ini adalah kode untuk mendapatkan model regresi logistik pada bahasa R dan Python. Untuk R kita menggunakan fungsi glm dari package stats sementara untuk Python menggunakan fungsi dari library statmodels.

status <- c(0, 0, 0, 0, 1, 1, 1, 1, 1, 1)
skor <- c(5.6, 5.8, 6.7, 8.3, 7.2, 7.8, 8.1, 8.5, 8.8, 9.4)

data <- data.frame(as.factor(status), skor)

# Membuat model logistik 
# Peubah respon adalah status
# Peubah penjelas adalah skor 
# untuk logistik kita gunakan family = binomial
model <- glm(status~skor, data=data, family = "binomial")

summary(model)

# OUTPUT

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.9652  -0.3540   0.2931   0.6120   1.2524  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  -12.931      7.934  -1.630   0.1031  
skor           1.772      1.044   1.696   0.0898 .
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 13.4602  on 9  degrees of freedom
Residual deviance:  7.7871  on 8  degrees of freedom
AIC: 11.787

Number of Fisher Scoring iterations: 5

# import library
import statsmodels.api as sm
import pandas as pd
 
# loading the training dataset
status = [0, 0, 0, 0, 1, 1, 1, 1, 1, 1]

# pada statmodels jika menginginkan beta-0 (intercept) 
# kita perlu membuat list [1, 1,..., 1]
intercept = [1] * 10 
skor  = [5.6, 5.8, 6.7, 8.3, 7.2, 7.8, 8.1, 8.5, 8.8, 9.4]

penjelas  = pd.DataFrame({"intercept" : intercept, "skor" : skor})

# membuat model dengan variabel respon : status
# variabel penjelas adalah : intercept + skor
log_reg = sm.Logit(status, penjelas).fit()

print(log_reg.summary())

# OUTPUT

                           Logit Regression Results                           
==============================================================================
Dep. Variable:                      y   No. Observations:                   10
Model:                          Logit   Df Residuals:                        8
Method:                           MLE   Df Model:                            1
Date:                Sat, 26 Mar 2022   Pseudo R-squ.:                  0.4215
Time:                        20:08:20   Log-Likelihood:                -3.8936
converged:                       True   LL-Null:                       -6.7301
Covariance Type:            nonrobust   LLR p-value:                   0.01723
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
intercept    -12.9314      7.934     -1.630      0.103     -28.482       2.619
skor           1.7718      1.044      1.696      0.090      -0.275       3.819
==============================================================================

Dari output tersebut kita memperoleh nilai $\beta_0 = -12,931$ dan $\beta_1 = 1.772$, sehingga model regresi logistik untuk data di atas menjadi:

$$p(X) = \frac{e^{-12,931+1,772X}}{1+e^{-12,931+1,772X}}\;\;(3)$$

$$atau$$

$$ln \left[ \frac{P(x)}{1-P(x)}\right] = -12,931+1,772X\;\;(4)$$

Jika kita buat plot data tersebut terhadap model regresi logistiknya (dalam R) maka hasilnya sebagai berikut :

R

library(ggplot2)
ggplot(data, aes(x=skor, col=factor(status))) +
geom_point(aes(y=status), size=3) +
geom_function(fun=px, xlim = c(4, 11), color="orange", lwd=1.2) +
scale_color_manual(values = c("1" = "green",  "0" = "red"))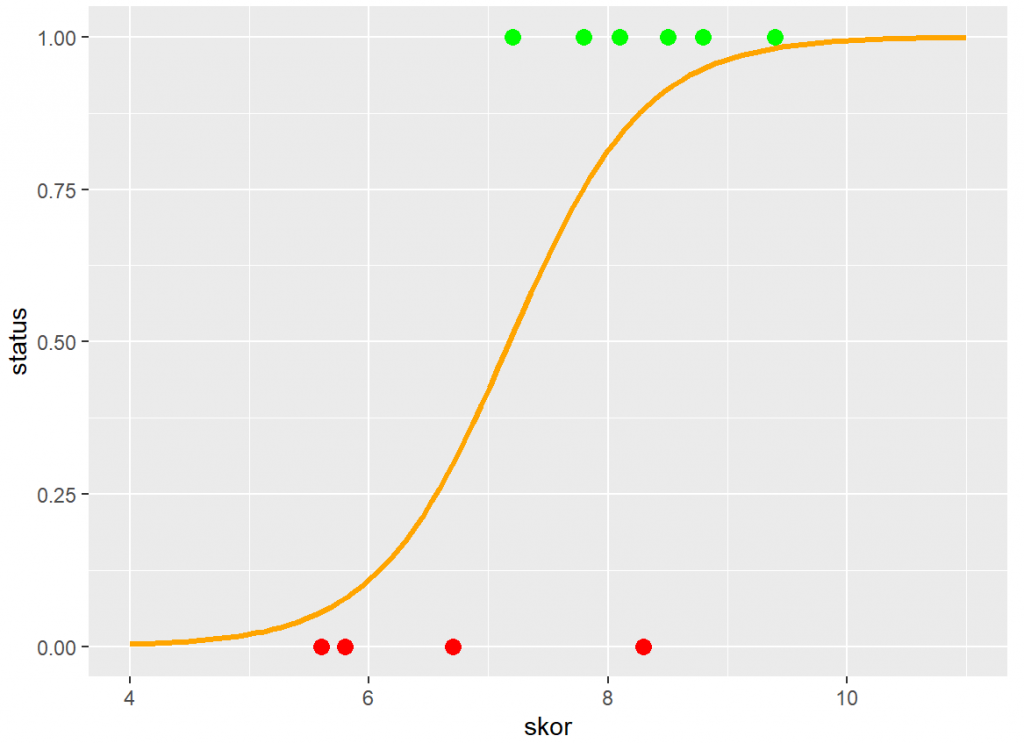

Dari model yang telah dibuat, kita dapat melakukan prediksi terhadap data baru. Misal kita memiliki informasi suatu kota memiliki skor kebersihan 8.0, berdasarkan model ini berapa peluang suksesnya (masuk zona hijau) dan pada kelompok mana kita klasifikasikan kota tersebut?

Kita dapat menentukan peluangnya melalui persamaan (3) dengan memasukkan nilai $X = 8.0$,

$$p(X=8.0) = \frac{e^{-12,931+1,772(8.0)}}{1+e^{-12,931+1,772(8.0}} = 0,776 $$

Peluang dari kota tersebut masuk zona hijau adalah sebesar 0,776, sehingga kita akan klasifikasikan kota tersebut masuk ke dalam zona hijau.

Dalam bahasa R dan python, untuk melakukan prediksi kita bisa menggunakan kode sebagai berikut:

# menghitung nilai peluang sukses 
# untuk memperoleh nilai peluang : tentukan type = "response"
# jika tidak maka outputnya adalah nilai log-odds nya.
px <- predict(model, newdata = data.frame(skor=8.0), type = "response")

zona <- ifelse(px > 0.5, 1, 0)

cat("Peluang = ", px, "zona : ", zona)

# Output
# Peluang =  0.7760577 zona :  1

# Data baru jika skor kebersihan = 8.0
newdata =  pd.DataFrame({"intercept" : [1], "skor" : [8.0]})

p = log_reg.predict(newdata)

zona = 1 if p[0] > 0.5 else 0

print(f'peluang {p[0]},  zona {zona}')

# Output
# peluang 0.776057725343657,  zona 1

Pada contoh ini, kita menggunakan ilustrasi data yang sederhana, hanya terdiri dari 10 amatan dan satu peubah penjelas. Selanjutnya kita akan mencoba dengan dataset yang lebih besar baik dari jumlah amatannya maupun jumlah peubah penjelasnya.

Untuk contoh regresi logistik berganda, kita akan menggunakan dataset social_network_ads.csv yang dapat diunduh di sini. Dataset terdiri dari 400 baris dan 5 kolom yaitu User Id, Gender, Age, EstimatedSalary, Purchased. Berdasarkan dataset ini, kita ingin membuat model untuk memprediksi apakah seseorang akan membeli suatu produk atau tidak berdasarkan informasi gender, umur dan perkiraan penghasilannya.

• Kolom User Id : akan kita abaikan karena hanya merupakan identitas data tidak ada kaitan dengan dengan kemungkinan seseorang membeli produk atau tidak
• Kolom Gender : peubah kategorik yang berisi jenis kelamin. Peubah ini akan kita pakai dalam model kita, karena tahap awal kita dapat menduga terdapat perbedaan pilihan antar gender yang berbeda terhadap keputusan membeli suatu produk atau tidak
• Kolom Age dan EstimatedSalary : kolom numerik yang berisi informasi umur dan perkiraan penghasilan, dua peubah ini juga akan kita gunakan dalam model untuk memprediksi keputusan seseorang akan membeli suatu produk atau tidak
• Kolom Purchased : peubah kategorik yang berisi (0 : tidak membeli, 1: membeli), peubah ini merupakan peubah yang akan menjadi peubah respon pada model yang dibangun.

Sebagai catatan, dataset ini sudah clean, sehingga kita tidak melakukan preprocessing data apapun.

data <- read.csv("Social_Network_Ads.csv")

# Mengubah kolom purchased menjadi faktor 1 : "membeli" 0 : "tidak membeli"
# dalam dataset kita data sudah dalam bentuk 0 dan 1
data$Purchased <- factor(data$Purchased)

# mengubah kolom gender menjadi faktor
data$Gender <- as.factor(data$Gender)

# kita bisa menghilangkan kolom ID
# karena tidak diperlukan
data["User ID"] <- NULL

# Gunakan nilai seed yang sama 
# jika ingin mendapat sampel acak sama dengan hasil di sini
set.seed(47)

# Membagi dataset menjadi 70% : train dan 30% : test
# 1. Menarik sampel acak
smp.index <- sample(x = nrow(data), size = 0.7*nrow(data))
# 2. ambil 70% tersebut sebagai data training
data.train <- data[smp.index,]
# 3. sisanya 30% sebagai data testing
data.test <- data[-smp.index,]

# Membangun model berdasarkan data training
# kolom "Purchased" sebagai peubah respon
# dan selebihnya sebagai peubah penjelas
# dapat ditulis Purchased~Gender+Age+EstimatedSalary
logit.model <- glm(Purchased~. , data = data.train, family = "binomial")

# Memprediksi data test
pred.good <- predict(logit.model, newdata = data.test, type="response")

# Menggunakan library caret
# untuk membuat confusion Matrix
#k <= 0.5 menjadi 0 dan > 0,5 menjadi 1
caret::confusionMatrix(factor(round(pred.good)), 
                       reference = data.test$Purchased)

# OUTPUT

Confusion Matrix and Statistics

          Reference
Prediction  0  1
         0 66 15
         1  5 34
                                          
               Accuracy : 0.8333          
                 95% CI : (0.7544, 0.8951)
    No Information Rate : 0.5917          
    P-Value [Acc > NIR] : 1.097e-08       
                                          
                  Kappa : 0.6438          
                                          
 Mcnemar's Test P-Value : 0.04417         
                                          
            Sensitivity : 0.9296          
            Specificity : 0.6939          
         Pos Pred Value : 0.8148          
         Neg Pred Value : 0.8718          
             Prevalence : 0.5917          
         Detection Rate : 0.5500          
   Detection Prevalence : 0.6750          
      Balanced Accuracy : 0.8117          
                                          
       'Positive' Class : 0 

# import library
import statsmodels.api as sm
import pandas as pd
from sklearn.metrics import confusion_matrix, accuracy_score
 
data = pd.read_csv("Social_Network_Ads.csv")

# Menambah kolom intercept
data['intercept'] = 1
# Untuk Gender karena hanya ada dua pilihan
# kita ubah menjadi 0 1
data['Gender'] = [1 if i =='Male' else 0 for i in data['Gender']]

# Membagi data set menjadi train dan test
# data train dipilih secara acak sebanyak 70%
data_train = data.sample(frac=0.7, random_state=47)
# data test dipilih selain data train
data_test = data.loc[~data['User ID'].isin(data_train['User ID'])]

# Membuat model berdasarkan data train
# variabel respon : Purchased
# variabel penjelas : lainnya
Xtrain = data_train[['intercept', 'Gender', 'Age', 'EstimatedSalary']]
ytrain = data_train['Purchased']
log_reg = sm.Logit(ytrain, Xtrain).fit()

# Menguji model dengan data Test
Xtest = data_test[['intercept', 'Gender', 'Age', 'EstimatedSalary']]
ytest = data_test['Purchased']
pred = [0 if p <=0.5 else 1 for p in log_reg.predict(Xtest)]

con_matrix = confusion_matrix(data_test['Purchased'], pred)
akurasi = accuracy_score(data_test['Purchased'], pred)
spesifisitas = con_matrix[0,0]/con_matrix[0].sum()
sensitifitas = con_matrix[1,1]/con_matrix[1].sum()

print(con_matrix)
print("Akurasi:",  akurasi)
print("Sensitifitas",  sensitifitas)
print("Spesifisitas",  spesifisitas)

# Output

# pada python baris menunjukkan reference
# kolom menunjukkan prediction
[[66 13]
 [ 9 32]]

Akurasi: 0.8166666666666667
Sensitifitas 0.7804878048780488
Spesifisitas 0.8354430379746836

Berdasarkan evaluasi pada data test (Untuk model Bahasa R) , model memiliki akurasi sekitar 0,83. Artinya model ini bisa kita katakan baik. Nilai sensitivity (true positive) sangat baik yaitu sekitar 0,93, atau dapat kita katakan model kita mampu memprediksi secara benar 93 persen orang yang tidak membeli produk tersebut. Namun untuk nilai specificity (true negative) nilainya tidak terlalu tinggi yaitu 0,69, atau model hanya benar 69% memprediksi orang yang ingin membeli suatu produk.

Untuk melihat koefisen setiap peubah dari model (intercept, $\beta_1, …, \beta_k$) dapat menggunakan fungsi ceof atau coeficent.

Model dari Bahasa Python memiliki akurasi sekitar 0,82. Artinya model bisa dikatakan cukup baik. Nilai sensitivity (true positive) sangat baik yaitu sekitar 66/(66+13) = 0,8354, dengan kata lain model mampu memprediksi secara benar 83,54% orang yang tidak membeli produk tersebut. Begitu pula untuk nilai specificity (true negative) nilainya juga cukup tinggi yaitu 32/(32+9) = 0,7805 atau tepat memprediksi 78,05% orang yang ingin membeli suatu produk.

Untuk melihat koefisen setiap peubah dari model (intercept, $\beta_1, …, \beta_k$) dapat menggunakan fungsi modelname.params['var'] atau modelname.params.values.

coef(logit.model)

# Output
#    (Intercept)      GenderMale             Age EstimatedSalary 
# -1.243097e+01    1.150292e-02    2.240973e-01    4.021456e-05 

coefficients(logit.model)["Age"]

# Output
#       Age 
# 0.2240973 

log_reg.params

# Output
intercept         -15.552796
Gender              0.402146
Age                 0.292354
EstimatedSalary     0.000045

log_reg.params['Gender']

# Output
0.402146

Terdapat perbedaan hasil antara model yang diperoleh pada bahasa R dan Python. Hal ini semata-mata karena penarikan sampel acak yang berbeda antara dua bahasa tersebut. Dengan sampel yang sama, keduanya akan memberikan model yang sama.

Hasil ini juga memberi gambaran bahwa dengan data yang sama mungkin saja mengasilkan model yang berbeda dikarenakan perbedaan pemilihan data training dan data testing. Oleh karena itu dalam pemodelan sering kali dilakukan proses validasi silang (cross valadation) agar memperoleh model yang optimal. Beberapa contoh validasi silang adalah K-Fold, Leave One Out Cross Validation (LOOCV) dan sebagainya. Namun hal merupakan tema lain dan tidak akan dibahas pada tulisan ini.

Setelah model regresi logistik kita peroleh model tersebut dapat kita gunakan untuk melakukan prediksi. Misalkan terdapat seorang pelanggan perempuan, berusia 28 tahun dan penghasilan 80.000, menurut model ini akan diprediksi masuk kelompok mana?

Selamat mencoba!

• James, G., Witten, D., Hastie, T., Tibshirani, R. 2014, An Introduction to Statistical Learning with Applications in R, Springer.

• Machine Learning: K-Nearest Neighbors (KNN) dengan Python Scikit-Learn
• Python: Random Forest untuk Model Klasifikasi dengan Scikit-Learn
• Python: Random Forest untuk Model Regresi dengan Scikit-Learn
• Python: Membangkitkan Data Simulasi untuk Model Regresi dengan Numpy