Principal Component Analysis (PCA) dengan R

Principal Component Analysis (PCA) atau Analisis Komponen Utama merupakan metode dalam bidang analisis data dan pembelajaran mesin. PCA berperan penting dalam mengurangi dimensi dataset yang kompleks, menyederhanakan interpretasinya, dan meningkatkan efisiensi komputasi. Pada tutorial ini, kita akan membahas konsep PCA secara lengkap mulai dari prinsip-prinsip dasar sampai implementasinya dengan bahasa R.

PCA adalah metode statistik yang bertujuan mengubah data berdimensi tinggi menjadi bentuk berdimensi lebih rendah sambil mempertahankan informasi terpenting. Pengurangan dimensi dalam konteks PCA bukan berarti memangkas jumlah fitur atau peubah. Hal ini dicapai dengan mengidentifikasi pola melalui kombinasi linear baru dari peubah asli dengan mereduksi dimensinya menjadi beberapa komponen yang paling berpengaruh yang disebut komponen utama (principal components). Komponen utama ini bersifat ortogonal, artinya antar komponen utama tidak saling berkorelasi. Hasil komponen utama tersebut digunakan untuk memproyeksikan data asli menjadi dataset yang berdimensi lebih rendah.

PCA umumnya bermanfaat ketika kita memiliki dataset dengan banyak fitur atau variabel. Setiap fitur akan meningkatkan kompleksitas data, membuat analisis, menyajikan hubungan anta peubah secara visual, atau pembangunan model menjadi menantang. Dimensi yang tinggi dataset dapat menyebabkan berbagai masalah.

Berikut beberapa hal yang terjadi ketika kita bekerja dengan data berdimensi tinggi:

• Tantangan visualisasi: Memvisualisasikan dan memahami data dalam lebih dari tiga dimensi menjadi sulit.
• Redundansi: Beberapa fitur mungkin sangat berkorelasi, sehingga mereka menyampaikan informasi yang serupa. Redundansi ini juga dapat mengganggu hasil analisis terutama pada model-model yang terpengaruh dengan masalah multikolinieritas dan tidak jarang membuat hasil menjadi tidak valid
• Overfitting: Model dapat menjadi terlalu kompleks dan terlalu mengikuti pola dalam data, mengakibatkan generalisasi yang buruk terhadap data baru dan yang belum terlihat.
• Kompleksitas komputasi: Dengan bertambahnya jumlah fitur, sumber daya komputasi dan waktu yang dibutuhkan untuk analisis dan pemodelan meningkat secara eksponensial.

Di sinilah PCA berperan untuk mengatasi tantangan tersebut dengan mengurangi dimensi data namun tetap mempertahankan fitur-fitur esensialnya.

PCA diperoleh melalui 5 tahapan berikut ini:

Standarisasi Data: Standardisasi yaitu transformasi data sehingga semua variabel memiliki nilai rata-rata=0 dan simpangan baku= 1. Tujuan standardisasi untuk memastikan semua fitur memiliki kepentingan yang sama dalam analisis tanpa terpengaruh oleh skala data.

Membuat Matriks Kovarian: Matriks kovarian adalah sebuah matriks persegi yang elemen-elemennya menggambarkan kovarian antara setiap pasangan peubah dalam dataset. Jadi, jika kita memiliki dataset dengan $k$ variabel, maka matriks kovarian akan berukuran $k \times k$.

Menghitung Nilai Eigen dan Vektor Eigen: Nilai eigen dan vektor eigen adalah konsep matematika yang terkait dengan transformasi linier dan matriks. Dalam konteks PCA, keduanya merupakan kunci dalam mengidentifikasi komponen utama.

• Nilai eigen (λ) adalah nilai skalar non-negatif yang menunjukkan banyaknya varians yang dijelaskan oleh vektor eigen yang sesuai. Dalam PCA, nilai eigen mengkuantifikasi kepentingan setiap komponen utama.
• Vektor eigen (v) adalah vektor yang terkait dengan nilai eigen. Dalam PCA, vektor eigen mewakili arah di mana data bervariasi paling banyak. Setiap vektor eigen menunjuk ke arah tertentu dalam ruang variabel dan sesuai dengan komponen utama. Vektor eigen biasanya disajikan ternormalisasi, sehingga panjangnya adalah 1.

Mengurutkan Nilai Eigen dan Vektor Eigen: Untuk mengidentifikasi komponen utama yang paling signifikan, nilai eigen diurutkan dari nilai terbesar hingga terkecil. Hasilnya, komponen utama pertama adalah vektor eigen dengan nilai eigen terbesar dan merupakan komponen yang menjelaskan varians terbanyak. Komponen berikutnya, yaitu komponen kedua yang menjelaskan varians terbanyak kedua, dan seterusnya.

Memilih Komponen Utama: Pilih subset dari vektor eigen teratas untuk membentuk matriks transformasi. Matriks ini digunakan untuk memproyeksikan data asli ke dalam ruang berdimensi lebih rendah, menghasilkan dataset yang telah direduksi.

Transformasi Data asli: Lakukan perkalian matriks antara data asli dengan matriks komponen utama yang diperoleh sebelumnya. Hasil perkalian tersebut adalah data baru berdasarkan hasil PCA, dengan jumlah dimensi baru sebanyak komponen utama yang dipilih.

Pada bagian ini, kita akan menerapkan PCA menggunakan R. Meskipun tersedia paket-paket di R, seperti FactoMineR yang menyediakan fungsi untuk melakukan PCA dengan mudah, namun memahami langkah-langkah dari PCA sangat penting. Melakukan PCA secara manual membantu kita lebih memahami konsep dan matematika di balik teknik ini, serta memberikan wawasan yang lebih dalam tentang bagaimana PCA bekerja dan bagaimana menginterpretasi hasilnya.

Data yang akan digunakan diambil dari dataset UCI-ML Repo yaitu data Nilai IPM Kab/Kota di Pulau Jawa 2018. Secara ringkas, dataset berisi informasi tentang nilai IPM dengan beberapa indikator pendidikan dan kesehatan dari 119 Kabupaten/Kota di Pulau Jawa Tahun 2018. Data terdiri dari 17 kolom, termasuk indentitas Kabupaten/Kota dan nilai IPM. Sehingga terdapat 15 variabel penjelas pada data ini yang akan kita gunakan untuk melakukan PCA.

# membaca data
data <- read.csv(
        "https://raw.githubusercontent.com/sainsdataid/dataset/main/data_ipm_jawa_2018.csv"
    )

# menampilkan struktur data
str(data)

# menjadikan kolom id sebagai identitas baris
row.names(data) <- data$id
data$id <- NULL

# slicing variabel prediktor
X <- subset(data, select=-ipm_2018)

# OUTPUT

'data.frame':	119 obs. of  17 variables:
 $ id                : int  3101 3171 3172 3173 3174 3175 3201 3202 3203 3204 ...
 $ ipm_2018          : num  70.9 84.4 82.1 81 80.9 ...
 $ PR_NO_LIS         : num  0 0 0 0 0 ...
 $ PR_SAMPAH         : num  0 0 0 0 0 ...
 $ PR_TINJA          : num  0 0.0154 0.0308 0 0 ...
 $ PR_MKM_SUNGAI     : num  0 0.615 0.446 0.25 0.304 ...
 $ PR_SUNGAI_LMBH    : num  0 0.169 0.369 0.432 0.679 ...
 $ PR_KUMUH          : num  0.167 0.369 0.554 0.841 0.679 ...
 $ PRA_1000          : num  0.787 0.199 0.228 0.255 0.134 ...
 $ SD_1000           : num  0.829 0.311 0.279 0.398 0.234 ...
 $ SM_1000           : num  0.622 0.219 0.233 0.287 0.172 ...
 $ RS_PKS_PDK_1000   : num  0.331 0.337 0.298 0.393 0.269 ...
 $ LIN_BID_POS_P_1000: num  0.29 0.1046 0.1626 0.0552 0.1242 ...
 $ APT_OBT_1000      : num  0.0414 0.1349 0.1488 0.2293 0.2583 ...
 $ DOK_DRG_1000      : num  0.373 0.212 0.448 0.313 0.262 ...
 $ BID_1000          : num  1.906 0.0868 0.2123 0.04 0.1309 ...
 $ GZ_BURUK_1000     : num  0.16574 0.00757 0.00343 0.01622 0 ...

Proses standardisasi di R dapat dilakukan menggunakan fungsi scale. Secara default, fungsi scale akan mentransformasi data sehingga memiliki nilai rata-rata 0 dan simpangan baku 1.

# standardisasi data
scaled.X <- scale(X)

# hanya untuk pengecekan saja
scaled.mean <- apply(scaled.X, 2, mean)   # mengecek nilai rata-rata setelah standardisasi
scaled.sd <- apply(scaled.X, 2, sd)       # mengecek nilai simpangan baku setelah standardisasi

check <- data.frame(
  Rataan = round(scaled.mean, 4),
  SimpanganBaku = round(scaled.sd, 4)
)

print(check)

# OUTPUT

                   Rataan SimpanganBaku
PR_NO_LIS               0             1
PR_SAMPAH               0             1
PR_TINJA                0             1
...                     .             .
DOK_DRG_1000            0             1
BID_1000                0             1
GZ_BURUK_1000           0             1

Matriks kovarian dapat dihitung menggunakan fungsi cov. Output dari fungsi cov adalah matriks persegi berukuran $k \times k$ dengan k adalah banyaknya variabel.

Jika ingin divisualisasikan, kita dapat menggunakan fungsi corrplot dari paket corrplot untuk menampilkan matriks kovarian tersebut.

R

cov.matrix <- cov(scaled.X)

# menampilkan hasil matriks kovarian
# cov.matrix

corrplot::corrplot(cov.matrix, order = "hclust", 
                   tl.col = "black", tl.srt = 4, tl.cex = 0.55)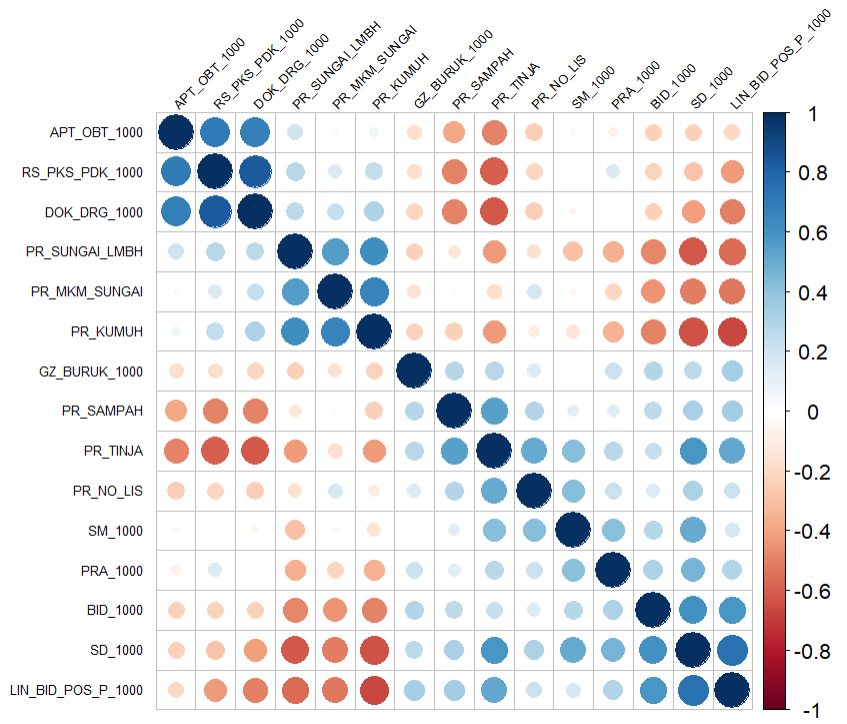

Gambar 1. Matriks Kovarian Variabel Penjelas

Nilai eigen dan vektor eigen diperoleh dari dekomposisi matriks kovarian. Dekomposisi matriks pada bahasa R dilakukan dengan fungsi eigen. Fungsi eigen menghasilkan 2 output yaitu values yang berisi nilai eigen dan vectors berisi vektor eigen. Selanjutnya, nilai eigen dan vektor eigen diurutkan dari nilai terbesar berdasarkan nilai eigen.

# Hitung nilai eigen dan vektor eigen
eigen.decomp <- eigen(cov.matrix)

# Lihat hasil
eigen.vals <- eigen.decomp$values
eigen.vecs <- eigen.decomp$vectors

# Urutkan nilai eigen dan vektor eigen
sorted.idx <- order(eigen.vals, decreasing = TRUE)
sorted.eigen.vals <- eigen.vals[sorted.idx]
sorted.eigen.vecs <- eigen.vecs[, sorted.idx]

cat("NILAI EIGEN (terurut):\n\n")
print(sorted.eigen.vals)

cat("\nVEKTOR EIGEN:\n\n")
print(sorted.eigen.vecs)

# OUTPUT

NILAI EIGEN (terurut):

 [1] 5.7567470 2.4031030 1.6861602 0.9886509 0.7064174 0.6475816 ...
[14] 0.1326907 0.1109538

VEKTOR EIGEN:

            [,1]          [,2]        [,3]  ...      [,14]       [,15]
 [1,]  0.1693726  0.1532289732 -0.50199776  ...  0.03155927 -0.05255605
 [2,]  0.2289500  0.2688610201 -0.07129785  ...  0.10894327  0.04764791
 [3,]  0.3245577  0.1973194822 -0.19812848  ... -0.34999958  0.11337546
 [4,] -0.2214572  0.3138626526 -0.38466032  ... -0.08095874  0.01069225
 [5,] -0.2908195  0.2321538395 -0.07054322  ...  0.08313638 -0.10087018
  ...        ...           ...         ...  ...         ...         ... 
[13,] -0.2858118 -0.3577473382 -0.17343194  ...  0.46625515 -0.37495180
[14,]  0.2696940 -0.2009826434  0.05790328  ... -0.33650114  0.03704500
[15,]  0.1708271  0.0009291032  0.03523564  ...  0.04845401 -0.01328979

Nilai eigen menunjukkan banyaknya keragaman data yang bisa dijelaskan oleh setiap komponen utama. Nilai ini biasa disajikan dalam bentuk persentase, sehingga lebih mudah diinterpretasikan. Selanjutnya berdasarkan kumulatif persentase varians tersebut, kita dapat memutuskan berapa banyak komponen utama yang akan digunakan untuk transformasi data asli. Hasil di bawah ini menunjukkan bahwa komponen utama pertama dapat menjelaskan sekitar 38,378 persen keragaman data. Sementara itu, akumulasi keragaman yang dapat dijelaskan oleh 5 komponen utama adalah sebesar 76,941.

# Hitung total nilai eigen
tot.eigen <- sum(eigen.vals)

var.pc <- sapply(sorted.eigen.vals, function(x) x/tot.eigen)*100

print(var.pc)

cat("\nTotal keragaman (5 PC):", sum(var.pc[1:5]))

# OUTPUT

 [1] 38.3783132 16.0206869 11.2410683  6.5910057  ...
[12]  1.5285950  1.2267825  0.8846046  0.7396917

Total keragaman (5 PC): 76.94052

Data hasil PCA diperoleh dengan melakukan perkalian antara matriks data asli dengan vektor eigen dari komponen utama yang dipilih (misal 5). Perkalian ini menghasilkan data baru dengan jumlah dimensi sebanyak 5 kolom. Jika berbicara tentang pemodelan dengan memanfaatkan PCA, maka, hasil transformasi ini selanjutnya akan menjadi dataset untuk pemodelan.

# memilih 5 komponen utama
selected.eigen.vecs <- sorted.eigen.vecs[, 1:5]

# Proyeksikan data asli ke ruang berdimensi lebih rendah
pca.result <- scaled.X %*% selected.eigen.vecs

# Ubah menjadi data frame (jika diperlukan)
pca.X <- as.data.frame(pca.result)
colnames(pca.X) <- paste("PC", 1:5, sep = "")
# pca.X$Status <- status.ipm

head(pca.X)

# OUTPUT

             PC1          PC2         PC3           PC4           PC5
3101  2.74297288 -3.346224284 -0.77193581 -0.0882139240  4.9052523150
3171 -3.43887971  2.035638791 -0.08259512 -0.5900052017  0.5702004037
3172 -3.84562076  1.625300929 -0.11576708 -0.3493788623  0.8324029674
3173 -4.31523687  1.386047681 -0.42851427 -0.5515463460  0.8232417753
3174 -4.60711595  2.310951334  0.62237166 -0.2895534761  0.1125376220
 ...         ...          ...         ...           ...           ...
3604  1.72762259  1.881797426 -0.85443500  0.3749967770  0.0808873931
3671 -1.92577215  0.643257089  1.57972617 -1.0892490796 -0.0160854038
3672 -0.93070974  0.282679167  0.31864772 -0.6397717632  0.4232347095
3673 -1.22673378  1.298832202 -0.00570107  0.3245433285  1.1080592158
3674 -3.22243099  1.183297219  0.99297990 -0.6789230425  0.2102571616

Paket FactoMineR menyediakan fungsi untuk PCA untuk melakukan PCA. Ringkasan output dari fungsi ini selanjutnya dapat dilihat menggunakan fungsi summary.PCA. Informasi yang disajikan dari ringkasan tersebut mencakup nilai eigen beserta kumulatifnya, termasuk kontribusi menurut individu dan variabel.

# Instal dan muat paket FactoMineR jika belum ada
library(FactoMineR)   # paket utama PCA

# Lakukan PCA dengan fungsi PCA dari FactoMineR
pca_result <- PCA(X, 
                  scale.unit = T, 
                  graph = F, 
                  ncp=15)     # ncp kita set agar menghasilkan output semua dimensi (default 5)

# menampilkan ringkasan hasil pca
summary.PCA(pca_result)

# menyajikan properti-properti yang dapat diakses
print(pca_result)

# OUTPUT

Call:
PCA(X = X, scale.unit = TRUE, graph = FALSE) 


Eigenvalues
                       Dim.1   Dim.2   Dim.3   Dim.4   Dim.5   ...  Dim.14   Dim.15
Variance               5.757   2.403   1.686   0.989   0.706   ...   0.133    0.111
% of var.             38.378  16.021  11.241   6.591   4.709   ...   0.885    0.740
Cumulative % of var.  38.378  54.399  65.640  72.231  76.941   ...  99.260  100.000

Individuals (the 10 first)
                       Dist    Dim.1    ctr   cos2    Dim.2    ctr   cos2    Dim.3    ctr   cos2  
3101               |  8.340 |  2.755  1.108  0.109 |  3.360  3.949  0.162 |  0.775  0.299  0.009 |
3171               |  4.932 | -3.453  1.741  0.490 | -2.044  1.461  0.172 |  0.083  0.003  0.000 |
3172               |  4.532 | -3.862  2.177  0.726 | -1.632  0.932  0.130 |  0.116  0.007  0.001 |
3173               |  5.231 | -4.333  2.741  0.686 | -1.392  0.677  0.071 |  0.430  0.092  0.007 |
3174               |  5.429 | -4.627  3.125  0.726 | -2.321  1.883  0.183 | -0.625  0.195  0.013 |
...

Variables (the 10 first)
                      Dim.1    ctr   cos2    Dim.2    ctr   cos2    Dim.3    ctr   cos2  
PR_NO_LIS          |  0.406  2.869  0.165 | -0.238  2.348  0.056 |  0.652 25.200  0.425 |
PR_SAMPAH          |  0.549  5.242  0.302 | -0.417  7.229  0.174 |  0.093  0.508  0.009 |
PR_TINJA           |  0.779 10.534  0.606 | -0.306  3.893  0.094 |  0.257  3.925  0.066 |
PR_MKM_SUNGAI      | -0.531  4.904  0.282 | -0.487  9.851  0.237 |  0.499 14.796  0.249 |
PR_SUNGAI_LMBH     | -0.698  8.458  0.487 | -0.360  5.390  0.130 |  0.092  0.498  0.008 |
...  

Output fungsi PCA terdiri dari beberapa properti penting yaitu:

• eig: matriks yang berisi semua nilai eigen, persentase variansi, dan persentase kumulatif dari variansi
• var: sebuah daftar matriks yang berisi semua hasil untuk variabel aktif (coord: koordinat , cor: korelasi antara variabel dan sumbu, cos2: cosinus kuadrat, contrib: kontribusi)
• ind: daftar matriks yang berisi semua hasil untuk individu aktif (coord: koordinat , cor: korelasi antara variabel dan sumbu, cos2: cosinus kuadrat, contrib: kontribusi)
• svd: berisi hasil dekomposisi matriks (vs, U dan V)
• call: berisi informasi pengaturan nilai parameter saat pemanggilan fungsi

# ubah ke data.frame agar lebih mudah diolah lebih lanjut

cat("\nNILAI EIGEN:\n\n")
eigen.vals.df <- data.frame(pca_result$eig)
print(eigen.vals.df$eigenvalue)

cat("\nVEKTOR EIGEN:\n\n")
eigen.vecs.df <- data.frame(pca_result$svd['V'])
print(eigen.vecs.df)

cat("\nDATA HASIL REDUKSI DIMENSI (5 PC):\n\n")
reduced.data.df <- pca_result$ind['coord']
print(reduced.data.df)

# OUTPUT
NILAI EIGEN:

 [1] 5.7567470 2.4031030 1.6861602 0.9886509 0.7064174 0.6475816 ...
[11] 0.2623381 0.2292892 0.1840174 0.1326907 0.1109538
---------------------------------------------------------------------

VEKTOR EIGEN:

            X1            X2          X3  ...         X14         X15
  1  0.1693726  0.1532289732 -0.50199776  ...  0.03155927 -0.05255605
  2  0.2289500  0.2688610201 -0.07129785  ...  0.10894327  0.04764791
  3  0.3245577  0.1973194822 -0.19812848  ... -0.34999958  0.11337546
           ...           ...         ...  ...         ...         ... 
 14  0.2696940 -0.2009826434  0.05790328  ... -0.33650114  0.03704500
 15  0.1708271  0.0009291032  0.03523564  ...  0.04845401 -0.01328979
---------------------------------------------------------------------

DATA HASIL REDUKSI DIMENSI (5 PC):

           Dim.1        Dim.2        Dim.3         Dim.4        Dim.5
3101  2.75457112  3.360373287  0.775199824 -0.0885869232 -4.925993432
3171 -3.45342050 -2.044246181  0.082944364 -0.5924999494 -0.572611410
3172 -3.86188139 -1.632173268  0.116256582 -0.3508561580 -0.835922657
....         ...          ...          ...           ...          ...
3673 -1.23192084 -1.304324118  0.005725176  0.3259156109 -1.112744476
3674 -3.23605655 -1.188300612 -0.997178566 -0.6817937659 -0.211146202

Scree Plot menampilkan variansi yang dijelaskan oleh setiap komponen utama dari PCA secara visual . Kita dapat dengan mudah menghasilkan scree plot menggunakan fungsi fviz_eig. Berikut contoh hasil menggunakan hasil sebelumnya:

R

library(factoextra)   # paket untuk visualisasi PCA

# membuat scree plot
screeplot <- fviz_eig(pca_result, 
                      addlabels = TRUE, 
                      ncp = 10, 
                      barfill = "skyblue", 
                      barcolor = "darkblue", 
                      linecolor = "red")

# Tampilkan scree plot
plot(screeplot)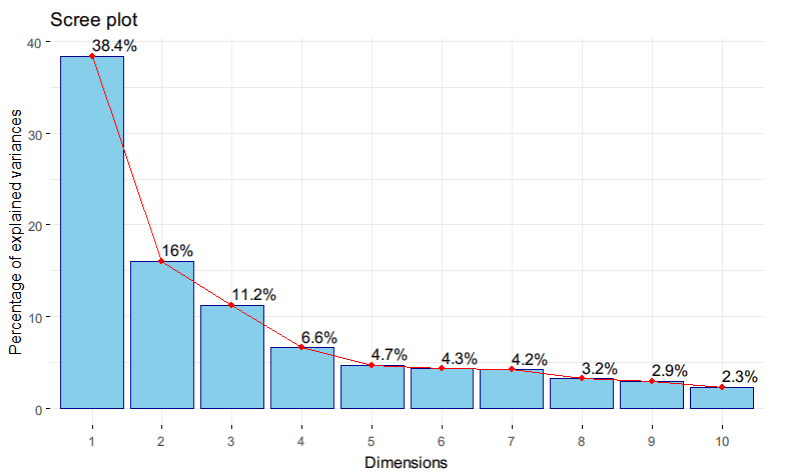

Gambar 2. Screeplot 10 Komponen Utama

Correlation circle merupakan plot yang digunakan untuk memahami hubungan antara variabel asli dalam ruang komponen utama. Pada correlation circle, setiap variabel asli direpresentasikan sebagai vektor dalam ruang komponen utama, di mana panjang vektor menunjukkan kepentingan variabel dalam komponen utama tertentu, dan sudut antara vektor-vektor mencerminkan hubungan antar-variabel. Correlation circle membantu mengidentifikasi variabel mana yang paling berkontribusi terhadap struktur data dan seberapa berkorelasi mereka dalam ruang komponen utama, memfasilitasi interpretasi dan pemahaman yang lebih baik tentang struktur data yang kompleks. Correlation circle untuk variabel dapat dibuat menggunakan fungsi fviz_pca_var dan untuk individu menggunakan fungsi fviz_pca_ind.

R

# gunakan gridExtra untuk mengelompokkan 2 atau lebih plot
library(gridExtra)

# Buat correlation circle untuk kontribusi (contrib)
contrib_circle <- fviz_pca_var(pca_result, col.var = "contrib",
                               gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), 
                               repel = TRUE) + 
                  ggtitle("Kontribusi Variabel")

# Buat correlation circle untuk cosinus kuadrat (cos2)
cos2_circle <- fviz_pca_var(pca_result, col.var = "cos2", 
                            gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), 
                            repel = TRUE) + 
               ggtitle("cos2")

# Tampilkan kedua correlation circle dalam satu grid
grid.arrange(contrib_circle, cos2_circle, ncol = 2)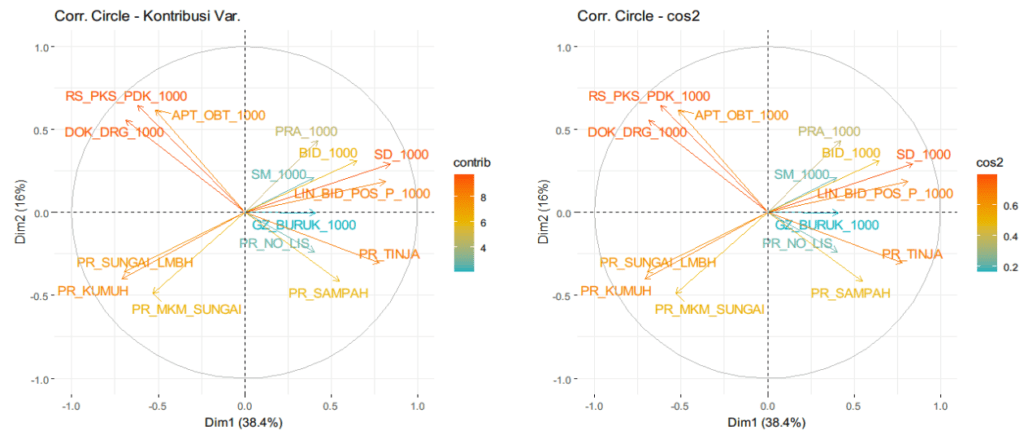

Gambar 3. Correlation Circle Kontribusi variabel dan $\text{cos}^2$

Kontribusi variabel mengukur seberapa banyak variabel atau individu berkontribusi terhadap pembentukan sumbu komponen utama tertentu. Semakin tinggi nilai kontribusi suatu variabel atau individu, semakin besar pengaruhnya terhadap pembentukan sumbu komponen utama. Kontribusi dihitung sebagai proporsi dari variasi dalam data yang dijelaskan oleh sumbu tersebut yang diberikan oleh variabel tertentu. Nilai kontribusi berkisar antara 0 hingga 100%.

Plot kontribusi dapat dibuat menggunakan fungsi fviz_contrib. Untuk menampilkan plot kontribusi variabel kita perlu mengatur parameter choice="var" dan untuk kontribusi individu choice="ind"

R

# Buat plot kontribusi variabel untuk PC1, PC2, dan PC3
contrib_v_PC1 <- fviz_contrib(pca_result, choice = "var", axes = 1, top = 5) + ggtitle("PC1")
contrib_v_PC2 <- fviz_contrib(pca_result, choice = "var", axes = 2, top = 5) + ggtitle("PC2")
contrib_v_PC3 <- fviz_contrib(pca_result, choice = "var", axes = 3, top = 5) + ggtitle("PC3")

# Tampilkan plot dalam bentuk grid
grid.arrange(contrib_v_PC1, contrib_v_PC2, contrib_v_PC3, ncol = 3)

# Buat plot kontribusi individu untuk PC1
contrib_i_PC1 <- fviz_contrib(pca_result, choice = "ind", axes = 1, top = 15) + ggtitle("PC1")

# Tampilkan plot
plot(contrib_i_PC1)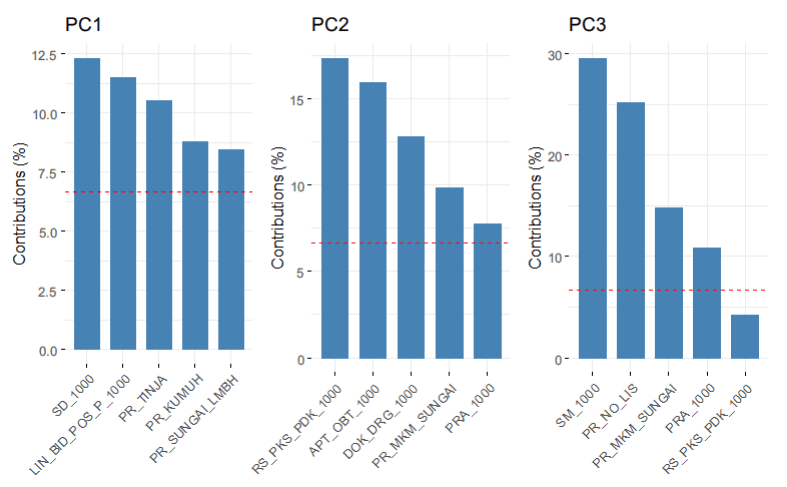

Gambar 4. Lima Variabel dengan Kontribusi Terbesar pada PC1, PC2 dan P3

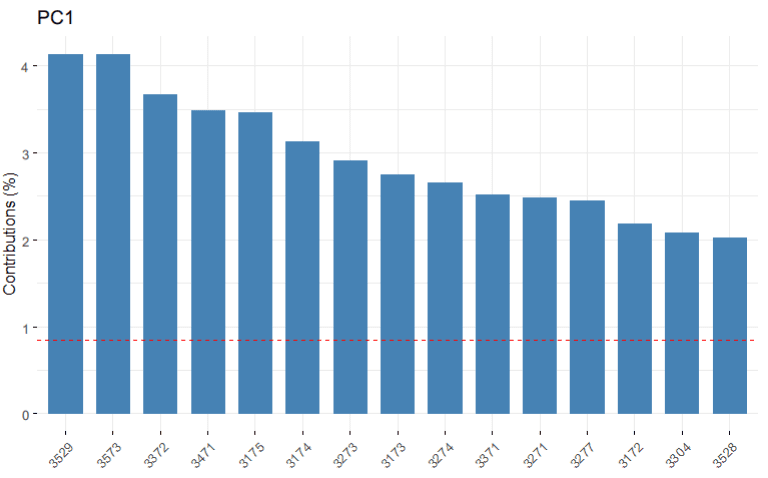
Gambar 5. Lima Belas Individu dengan Kontribusi Terbesar pada PC1

Plot cosinus kuadrat memberikan gambaran tentang seberapa baik variabel asli direpresentasikan dalam ruang komponen utama. Nilai cosinus kuadrat menunjukkan seberapa dekat posisi variabel tersebut dengan sumbu komponen utama. Semakin tinggi nilai cosinus kuadrat, semakin baik variabel tersebut direpresentasikan dalam ruang komponen utama. Plot cosinus kuadrat memungkinkan pengamatan terhadap variabel mana yang lebih relevan dan signifikan dalam menjelaskan variasi dalam data, serta membantu dalam pemilihan variabel yang paling berkontribusi dalam menerangkan struktur data.

Plot cosinus kuadrat dibuat menggunakan fungsi fviz_cos2. Sama halnya dengan plot kontribusi, pada plot cosinus kuadrat juga dapat diatur parameter choice untuk menampilkan nilai menurut variabel atau individu.

R

# Buat plot cosinus kuadrat untuk seluruh variabel
cos2_v_PC1 <- fviz_cos2(pca_result, choice = "var")

plot(cos2_v_PC1)

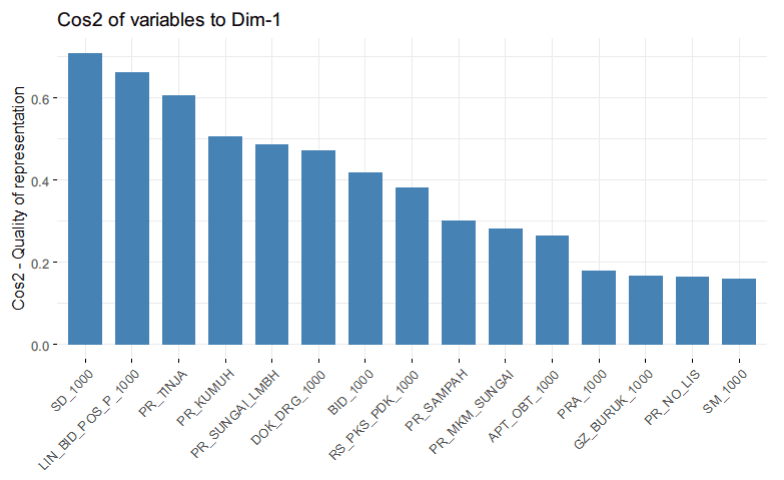
Gambar 6. Plot Cosinus Kuadrat variabel pada PC1

Biplot adalah alat visualisasi yang sering digunakan dalam analisis multivariat untuk memvisualisasikan dua jenis informasi sekaligus: (1) posisi variabel dalam ruang komponen utama (PC) dan (2) posisi individu dalam ruang komponen utama yang sama. Pada biplot, vektor-vektor variabel direpresentasikan sebagai panah dari asal koordinat ke titik di ruang PC yang mencerminkan arah dan kekuatan hubungan antara variabel tersebut. Selain itu, titik-titik yang mewakili individu juga diproyeksikan ke ruang PC, memungkinkan kita untuk melihat hubungan antara individu dan variabel dalam satu visualisasi yang kohesif.

Agar lebih informatif, pada bagian ini kita akan tambahkan peubah kategorik berdasarkan kelompok nilai IPM yaitu Rendah, Sedang, Tinggi, dan Sangat Tinggi.

R

  # kelompokkan nilai IPM
  status.ipm <- cut(data$ipm_2018,
                           breaks = c(-Inf, 60, 70, 80, Inf),
                           labels = c("Rendah", "Sedang", "Tinggi", "Sangat Tinggi"),
                           right = FALSE)

# Visualisasi Biplot
fviz_pca_biplot(pca_result, 
                geom.ind = "point", 
                col.ind = status.ipm, 
                palette = c("#FC4E07","#E7B800", "#00AFBB"), 
                addEllipses = TRUE, 
                legend.title = "Kategori")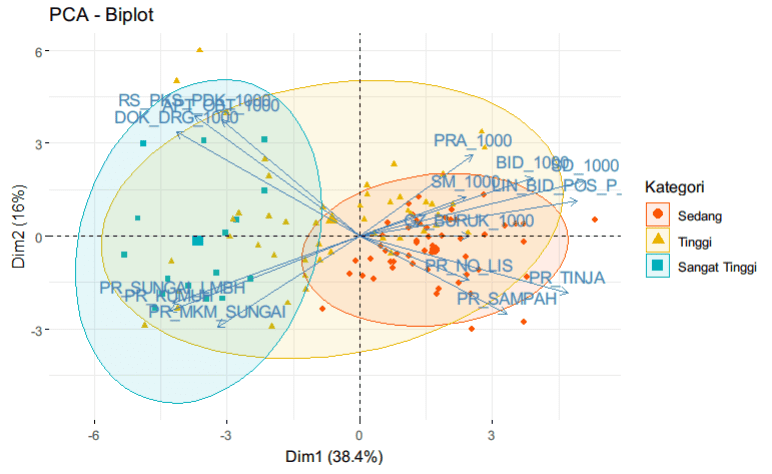

Gambar 7. Biplot Sebaran Data Menurut Kategori IPM

Pada tutorial ini, kita telah membahas analisis komponen utama (PCA) mulai dari teori hingga penerapannya dengan bahasa R. Implementasi dengan Bahasa R diawali dengan pembuatan secara manual untuk kita memahami langkah-langkah inti dalam PCA, termasuk standarisasi data, perhitungan matriks kovarian, perhitungan nilai eigen dan vektor eigen, serta seleksi komponen utama. Kemudian, kita memperdalam pemahaman PCA dengan menggunakan paket FactoMineR dan factoextra. Penggunaan paket ini dapat mempercepat proses analisis PCA dan menghasilkan visualisasi yang informatif, termasuk scree plot, biplot, correlation circle, dan lainnya. Dengan tutorial ini, diharapkan pemahaman menjadi semakin baik dan mampu menerapkannya untuk analisis data yang efektif.

• Ananda, R. 2022. Unsupervised Learning: Principal Component Analysis.
• Kurnia, A. 2024. Teknik Pembelajaran mesin [Slide Kuliah STA1382 Teknik Pembelajaran Mesin IPB University]
• Peixeiro, M. 2019. The Complete Guide to Unsupervised Learning. 
• Victor, A. 2023. An Intuitive Guide to Principal Component Analysis (PCA) in R: A Step-by-Step Tutorial with Beautiful Visualization Examples