Ukuran Penyebaran Data (Data Dispersion)


Ukuran penyebaran data adalah konsep penting dalam statistik yang menggambarkan seberapa jauh data tersebar atau bervariasi dari nilai tengahnya. Penyebaran data memberikan wawasan tentang konsistensi dan variabilitas dalam data, yang esensial untuk memahami karakteristik dasar data tersebut. Memahami ukuran penyebaran membantu peneliti dan analis data dalam membuat inferensi yang lebih akurat, mengidentifikasi outlier, dan menilai keandalan hasil analisis. Dalam berbagai bidang seperti ekonomi, sains, dan teknik, ukuran penyebaran data menjadi alat penting untuk pengambilan keputusan yang lebih tepat dan informatif.
Beberapa ukuran penyebaran yang sering digunakan dan akan dibahas pada tulisan ini adalah range, interquartile range (IQR), percentile dan standard deviation.
Range (Jangkauan)
Nilai range menunjukkan interval nilai dari keseluruhan data. Range diukur sebagai selisih nilai terbesar pada obsevasi dikurangi dengan nilai terkecilnya.
Range
Jika terdapat n data yang sudah terurut : $X_{(1)}, X_{(2)}, X_{(3)}, …, X_{(n-1)}, X_{(n)}$, maka:
$$range = X_{(n)}-X_{(1)}$$
Meskipun nilai range relatif sederhana, namun tetap memberikan informasi yang berharga mengenai keadaan data. Misalkan antara dua kelompok data yang berbeda dapat saja memiliki nilai tengah yang sama, namun dengan jangkauan yang berbeda.
Sebagai contoh pada kelas A dan kelas B memiliki nilai rata-rata ujian Matematika yang sama yaitu 75. Nilai terkecil pada kelas A adalah 30 dan nilai terbesar adalah 95. Sementara itu nilai terendah pada kelas B adalah 50 dan nilai tertinggi 90.
Pada contoh ini, range nilai dari kelas A adalah $95-30=65$ dan range kelas B adalah $90-50=40$. Hasil ini memberikan informasi yang lebih lengkap, walaupun rata-rata nilai kedua kelas sama, namun rentang nilai pada kelas A jauh lebih lebar dibandingkan nilai pada kelas B. Atau dengan kata lain, data pada kelas B cenderung lebih homogen dibandingkan kelas A.
Interquartile Range (Jangkauan antar kuartil)
Interquartile Range (IQR) menunjukkan selang nilai antara quartil ke-3 dan kuartil ke-1. Kuartil ke-1 (persentil-25) merupakan titik yang membagi data, sehingga 25% data memiliki nilai kurang dari kuartil ke-1 dan 75% lainnya memiliki nilai lebih dari kuartil ke-1. Kuartil ke-3 (persentil-75) merupakan titik yang membagi data sehingga 75% data memiliki nilai kurang dari kuartil ke-3 dan 25% lainnya memiliki nilai lebih besar dari kuartil ke-3.
Nilai IQR dapat dimaknai bahwa 50 persen data berada pada selang nilai antara kuartil ke-1 dan kuartil ke-3. Visualisasi kuartil sering dibuat dalam bentuk boxplot.
Pada data yang menyebar normal dan tanpa outlier, bentuk boxplot kurang lebih akan simetris seperti gambar berikut:
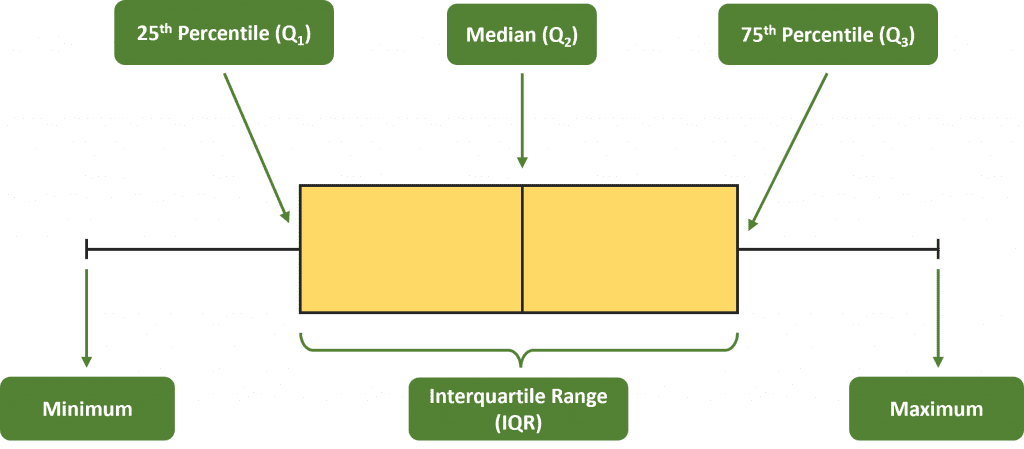

Interquartile Range
Jika terdapat n data yang sudah terurut : $X_{(1)}, X_{(2)}, X_{(3)}, …, X_{(n-1)}, X_{(n)}$, maka:
$$Q_1 = \frac{1}{4}(n+1)^{th}\,term$$
$$Q_3 = \frac{3}{4}(n+1)^{th}\,term$$
$$IQR = Q_3-Q_1$$
Contoh Soal
Misal terdapat data sebagai berikut : $2, 3, 4, 5, 5, 6, 7, 7, 9$, maka:
$$\begin{aligned}Q_1 &= \frac{1}{4}(9+1)^{th}\,term = X_{(2.5)} \\\\&= \frac{1}{2}(X_{(2)}+X_{(3)}) \\\\&=\frac{1}{2}(3+4) \\\\&=3.5 \\\\Q_3 &= \frac{3}{4}(9+1)^{th}\,term = X_{(7.5)} \\\\&= \frac{1}{2}(X_{(7)}+X_{(8)}) \\\\&=\frac{1}{2}(7+7) \\\\&=7 \\\\IQR &= 7-3.5=3.5\end{aligned}$$
Hasil perhitungan menunjukkan sekitar 50 persen data berada pada rentang nilai 3,5 hingga 7 dengan jangkauan sebesar 3,5.
Percentile (Persentil)
Nilai persentil mirip dengan kuartil. Sama halnya dengan kuartil, persentil menunjukkan posisi data sehingga bukan ukuran penyebaran data, melainkan posisi data. Untuk melihat penyebaran data menggunakan persentil, kita dapat mengambil selang persentil tertentu, misalkan selang antara persentil ke-5 dan ke-95. Nilai tersebut akan menunjukkan seperti apa penyebaran dari 90% data.
Seperti yang sudah disebutkan sebelumnya, nilai kuartil sendiri pada prinsipnya adalah nilai persentil ke-25 (kuartil ke-1), ke-50 (kuartil ke-2 atau median) dan ke-75 (kuartil ke-3). Persentil ke-p menunjukkan titik yang membagi data sehingga p% data memiliki nilai kurang dari persentil ke-p dan (100-p)% data memiliki nilai lebih besar dari persentil ke-p.
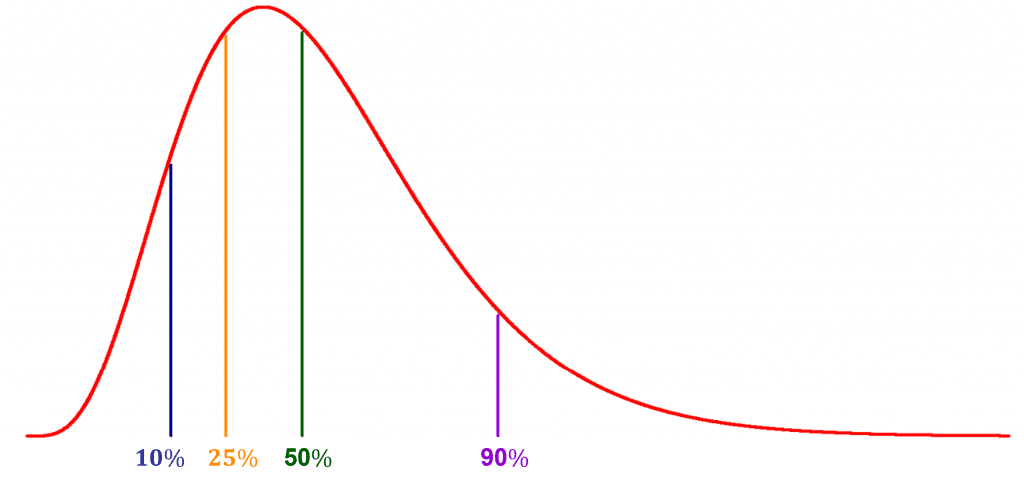

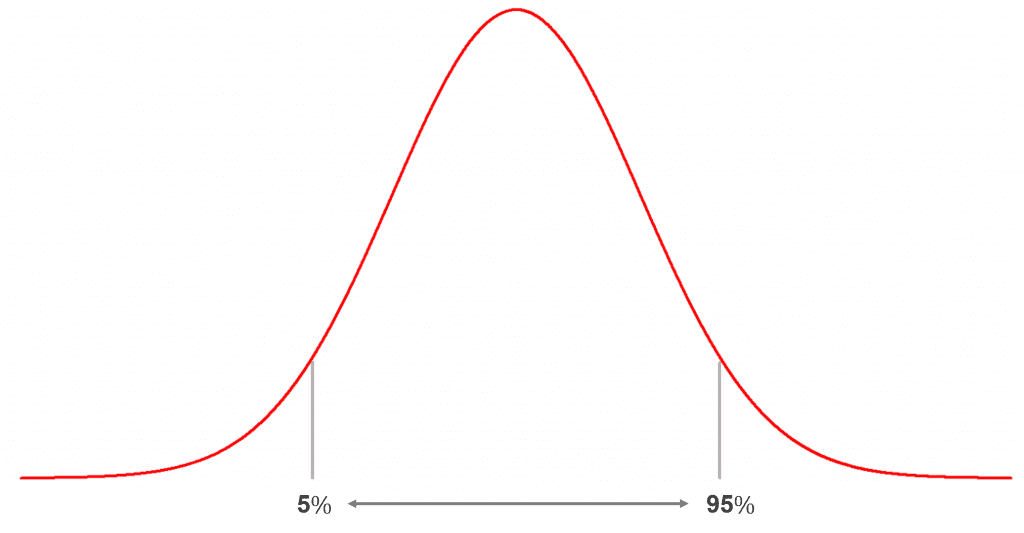

Pada ilustrasi pertama ditampilkan posisi nilai persentil ke-10, ke-25, ke-50 dan ke-90. Pada persentil ke-10, menunjukkan bahwa 10 persen data memiliki nilai kurang dari nilai persentil ke-10 tersebut. Begitu pula pada persentil ke-90 dimana 90% data memiliki nilai kurang dari persentil ke-90.
Sementara pada ilustrasi kedua, dapat dilihat bahwa sebanyak 90% data berada pada interval antara persentil ke-5 dan persentil ke-95.
Standard Deviation (Simpangan Baku)
Standar deviasi merupakan ukuran penyebaran yang paling banyak digunakan dalam bidang statistika misalnya pada pendugaan parameter dan pengujian hipotesis.
Setiap amatan memiliki simpangan terhadap nilai rataannya. Nilai simpangan ($x-\bar{x}$) akan positif jika amatan lebih besar dari nilai rataan dan sebaliknya, simpangan bernilai negatif jika amatan lebih kecil dari rataannya.
Jumlah nilai simpangan untuk seluruh amatan akan saling menghilangkan sehingga selalu bernilai 0. Oleh karena itu, untuk mengukur keragaman data dengan nilai simpangan, dapat menggunakan nilai kuadrat simpangan $(x-\bar{x})^2$ ataupun nilai absolutnya $|x-\bar{x}|$.
Adapun standar deviasi adalah akar kuadrat dari rata-rata jumlah kuadrat simpangan untuk setiap amatan (akar kuadrat dari varians). Pada data populasi, pembagi untuk kuadrat simpangan adalah $n$, sedangkan pada data sampel pembaginya adalah $n-1$.
Standar Deviasi (s)
Standar deviasi (s) dari n observasi adalah:
$$s = \sqrt{\frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}}$$
$s$ merupakan akar kuadrat dari varians ($s^2$) dimana:
$$s^2 = \frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}$$
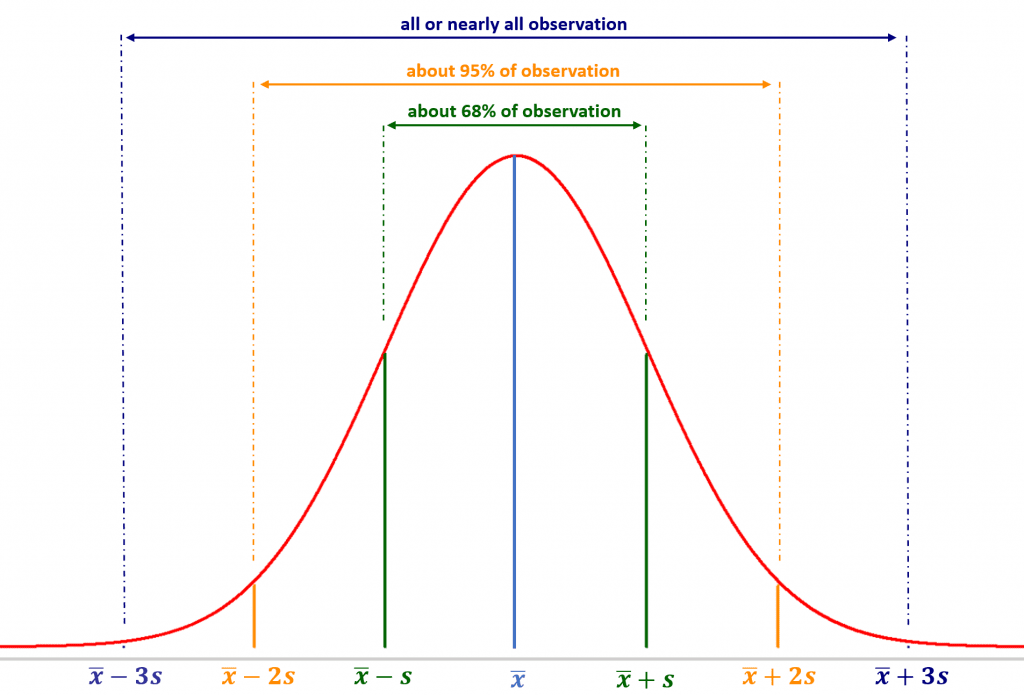
Untuk data unimodal yang menyebar simetris, bukti empiris yang menunjukkan banyaknya data yang menyebar pada selang standar deviasi tertentu, yaitu:
- Sekitar 68% dari data akan berada pada interval 1 standar deviasi dari mean yaitu $\bar{x}-s$ sampai dengan $\bar{x}+s$ atau ($\bar{x}\pm s$),
- sekitar 95% dari data akan berada pada interval 2 standar deviasi dari mean yaitu $\bar{x}-2s$ sampai dengan $\bar{x}+2s$ atau ($\bar{x}\pm 2s$),
- hampir keseluruhan data akan berada pada interval 3 standar deviasi dari mean yaitu $\bar{x}-3s$ sampai dengan $\bar{x}+3s$ atau ($\bar{x}\pm 3s$).
Gambar berikut menunjukkan bagaimana keragaman data berdasarkan standar deviasi pada sebaran simetris:

Contoh Soal
Misal terdapat data sebagai berikut : $2, 3, 4, 5, 5, 6, 7, 7, 9$, maka:
$$\begin{aligned}\bar{x} &= \frac{1}{9}(2+3+4+…+7+9) \\\\&=5.3333 \\\\s^2 &= \frac{(2-5.333)^2+(3-5.333)^2+…+(9-5.3333)^2}{9-1} \\\\&=4.75 \\\\s&= \sqrt{4.75}=2.1795\end{aligned}$$
Standar deviasi dari data tersebut adalah 2,1795.
Contoh Perhitungan dengan R
Misalkan kita memiliki 1000 data yang menyebar Normal($\mu=100$, $\sigma=10$). Kita akan menghitung berbagai ukuran yang sudah dibahas pada bagian-bagian sebelumnya menggunakan Bahasa R.
R
set.seed(100)
# Membangkitkan 1000 bilangan acak menyebar Normal(100, 10)
data <- rnorm(n=1000, mean=100, sd=10)
data <- round(data, 1)
# Nilai min dan max
nilai.min <- min(data)
nilai.max <- max(data)
# Range
range <- nilai.max - nilai.min
# Q1, Median (Q2), Q3
q1 <- quantile(data, probs=0.25, names=F)
q2 <- quantile(data, probs=0.5, names=F)
q3 <- quantile(data, probs=0.75, names=F)
# IQR
IQR <- q3 - q1
# Persentil ke-5 dan ke-95
p5 <- quantile(data, probs=0.05, names=F)
p95 <- quantile(data, probs=0.95, names=F)
# menghitung nilai rata-rata dan standar deviasi
nilai.mean <- mean(data)
nilai.sd <- sd(data)
# menghitung persentase data pada selang 1,2, 3 standar deviasi
data_1sd = length(data[(data > nilai.mean - nilai.sd) &
(data < nilai.mean + nilai.sd) ])/1000
data_2sd = length(data[(data > nilai.mean - 2*nilai.sd) &
(data < nilai.mean + 2*nilai.sd) ])/1000
data_3sd = length(data[(data > nilai.mean - 3*nilai.sd) &
(data < nilai.mean + 3*nilai.sd) ])/1000
# menampilkan histogram
hist(data, breaks=20, col="darkorange", border = 0.1)
# cetak hasil perhitungan
paste("Nilai Minimum:", nilai.min)
paste("Nilai Maksimum:", nilai.max)
paste("Nilai Range:", range)
paste("Nilai Kuartil 1:", q1)
paste("Nilai Median:", q2)
paste("Nilai Kuartil 3:", q3)
paste("Nilai IQR:", IQR)
paste("Nilai Persentil-5:", p5)
paste("Nilai Persentil-95:", p95)
paste("Nilai rata-rata:", nilai.mean)
paste("Nilai Standar Deviasi:", std)
paste("Jumlah Data pada selang rata-rata +/- 1*sd:", data_1sd)
paste("Jumlah Data pada selang rata-rata +/- 2*sd:", data_2sd)
paste("Jumlah Data pada selang rata-rata +/- 3*sd:", data_3sd)Output
Output [1] "Nilai Minimum: 66.8" [1] "Nilai Maksimum: 133" [1] "Nilai Range: 66.2" [1] "Nilai Kuartil 1: 93.5" [1] "Nilai Median: 100.4" [1] "Nilai Kuartil 3: 107.1" [1] "Nilai IQR: 13.6" [1] "Nilai Persentil-5: 82.6" [1] "Nilai Persentil-95: 116.9" [1] "Nilai rata-rata: 100.1676" [1] "Nilai Standar Deviasi: 10" [1] "Jumlah Data pada selang rata-rata +/- 1*sd: 0.687" [1] "Jumlah Data pada selang rata-rata +/- 2*sd: 0.950" [1] "Jumlah Data pada selang rata-rata +/- 3*sd: 0.998"
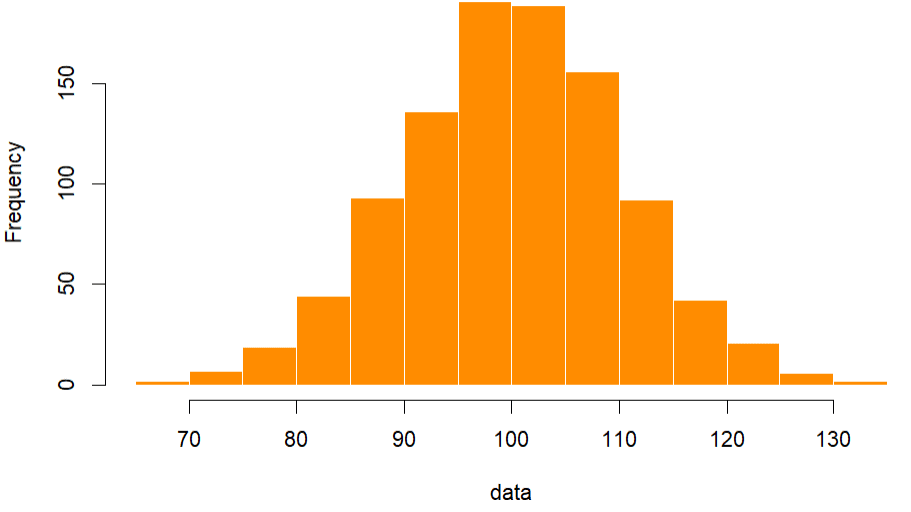

Berdasarkan hasil perhitungan pada data yang kita miliki, diperoleh nilai minimum 66,8 dan maksimum sebesar 133. Sehingga diperoleh range sebesar 66,2. Nilai kuartil 1 sebesar 93,5 menunjukkan bahwa 25% data memiliki nilai kurang dari 93,5 dan 75% data memiliki nilai lebih dari 93,5. Begitu pula untuk nilai lainnya dapat dilihat pada output di atas.
Tiga output terakhir kita mencoba melihat seberapa banyak data yang menyebar pada selang ($\bar{x} \pm 1s$), ($\bar{x} \pm 2s$), dan ($\bar{x} \pm 3s$). Hasil yang diperoleh adalah 68,7% data berada pada selang ($\bar{x} \pm 1s$), 95,0% data berada pada selang ($\bar{x} \pm 2s$) dan 99,8% data berada pada selang ($\bar{x} \pm 3s$). Hasil ini mendekati dengan apa yang sudah disampaikan sebelumnya.
Contoh Perhitungan dengan Python
Berikut ini pekerjaan yang sama dengan sebelumnya namun dibuat menggunakan bahasa python. Bilangan acak yang dibangkitkan akan berbeda dengan contoh sebelumnya karena perbedaan implementasi algoritma pada kedua bahasa.
Meskipun contoh bilangan acak yang dibangkitkan berbeda, namun ringkasan statistik yang dihasilkan seharusnya tidak akan jauh berbeda karena merupakan contoh data acak dari sebaran yang sama.
Python
import numpy as np
# membuat objek randomGenerator
rng = np.random.default_rng(seed=100)
# membangkitkan 1000 bilangan acak
data = rng.normal(loc=100, scale=10, size=1000)
data = np.round(data, 1)
# menghitungmin, max dan range
min = data.min()
max = data.max()
range = max - min
# menghitung quartil dan IQR
q1 = np.percentile(data, 25)
q2 = np.percentile(data, 50)
q3 = np.percentile(data, 75)
IQR = q3 - q1
# menghitung persentil 10 dan 90
p10 = np.percentile(data, 10)
p90 = np.percentile(data, 90)
# menghitung rata-rata dan standar deviasi
mean = data.mean()
std = data.std()
# menghitung persentase data pada selang 1,2, 3 standar deviasi
data_1sd = len(data[(data > mean - 1*std) & (data < mean + 1*std)])/1000
data_2sd = len(data[(data > mean - 2*std) & (data < mean + 2*std)])/1000
data_3sd = len(data[(data > mean - 3*std) & (data < mean + 3*std)])/1000
# mencetak hasil
print("Nilai Minimum:", min)
print("Nilai Maksimum:", max)
print("Nilai Range:", range)
print("Nilai Kuartil 1:", q1)
print("Nilai Median:", q2)
print("Nilai Kuartil 3:", q3)
print("Nilai IQR:", IQR)
print("Nilai Persentil-10:", p10)
print("Nilai Persentil-90:", p90)
print("Nilai rata-rata:", mean)
print("Nilai Standar Deviasi:", std)
print("Jumlah Data pada selang rata-rata +/- 1*sd:", data_1sd)
print("Jumlah Data pada selang rata-rata +/- 2*sd:", data_2sd)
print("Jumlah Data pada selang rata-rata +/- 3*sd:", data_3sd)Output
Output Nilai Minimum: 71.3 Nilai Maksimum: 134.3 Nilai Range: 63.000000000000014 Nilai Kuartil 1: 93.4 Nilai Median: 100.5 Nilai Kuartil 3: 107.4 Nilai IQR: 14.0 Nilai Persentil-10: 87.6 Nilai Persentil-90: 113.3 Nilai rata-rata: 100.44140000000002 Nilai Standar Deviasi: 10.088768311345047 Jumlah Data pada selang rata-rata +/- 1*sd: 0.666 Jumlah Data pada selang rata-rata +/- 2*sd: 0.957 Jumlah Data pada selang rata-rata +/- 3*sd: 0.998
Referensi
Agresti, A., Franklin, C., Klingenberg, B. (2017), Statistics The Art and Science of Learning from Data 4th Editon, Pearson Education.








