Ukuran Pemusatan Data (Central Tendency)


Ukuran pemusatan data adalah ringkasan statistik yang menunjukkan konsentrasi atau kecenderungan dimana nilai memusat pada lokasi tertentu dari sekumpulan observasi. Terdapat 3 ukuran pemusatan yang sering digunakan yaitu mean (rata-rata), median dan mode (modus).
Mean (Rata-rata)
Rata-rata adalah jumlah seluruh nilai observasi dibagi dengan banyaknya observasi. Nilai ini direpresentasikan sebagai nilai tengah atau titik keseimbangan dari sebaran data. Pada data sampel notasi yang biasa digunakan adalah $\bar{X}$ dan pada data populasi menggunakan notasi $\mu$.
Formula untuk menghitung nilai rata-rata adalah:
Rata-rata
$$\bar{X}=\frac{1}{n}\sum_{i=1}^n X_i$$
dimana $X_i$ adalah nilai dari observasi ke-i dan $n$ banyaknya observasi.
Contoh menghitung rata-rata:
- Misalkan terdapat 20 nilai hasil penelitian A sebagai berikut:
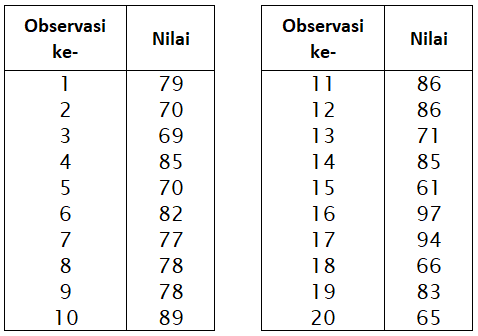

Penyelesaian
Nilai rata-rata adalah:
$$\begin{aligned}\bar{X}&=\frac{1}{20}(79 + 70 + 69 + … + 83 + 65) \\\\&=78,55\end{aligned}$$
- Tentukanlah nilai rata-rata untuk kumpulan data berikut (8, 7, 9, 9, 6, 11, 8, 10, 40, 6) !
Penyelesaian
Nilai rata-rata adalah:
$$\begin{aligned}\bar{X}&=\frac{1}{10}(8 + 7 + 9 + … + 40 + 6) \\\\&=11,4\end{aligned}$$
Terdapat data ekstrim pada contoh soal ini, hampir seluruh data memiliki nilai kurang dari 11, namun terdapat 1 nilai sangat tinggi yaitu 40. Rata-rata yang diperoleh sebesar 11,4 seolah-olah menunjukkan nilai data berada pada kisaran nilai 11, padahal sesungguhnya nilai ini adalah dampak dari outlier yang menarik nilai rata-rata menjadi jauh lebih tinggi dari mayoritas nilai seharusnya.
Median
Nilai median adalah nilai yang berada di tengah-tengah seluruh data observasi yang sudah diurutkan (dari nilai terkecil sampai nilai terbesar atau sebaliknya). Nilai median membagi data menjadi dua bagian, dimana setengah dari observasi memiliki nilai di bawah dari median, dan setengahnya lagi di atas nilai median.
Median juga dikenal robust terhadap data yang memiliki nilai outlier. Pada nilai rata-rata, keberadaan outlier akan sangat mempengaruhi hasil perhitungan dan menarik nilai rata-rata membesar atau mengecil ke arah outlier. Sedangkan nilai median, tidak akan terpengaruh oleh adanya outlier tersebut. Oleh karena itu, median juga sering dianggap ukuran pemusatan yang lebih tepat digunakan untuk kondisi sebaran data yang menjulur.
Formula untuk menghitung nilai median adalah:
Median
Misalkan terdapat n data yang sudah diurutkan sebagai berikut:
$X_{(1)}, X_{(2)}, X_{(3)}, …, X_{(n-1)}, X_{(n)}$
Jika n ganjil, maka:
$$med = X_{(\frac{n+1}{2})}$$
Jika n genap, maka:
$$med = \frac{1}{2}(X_{(\frac{n}{2})}+X_{(\frac{n}{2}+1)})$$
Contoh menghitung median:
- Menggunakan 20 data hasil penelitian A sebelumnya, hitunglah nilai median data tersebut!
Penyelesaian
Urutkan data pada observasi A:
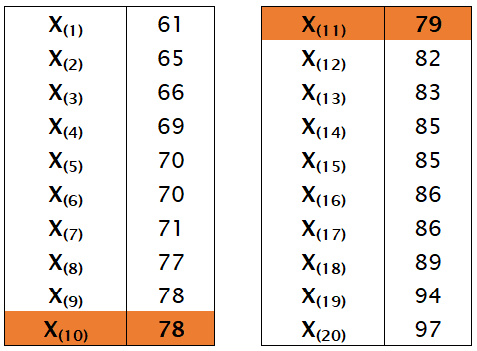

Karena n=20 genap, maka:
$$\begin{aligned}med &= \frac{1}{2}(X_{(\frac{20}{2})}+X_{(\frac{20}{2}+1)}) \\\\&=\frac{1}{2}(X_{(10)}+X_{(11)}) \\\\&=\frac{1}{2}(78+79) \\\\&=78,5\end{aligned}$$
- Tentukanlah nilai median dari data berikut (40, 45, 46, 52, 57, 64, 72, 77, 79, 80, 86) !
Penyelesaian
Karena n=11 gajil, maka:
$$\begin{aligned}med &= X_{(\frac{11+1}{2})} \\\\&=X_{(6)} \\\\&=64\end{aligned}$$
- Tentukanlah nilai median dari data berikut (8, 7, 9, 9, 6, 11, 8, 10, 40, 6) !
Penyelesaian
Urutkan data : 6, 6, 7, 8, 8, 9, 9, 10, 11, 40
Karena n=10 genap, maka:
$$\begin{aligned}med &= \frac{1}{2}(X_{(\frac{10}{2})}+X_{(\frac{10}{2}+1)}) \\\\&=\frac{1}{2}(X_{(5)}+X_{(6)}) \\\\&=\frac{1}{2}(8+9) \\\\&=8,5\end{aligned}$$
Nilai median yang diperoleh sebesar 8,5 memberikan gambaran data yang lebih baik dibandingkan rata-rata pada kondisi terdapat data outlier. Nilai ini lebih mencerminkan keadaan data yang sesungguhnya.
Mode (Modus)
Modus menunjukkan nilai amatan yang memiliki frekuensi kemunculan paling banyak. Konsep dari modus paling banyak digunakan pada data kategorik. Konsep ini diterapkan pula pada algoritma machine learning seperti Random Forest untuk pemodelan klasifikasi.
Pada data numerik, modus dapat digunakan pada data diskrit. Sedangkan pada data kontinu, besar kemungkinan data tidak memiliki modus atau memiliki beberapa modus.
Contoh menghitung modus:
- Tentukanlah modus dari kumpulan data berikut (2, 2, 7, 3, 5, 7, 7, 4, 6, 7, 3, 7, 9, 4) !
Penyelesaian
Pada kumpulan data tersebut nilai yang paling sering muncul adalah 7 (sebanyak 5 kali) sehingga modus pada data tersebut = 7
Contoh Data Simulasi
Contoh-contoh berikut ini digunakan untuk menunjukkan bagaimana karakteristik nilai-nilai mean, median dan modus pada berbagai kondisi distribusi data.
Distribusi Simetris
Secara teori, data yang memiliki sebaran simetris akan memiliki karakteristik dimana nilai mean, median dan modus sama.
Kita akan menunjukkan hal tersebut menggunakan data simulasi. Untuk data simulasi yang berdistribusi simetris, akan dibangkitkan 10.000 bilangan acak yang mengikuti sebaran Binomial($n=100$, $p=0.5$). Sebaran binomial dengan peluang sukses 0,5 merupakan sebaran diskret yang simetris sehingga cocok untuk simulasi pada sebaran simetris.
Simulasi ini dikerjakan menggunakan bahasa R. Pada bahasa R, tidak tersedia fungsi untuk mencari nilai modus, oleh karena itu kita juga membuat fungsi sendiri untuk mencari nilai modus.
Sebagai catatan, pada fungsi rbinom, banyaknya ulangan (n) dinotasikan dengan size.
R
# Fungsi menghitung Modus
get.mode <- function(data) {
uniq <- unique(data)
uniq[which.max(tabulate(match(data, uniq)))]
}
set.seed(999)
# membangkitkan 10.000 data yang menyebar binomial(100, 5)
# n : jumlah bilangan acak yang dibangkitkan
# size : jumlah ulangan binomial (notasi n)
# p : peluang sukses setiap ulangan
data.sim <- rbinom(n=10000, size=100, p = 0.5)
mean = mean(data.sim)
median = median(data.sim)
mode = get.mode(data.sim)
# histogram data
hist(data.sim, prob = TRUE, breaks=40, col="#E8E8E8", border = 0.1)
# kurva sebaran binomial(100, 0.5)
axis.x <- seq(0, 100)
axis.y <- dbinom(axis.x, size = 100, p = 0.5)
lines(axis.x, axis.y , lwd = 3, col="red")
abline(v=mean, col="orange", lwd=3, lty=1343)
abline(v=median, col="blue", lwd=3, lty=44)
abline(v=mode, col="black", lwd=3, lty=13)
mean
median
modeOutput
# Output [1] 49.9507 [1] 50 [1] 50
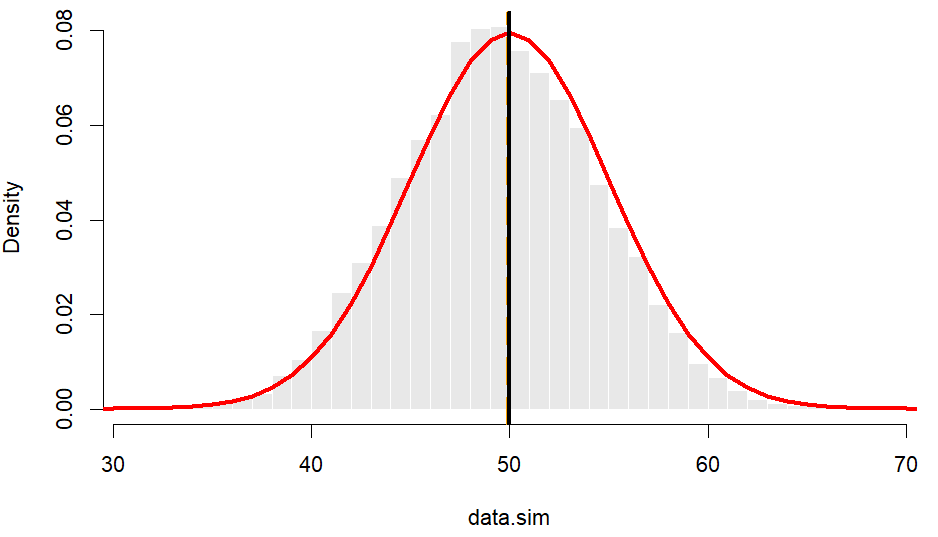

Dari 10.000 data di atas, diperoleh nilai rata-rata = 49,95, median = 50, dan modus = 50. Nilai dari ketiga ukuran pemusatan tersebut dapat dikatakan sama, dimana ketiganya cenderung berada tepat di tengah-tengah kurva sebaran.
Distribusi Menjulur ke Kanan
Data dengan distribusi menjulur ke kanan memiliki karakteristik nilai mean > median > modus. Untuk simulasi, akan digunakan 10.000 data acak yang dibangkitkan dari sebaran Gamma($\alpha=5$, $\beta=3$).
Bilangan acak yang dihasilkan akan kita pangkas menjadi 1 digit desimal. Alasannya jika terlalu banyak desimal, kemungkinan besar kita tidak akan mendapatkan nilai modus, karena semua angka berbeda. Namun, walaupun dilakukan pembulatan dipastikan sebaran yang diperoleh tetap menjulur ke kanan.
R
set.seed(999) data.right <- rgamma(n=10000, 5, 1/3) # untuk keperluan modus bulatkan 1 digit desimal # karena range data tidak terlalu besar data.right <- round(data.right, 1) mean=mean(data.right) median=median(data.right) mode=get.mode(data.right) hist(data.right, prob = TRUE, breaks = 30, border=0.1, col="#E8E8E8") axis.x <- seq(0, 40, .01) axis.y <- dgamma(axis.x, 5, 1/3) lines(axis.x, axis.y , lwd = 3, col="red") abline(v=mean, col="orange", lwd=3, lty=1343) abline(v=median, col="blue", lwd=3, lty=44) abline(v=mode, col="black", lwd=3, lty=13) mean median mode
Output
# Output [1] 14.98589 [1] 13.9 [1] 10.8
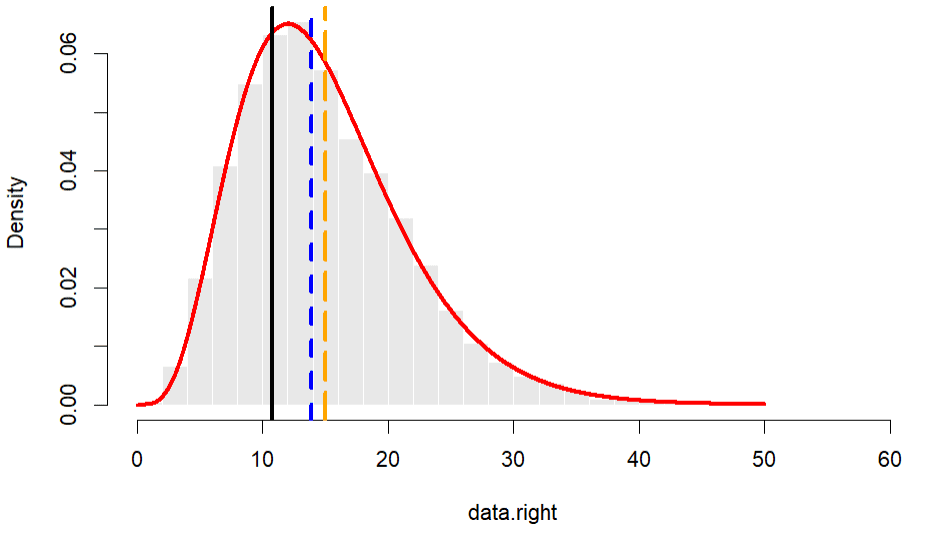

Berdasarkan data simulasi, diperoleh mean = 14,986, median = 13,9 dan modus = 10.8. Melihat interval nilai dari data, perbedaan antara 3 ukuran pemusatan cukup besar khususnya nilai modus. Hasil perhitungan pada data simulasi yang menjulur ke kanan diperoleh nilai mean > median > modus.
Distribusi Menjulur ke Kiri
Sebaran data yang menjulur ke kiri memiliki karakteristik nilai mean < median < modus. Untuk simulasi, akan digunakan 10.000 data acak yang dibangkitkan berdasarkan Beta($\alpha=5$, $\beta=2$). Seperti sebelumnya, kita akan melakukan pembulatan desimal. Untuk data ini kita bulatkan sebanyak 2 desimal, karena selang nilai hanya berkisar antara 0 sampai 1.
R
set.seed(999) data.left <- rbeta(n=10000, 5, 2) # untuk keperluan modus bulatkan 2 desimal # karena rentang nilai hanya dari 0-1 data.left <- round(data.left, 2) mean=mean(data.left) median=median(data.left) mode=get.mode(data.left) hist(data.left, prob = TRUE, breaks = 30, border=0.1, col="#E8E8E8") axis.x <- seq(0, 1, .01) axis.y <- dbeta(axis.x, 5, 2) lines(axis.x, axis.y , lwd = 3, col="red") abline(v=mean, col="orange", lwd=3, lty=1343) abline(v=median, col="blue", lwd=3, lty=44) abline(v=mode, col="black", lwd=3, lty=13) mean median mode
Output
# Output [1] 0.715683 [1] 0.74 [1] 0.8
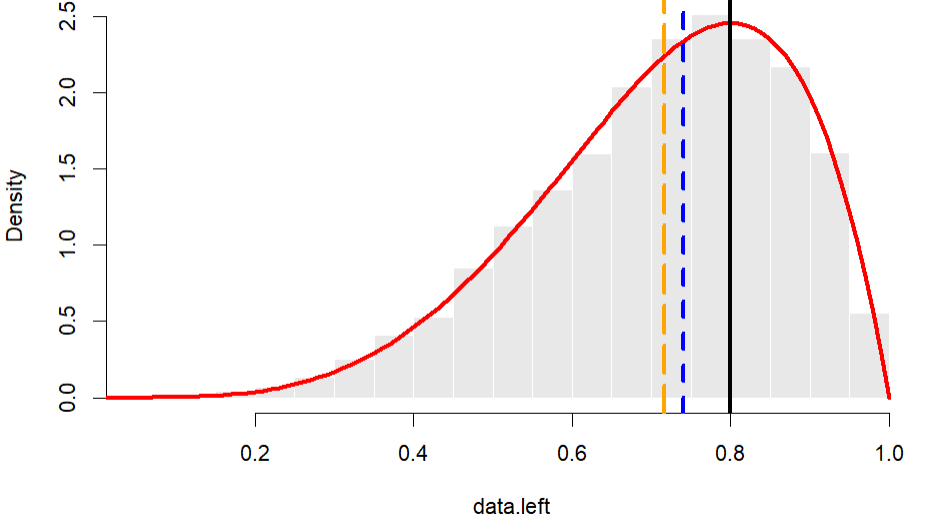

Berdasarkan data simulasi, diperoleh mean = 0,716, median = 0,74 dan modus = 0,8. Dari interval nilai data, dapat kita katakan terdapat perbedaan nilai mean, median dan modus yang cukup besar dimana mean < median < modus, seperti yang diharapkan.
Referensi
Agresti, A., Franklin, C., Klingenberg, B. (2017), Statistics The Art and Science of Learning from Data 4th Editon, Pearson Education.