Asumsi Normalitas pada Regresi Linier dan Miskonsepsi Umum

Dalam regresi linier, ada beberapa asumsi penting yang harus diperhatikan agar hasil analisis valid dan reliable. Salah satu asumsi yang sering dibahas adalah asumsi normalitas. Namun, dalam praktiknya, asumsi ini sering disalahpahami atau diterapkan secara keliru.

Beberapa kali penulis mendengar, sebagian orang menganggap bahwa agar analisis regresi linier dapat dilakukan, data X dan Y harus berdistribusi normal. Kesalahpahaman ini dapat mengarah pada perlakuan yang tidak perlu terhadap data, seperti transformasi yang tidak dibutuhkan, atau bahkan menghindari penggunaan regresi linier meskipun sebenarnya metode tersebut tetap valid.

Sebagai ilustrasi, bayangkan kita memiliki data pengeluaran rumah tangga (Y) yang bersifat skewed, dimana terdapat sebagian orang dengan pengeluaran sangat besar yang menyebabkan data sangat menjulur ke kanan. dan ingin memodelkannya berdasarkan beberapa variabel lain termasuk variabel kategorik.

Setelah dilakukan regresi, kita melakukan analisis terhadap residual dan menemukan bahwa residual tersebut memiliki distribusi mendekati normal. Dalam kasus ini, meskipun data X dan Y tidak normal, model regresi tetap valid untuk inferensi statistik karena residual memenuhi asumsi distribusi normal.

Sebaliknya, bisa saja kita memiliki data Y yang terdistribusi normal, namun residual menunjukkan pola non-acak atau memiliki outlier yang kuat. Hal ini justru dapat mengganggu validitas inferensi regresi. Dengan demikian, penekanan yang benar bukan pada distribusi variabel, tetapi pada sifat residual setelah model diterapkan.

Asumsi normalitas dalam regresi linier klasik merujuk pada distribusi residual atau error term dan tidak merujuk pada distribusi variabel independen (X) maupun dependen (Y). Residual adalah selisih antara nilai observasi aktual dan nilai yang diprediksi oleh model.

Asumsi ini penting dalam konteks:

• Menilai signifikansi koefisien regresi menggunakan uji t.
• Melakukan uji keseluruhan model dengan uji F.
• Membentuk interval kepercayaan terhadap koefisien atau prediksi.

Jika kita hanya fokus pada pembuatan model prediksi dan tidak melakukan inferensi statistik, maka pelanggaran terhadap normalitas residual tidak terlalu menjadi masalah besar.

Gambar berikut ini adalah ilustrasi dari Analisis Regresi Linier Sederhana dengan variabel dependen adalah Revenue dan variabel independen Biaya Iklan. Pada ilustrasi ini, titik BIRU merupakan nilai sebenarnya dari data. Sementara garis berwarna MERAH menunjukkan garis linier dari model regresi. Residual adalah selisih nilai untuk setiap titik tersebut terhadap garis regresi linier.

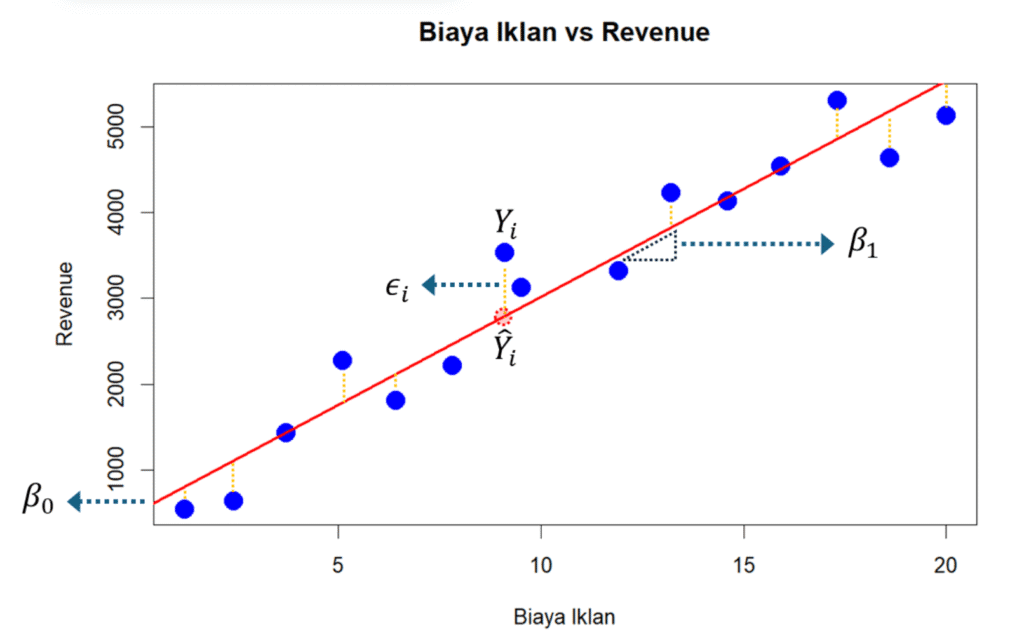
Secara formal residual adalah selisih antara nilai aktual (observasi) dengan nilai yang diprediksi oleh model regresi linier.

Nilai reesidual ($\varepsilon_i$) dihitung sebagai:

$$\varepsilon_i=y_i-\hat{y}_i$$

dengan:

$y_i$: nilai aktual dari variabel dependen untuk observasi ke-i, dan

$\hat{y}_i$: nilai prediksi dari model regresi untuk observasi ke-i, yang dihitung dengan persamaan:

$$\hat{y}_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_p x_{ip}$$

Dalam asumsi klasik regresi linier, error $\varepsilon_i$ diasumsikan:

$$\varepsilon_i \sim \mathcal{N}(0, \sigma^2)$$

Artinya, error harus berdistribusi normal dengan nilai tengah nol dan varians konstan sebesar $\sigma^2$.

Jadi sekali lagi, asumsi normalitas dalam regresi linier merujuk pada distribusi residual atau error term. Residual dari model regresi linier mengikuti distribusi normal dengan nilai tengah nol dan varians konstan

Untuk memeriksa apakah asumsi normalitas pada regresi linier terpenuhi, pendekatan yang disarankan adalah sebagai berikut:

1. Visualisasi Histogram atau Q-Q Plot terhadap residual, guna melihat apakah bentuknya mendekati distribusi normal.
2. Plot residual vs nilai prediksi (fitted values) untuk mendeteksi adanya pola non-acak atau heteroskedastisitas.
3. Uji formal seperti Shapiro-Wilk, Kolmogorov-Smirnov, atau Anderson-Darling terhadap residual. Perlu diingat bahwa uji formal bisa sangat sensitif jika ukuran sampel besar.

Lihat selengkapnya pada artikel berikut: Uji Normalitas Data

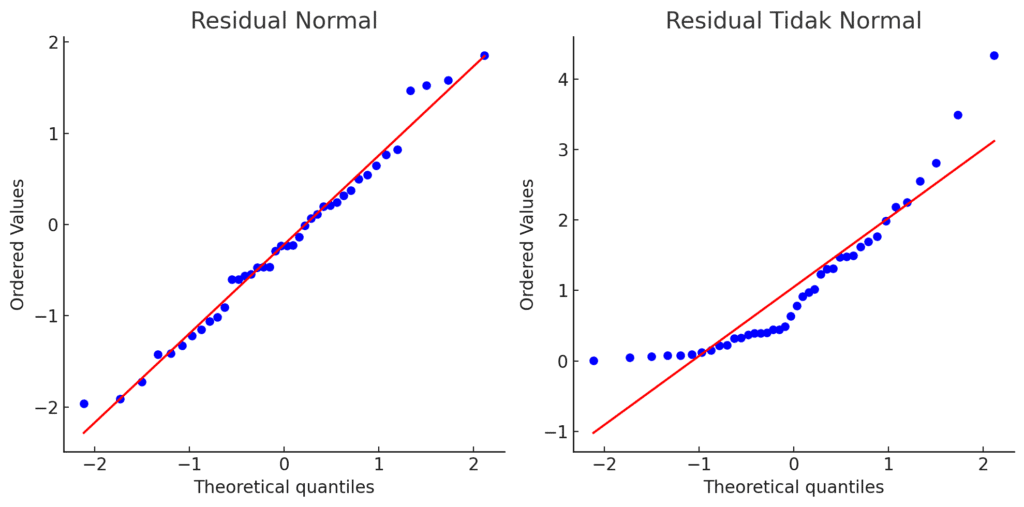
Ingat, dalam konteks analisis regresi linier, pemeriksaan ini dilakukan terhadap nilai residual, bukan terhadap data Y atau X secara langsung.

• Analisis Regresi Linier Berganda dengan Python
• Analisis Regresi Linier Berganda dengan R
• Memahami Teorema Limit Pusat Menggunakan Data Simulasi

• Draper, N. R., & Smith, H. (1998). Applied Regression Analysis (3rd ed.). Wiley.
• Fox, J. (2016). Applied Regression Analysis and Generalized Linear Models (3rd ed.). SAGE Publications.
• Gelman, A., & Hill, J. (2007). Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press.
• Kutner, M. H., Nachtsheim, C. J., Neter, J., & Li, W. (2005). Applied Linear Statistical Models (5th ed.). McGraw-Hill Education.
• Montgomery, D. C., Peck, E. A., & Vining, G. G. (2012). Introduction to Linear Regression Analysis (5th ed.). Wiley.