Memahami Teorema Limit Pusat Menggunakan Data Simulasi

Teorema Limit Pusat, atau Central Limit Theorem (CLT), merupakan salah satu konsep fundamental dalam teori probabilitas dan statistika. Teorema ini menyatakan bahwa semakin besar sampel acak yang diambil, maka distribusi rata-rata dari sampel acak tersebut akan mendekati distribusi normal, tanpa memperhatikan bentuk distribusi asalnya, selama varians populasi terbatas. Karakteristik ini menjadikan CLT sebagai landasan dalam banyak metode statistik, terutama yang berkaitan dengan inferensi pendugaan parameter populasi berdasarkan data sampel.

Secara formal, Teorema Limit Pusat dapat didefinisikan:

Untuk memahami CLT dengan lebih mudah, kita akan menggunakan simulasi. Simulasi membantu kita untuk melihat bagaimana rata-rata dari banyak sampel akan membentuk pola tertentu, meskipun data aslinya mengikuti distribusi yang berbeda-beda.

Pada bagian ini, kita akan mencoba membuat simulasi sederhana. Kita akan membangkitkan data simulasi dari distribusi data tertentu (Distribusi Gamma). Adapun langkah-langkahnya adalah sebagai berikut:

1. Membangkitkan data populasi sintetis (simulasi) sebanyak 10.000 unit yang berasal distribusi $X∼\text{Gamma}(\alpha=2, \beta=1/4)$. Untuk memudahkan deskripsi, kita anggap saja populasi ini merupakan data pendapatan seluruh penduduk di Provinsi A (misal dalam Juta Rupiah) dengan rata-rata yaitu $\alpha/\beta atau 8$ dan varians $\alpha/\beta^2$ yaitu 32
2. Setelah data populasi sintetis dihasilkan, kita menyimulasikan proses penarikan sampel acak dari populasi tersebut. Proses ini kita lakukan dengan jumlah sampel yang berbeda-beda ($n=1$, $n=5$, $n=10$, $n=30$, $n=100$, $n=500$). Untuk setiap ukuran sampel, diulangi sebanyak 1.000 kali.
3. Dari sampel-sampel acak terpilih, untuk setiap ulangan kita hitung rata-rata pendapatannya. Contoh: untuk $n=5$, pada ulangan pertama kita tarik 5 sampel acak kemudian hitung nilai rata-ratanya. Proses ini diulangi sebanyak 1.000 kali, sehingga akan menghasilkan 1.000 nilai rata-rata berbeda untuk setiap ulangannya. Hal yang sama juga kita lakukan untuk ukuran sampel lainnya.
4. Hitung nilai rata-ratanya dan varians-nya dari setiap kumpulan data menurut ukuran sampel
5. Tampilan sebaran nilai rata-rata dalam bentuk histogram

Dengan membandingkan hasil rata-rata dari sampel-sampel itu dengan kurva normal yang ideal, kita bisa melihat bagaimana CLT bekerja. Simulasi ini sangat membantu untuk melihat, meskipun data awal tidak normal, rata-rata dari banyak sampel tetap bisa membentuk distribusi normal.

Langkah pertama yaitu membangkitkan 10.000 data yang mengikuti distribusi $X∼\text{Gamma}(\alpha=2, \beta=1/4)$.

Hasil pembangkitan data dapat disajikan dalam bentuk histogram di bawah ini:

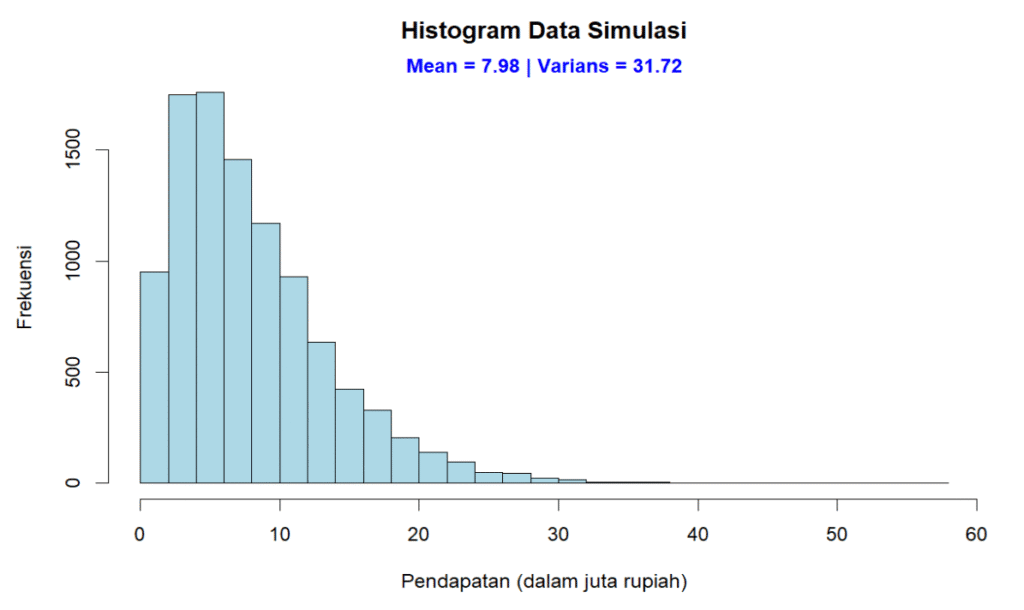
Dari hasil pembangkitan acak tersebut, diperoleh data populasi sintetis yang sangat menjulur ke kanan. Nilai rata-rata populasi adalah sebesar 7,98 dan varians 31,72. Tentu nilainya tidak akan sama persis dengan distribusi teoritisnya yaitu rata-rata sebesar 8 dan varians 32). Namun, pada intinya distribusi data asli untuk populasi sintetis ini sangat jauh dari simetris atau normal.

Dari populasi ini dilakukan penarikan sampel dengan ketentuan yang sudah dibahas sebelumnya. Kemudian hitung nilai rata-ratanya. Hasilnya juga dapat disajikan dalam bentuk histogram.

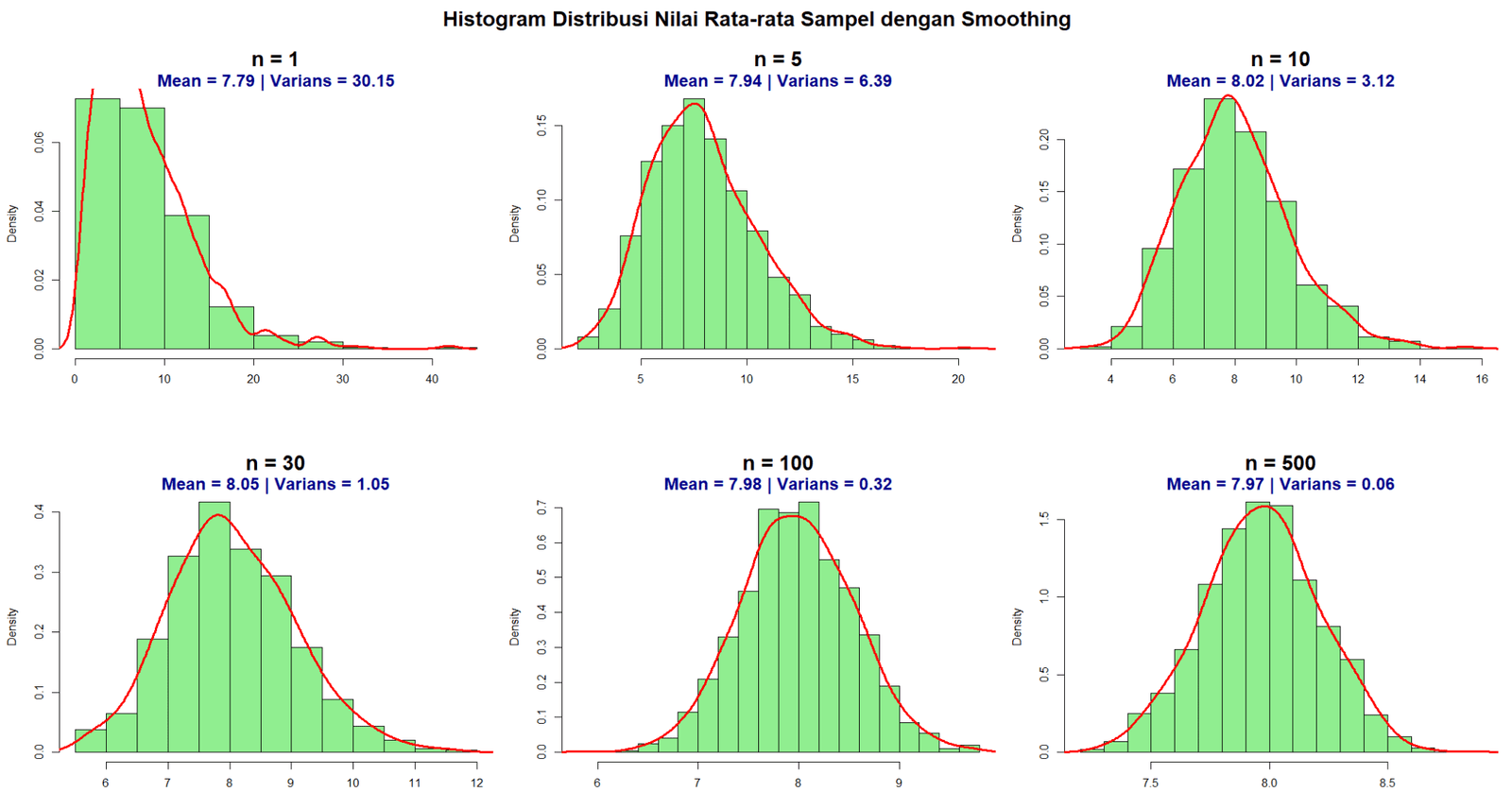
Saat jumlah sampel $n=1$, maka distribusi rata-rata sampel (atau karena hanya 1 data, maka sama dengan distribusi data sampel tersebut) menyerupai distribusi data aslinya. Berikutnya, untuk jumlah sampel $n=5$, distribusi rata-rata sampel masih menjulur, namun tidak begitu besar. Ketika jumlah sampel semakin diperbesar misalnya $n=30$ atau lebih, distribusi nilai rata-ratanya juga semakin menunjukkan bentuk simetris. Hasil ini sejalan dengan teorema limit pusat, semakin besar jumlah sampel maka rata-rata sampel akan mengikuti distribusi Normal.

CLT menyatakan bahwa semakin besar sampel, maka sebaran rata-ratanya memiliki nilai tengah sama dengan data aslinya dan varians sebesar varians data asli dibagi jumlah sampel atau $\bar{X}_n \sim \mathcal{N} \left( \mu, \frac{\sigma^2}{n} \right)$.

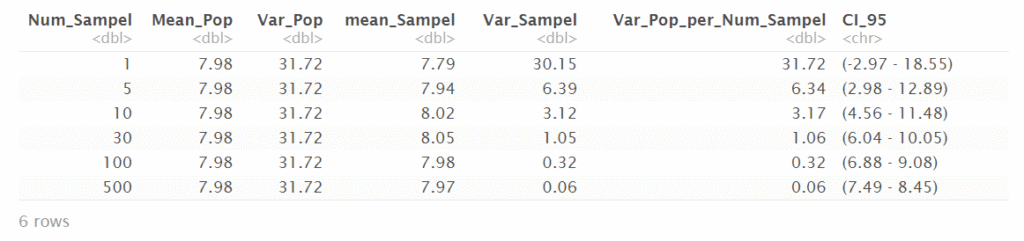
Tabel berikut ini berisi tabulasi hasil simulasi sebelumnya. Dari tabel ini, dapat dilihat bagaimana nilai rata-rata dari rata-rata sampel menurut jumlah sampelnya. Semakin besar jumlah sampel maka rata-ratanya cenderung semakin mendekati rata-rata data asli. Begitu juga untuk nilai varians dari rata-rata sampel tersebut yang nilainya cenderung mendekati nilai varians populasi dibagi jumlah sampel atau semakin kecil. Sebagai akibatnya maka selang kepercayaan untuk estimasi rata-rata akan semakin kecil.

Simulasi ini dapat direproduksi persis seperti yang sudah ditampilkan menggunakan sintaks berikut. Namun, tentunya pembaca dapat mencoba berbagai skenario lainnya. Misalnya, menggunakan distribusi populasi sintetisnya lainnya, atau mencoba dengan skenario ukuran sampel dan ulangan lainnya. Apapun yang dipilih, pembaca akan mendapati bahwa semakin besar jumlah sampel, maka nilai rata-rata sampel tersebut akan menyebar mengikuti distribusi Normal, terlepas dari distribusi data aslinya.

# 1. Bangkitkan data gamma
set.seed(111)  # agar hasil bisa direproduksi

# Membangkitkan 10.000 data mengikuti distribusi Gamma
data_pop <- rgamma(10000, shape = 2, scale = 4)

# 2. Hitung rata-rata dan varians
mean_pop <- mean(data_pop)
var_pop <- var(data_pop)

# 3. Buat histogram
hist(data_pop,
     breaks = 30,
     main = "Histogram Data Simulasi",
     xlab = "Pendapatan (dalam juta rupiah)",
     ylab = "Frekuensi",
     col = "lightblue",
     border = "black")

mtext(text = paste0("Mean = ", round(mean_pop, 2),
                    " | Varians = ", round(var_pop, 2)),
      side = 3, line = 0, cex = 1, col = "blue", font=2 )

set.seed(111)

# 1. Parameter simulasi
ukuran_sampel <- c(1, 5, 10, 30, 100, 500)
n_simulasi <- 1000

# 2. Simulasi penarikan sampel
hasil_simulasi <- lapply(ukuran_sampel, function(n) {
    replicate(n_simulasi, {
    sampel <- sample(data_gamma, size = n, replace = FALSE)
    mean(sampel)
  })
})

# 3. Grid layout
par(mfrow = c(2, 3), mar = c(4, 4, 6, 1))  

# 4. Plot histogram + smoothing
for (i in seq_along(ukuran_sampel)) {
  data_mean <- hasil_simulasi[[i]]
  mean_val <- round(mean(data_mean), 2)
  var_val <- round(var(data_mean), 2)
  
  hist(data_mean,
       breaks = 15,
       main = "",
       xlab = "",
       col = "lightgreen",
       border = "black",
       probability = TRUE)  # skala density untuk overlay

  lines(density(data_mean, bw="SJ" ), col = "red", lwd = 2)  # kurva smoothing merah

  mtext(paste("n =", ukuran_sampel[i]), side = 3, line = 1.5, font = 2, cex = 1.2)
  mtext(paste0("Mean = ", mean_val, " | Varians = ", var_val),
        side = 3, line = 0, font = 2, col = "darkblue", cex = 1)
}

# 5. Judul utama
mtext("Histogram Distribusi Nilai Rata-rata Sampel dengan Smoothing", 
      outer = TRUE, line = -1.5, cex = 1.2, font = 2)

# 1. Hitung mean dan var populasi
mean_pop <- mean(data_gamma)
var_pop <- var(data_gamma)

# 2. Set confidence level
alpha <- 0.05
z_value <- qnorm(1 - alpha / 2)

# 3. Buat tabel ringkasan dari hasil_simulasi
tabel_ringkasan <- do.call(rbind, lapply(seq_along(ukuran_sampel), function(i) {
  n <- ukuran_sampel[i]
  sampel_means <- hasil_simulasi[[i]]
  
  mean_sampel <- mean(sampel_means)
  var_sampel <- var(sampel_means)
  se <- sqrt(var_sampel)
  
  ci_lower <- mean_sampel - z_value * se
  ci_upper <- mean_sampel + z_value * se
  ci_string <- paste0(" (", round(ci_lower, 2), " - ", round(ci_upper, 2), ")")
  
  data.frame(
    Num_Sampel = n,
    Mean_Pop = round(mean_pop, 2),
    Var_Pop = round(var_pop, 2),
    mean_Sampel = round(mean_sampel, 2),
    Var_Sampel = round(var_sampel, 2),
    Var_Pop_per_Num_Sampel = round(var_pop / n, 2),
    CI_95 = ci_string,
    stringsAsFactors = FALSE
  )
}))

# 4. Tampilkan
print(tabel_ringkasan)

Simulasi yang dilakukan terhadap data berdistribusi Gamma menunjukkan bahwa meskipun distribusi asal bersifat menjulur dan tidak normal, distribusi dari rata-rata sampel cenderung mendekati distribusi normal seiring bertambahnya ukuran sampel. Hal ini sesuai dengan Teorema Limit Pusat (CLT) yang menyatakan bahwa distribusi rata-rata dari sampel acak akan mendekati distribusi normal, terlepas dari bentuk distribusi populasi asalnya, asalkan ukuran sampel cukup besar. Selain itu, rata-rata dan varians dari distribusi rata-rata sampel juga mendekati nilai teoritis yang dihitung, dan selang kepercayaan menjadi semakin kecil, menunjukkan meningkatnya presisi estimasi parameter.

1. Wackerly, D., Mendenhall, W., & Scheaffer, R. (2008). Mathematical Statistics with Applications (7th ed.). Belmont, CA: Brooks/Cole.
2. Ross, S. M. (2014). Introduction to Probability and Statistics for Engineers and Scientists (5th ed.). Academic Press.
3. Casella, G., & Berger, R. L. (2002). Statistical Inference (2nd ed.). Duxbury Press.
4. Hogg, R. V., McKean, J., & Craig, A. T. (2018). Introduction to Mathematical Statistics (8th ed.). Pearson.

• Pembangkitan Bilangan Acak pada Bahasa R
• Uji Normalitas Data
• Pengujian Proporsi dan Nilai Tengah Satu Populasi
• Analisis Regresi Linier Berganda dengan R
• Ukuran Pemusatan Data (Central Tendency)