Analisis Data Kategorik dengan Uji Chi-Square

Dalam disiplin ilmu statistik, terutama ketika menangani data kategorik, Uji Chi-Square (Chi-Square Test) merupakan salah satu alat analisis yang esensial. Uji ini dirancang untuk mengevaluasi apakah terdapat hubungan yang signifikan secara statistik antara dua variabel kategorik, atau untuk menentukan apakah distribusi frekuensi observasi menyimpang secara signifikan dari distribusi yang diharapkan.

Secara formal, Uji Chi-Square termasuk dalam kategori uji non-parametrik karena tidak memerlukan asumsi distribusi normal dari populasi. Ada dua varian utama dari uji ini:

1. Chi-Square Goodness of Fit: Menguji kesesuaian distribusi frekuensi observasi dengan distribusi teoritis. Uji ini relevan ketika satu variabel kategorik diperiksa untuk melihat apakah frekuensinya mengikuti pola tertentu yang telah ditentukan.
2. Chi-Square Test of Independence: Digunakan untuk menguji apakah terdapat hubungan atau ketergantungan antara dua variabel kategorik dalam populasi. Diterapkan pada data yang disajikan dalam tabel kontingensi dua arah.

Uji Chi-Square bekerja berdasarkan perbandingan antara frekuensi observasi ($O$) dan frekuensi yang diharapkan ($E$) jika tidak terdapat hubungan antar kategori.

Formula umum yang digunakan adalah:

$$\chi^2 = \sum \frac{(O – E)^2}{E}$$

Di mana:

• $O$ adalah frekuensi aktual yang diamati,
• $E$ adalah frekuensi yang diharapkan berdasarkan asumsi ketidaktergantungan atau distribusi yang telah ditentukan

Semakin besar deviasi antara $O$ dan $E$, semakin besar nilai $\chi^2$, dan semakin besar kemungkinan terdapat hubungan yang signifikan antar variabel.

1. Hipotesis Uji

• $H_0$: Tidak terdapat asosiasi antara variabel (independen)
• $H_1$: Terdapat asosiasi yang signifikan antara variabel

2. Penyusunan Tabel Kontingensi: data disusun ke dalam bentuk tabel dua arah berdasarkan kombinasi kategori antar variabel

3. Perhitungan Frekuensi Harapan (E):

Frekuensi harapan dihitung untuk setiap sel tabel kontingensi berdasarkan total masing-masing baris dan kolom serta total keseluruhan observasi. Nilai ini mewakili jumlah kasus yang diharapkan jika kedua variabel bersifat independen secara statistik.

$$E_{ij} = \frac{(\text{Total baris ke-}i) \times (\text{Total kolom ke-}j)}{\text{Total keseluruhan}}$$

4. Penghitungan Nilai $\chi^2$:

Setelah memperoleh nilai harapan ($E$) untuk setiap sel, hitung deviasi kuadrat antara nilai observasi ($O$) dan nilai harapan ($E$), lalu bagi hasilnya dengan nilai $E$ itu sendiri. Lakukan proses ini untuk seluruh sel dalam tabel kontingensi.

$$\chi^2 = \sum \frac{(O – E)^2}{E}$$

Hasil akhir dari penjumlahan seluruh sel akan menghasilkan nilai statistik, yang kemudian dibandingkan dengan nilai kritis atau digunakan untuk menghitung p-value.

5. Penentuan Derajat Kebebasan (df):

$$df = (r – 1) \times (c – 1)$$

di mana $r$ adalah jumlah baris dan $c$ jumlah kolom.

6. Evaluasi Statistik Uji:

Bandingkan nilai $\chi^2$ dengan nilai kritis dari distribusi pada $df$ tertentu dan tingkat signifikansi (misalnya $\alpha = 0,05$). Atau, hitung p-value dan bandingkan dengan $\alpha$.

7. Kesimpulan:

Jika p-value $< \alpha$, tolak $H_0$ ; terdapat bukti signifikan adanya asosiasi

Jika p-value $\geq \alpha$, gagal menolak $H_0$

Seorang peneliti ingin mengevaluasi apakah preferensi jenis minuman (kopi, teh, jus) bergantung pada jenis kelamin. Data dikumpulkan dan disusun dalam bentuk tabel kontingensi sebagai berikut:

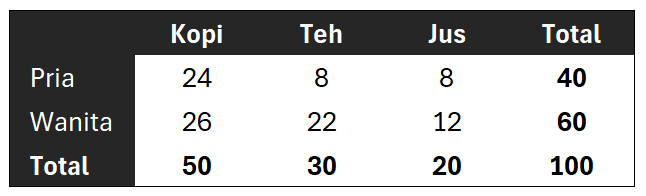
Dari tabel kontingensi tersebut, kemudian dihitung frekuensi harapan untuk masing-masing kombinasi. Misalnya untuk kombinasi Pria dan Kopi dihitung dengan formula $E_{pk}=\frac{40×50}{100}=20$. Begitu juga untuk kombinasi lainnya.

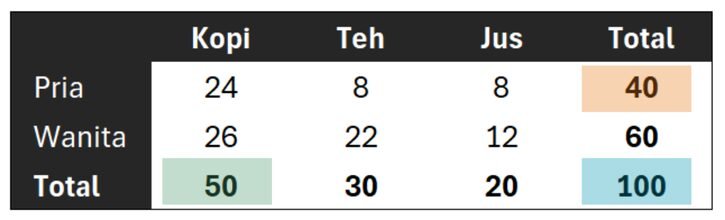
Hasil perhitungan frekuensi harapan (E) untuk masing-masing sel adalah:

• Pria – Kopi: $E_{pk}=\frac{40×50}{100}=20$
• Pria – Teh: $E_{pt}=\frac{40×30}{100}=12$
• Pria – Jus: $E_{pj}=\frac{40×20}{100}=8$
• Wanita – Kopi: $E_{wk}=\frac{60×50}{100}=30$
• Wanita – Teh: $E_{pt}=\frac{60×30}{100}=18$
• Wanita – Jus: $E_{pj}=\frac{60×20}{100}=12$

Selanjutnya hitung nilai $\chi_2$:

• Pria – Kopi: $=\frac{(24 – 20)^2}{20} = \frac{16}{20} = 0.8$
• Pria – Teh: $\frac{(8 – 12)^2}{12} = \frac{16}{12} \approx 1.33$
• Pria – Jus: $=\frac{(8 – 8)^2}{8} = 0$
• Wanita – Kopi: $\frac{(26 – 30)^2}{30} = \frac{16}{30} \approx 0.53$
• Wanita – Teh: $\frac{(22 – 18)^2}{18} = \frac{16}{18} \approx 0.89$
• Wanita – Jus: $\frac{(12 – 12)^2}{12} = 0$

$\chi^2 = 0,8 + 1,33 + 0 + 0,53 + 0,89 + 0 = 3,55$

Pada kasus ini nilai df = (2 – 1)(3 – 1) = 2, sehingga selanjutnya kita cek apakah statistik uji $\chi^2$ lebih besar dari nilai kritisnya atau tidak.

Dengan menggunakan software seperti Ms. Excel, dengan $\alpha=0,05$ dan derajat bebas $2$ diperoleh nilai kritisnya adalah $5,991$. Karena nilai $\chi^2=3,55$ lebih kecil dari $5,991$ maka keputusannya adalah tidak tolak $H_0$. Kesimpulan yang dapat diambil yaitu pada tingkat kepercayaan 95 persen, belum cukup bukti untuk menyatakan adanya perbedaan preferensi minuman yang signifikan antara pria dan wanita.

Cara lainnya yaitu menghitung nilai probabilitas (p-value) untuk $\chi^2=3,55$ dengan derajat bebas $2$. Hasil perhitungan menunjukkan p-value sebesar $0,1695$. Karena p-value lebih besar dari $\alpha$ maka keputusannya sama yaitu tidak tolak $H_0$.

Sebagai salah satu teknik analisis utama dalam analisis data kategorik, Uji Chi-Square memberikan kerangka kerja yang kuat untuk menguji hipotesis independensi atau kesesuaian distribusi. Dengan pemahaman menyeluruh terhadap mekanisme dan interpretasi hasilnya, kita dapat memanfaatkan uji ini secara efektif dalam berbagai konteks riset kuantitatif.

Untuk eksplorasi lebih lanjut, praktikkan analisis Chi-Square menggunakan perangkat lunak seperti JASP, R, Python (scipy.stats), atau bahkan spreadsheet seperti Microsoft Excel untuk mempercepat proses perhitungan dan menyajikan hasil dalam format tabulasi yang lebih informatif.

• Pengujian Proporsi dan Nilai Tengah Satu Populasi
• Uji Normalitas Data
• Skala Pengukuran Data: Fondasi Analisis Statistik