Analisis Regresi Linier Berganda dengan Python


Analisis regresi linier berganda adalah analisis statistika inferensia yang digunakan untuk memodelkan hubungan antara satu variabel dependen (respon) dengan dua atau lebih variabel independen (prediktor).
Pada tutorial ini, kita akan mempraktikan tahap demi tahap analisis regresi berganda menggunakan bahasa Python. Tutorial ini fokus pada analisis regresi berganda untuk inferensia, sehingga tidak akan membahas pada tahapan melatih model dengan pembagian data latih dan data uji, validasi silang ataupun melakukan prediksi data baru.
[Tutorial ini juga tersedia dalam Bahasa R: Analisis Regresi Linier Berganda dengan R]
Penyiapan Data
Data yang akan digunakan dalam tutorial ini adalah data Indeks Pembangunan Manusia (IPM) Tahun 2018 dari 119 Kabupaten/Kota di Pulau Jawa. Terdapat 16 kolom (selain kolom ID) dimana Nilai IPM akan menjadi peubah respon dan 15 lainnya sebagai peubah penjelas (merupakan indikator hasil agregasi data Potensi Desa 2018) dan seluruhnya bertipe numerik. Keterangan masing-masing kolom adalah sebagai berikut:
ID: Kode Kab/Kota (4 digit Kode BPS)IPM: Nilai IPMPR_NO_LIS: Proporsi keluarga yang tidak menggunakan listrik baik PLN maupun non-PLNPR_SAMPAH: Proporsi desa/kelurahan pada kabupaten/kota dimana sebagian besar warganya membuang sampah di sungai/saluran irigasi/danau/laut serta got/selokan dan lainnyaPR_TINJA: Proporsi desa/kelurahan pada kabupaten/kota dimana tempat pembuangan akhir tinja sebagian besar warganya adalah sawah/kolam/sungai/danau/laut atau pantai/tanah lapang/kebun, lubang tanah dan lainnyaPR_MKM_SUNGAI: Proporsi desa/kelurahan di kabupaten/kota yang memiliki pemukiman di bantaran sungaiPR_SUNGAI_LMBH: Proporsi desa/kelurahan di kabupaten/kota yang memiliki sungai yang tercemar limbahPR_KUMUH: Proporsi desa/kelurahan di kabupaten/kota yang memiliki pemukiman kumuhPRA_1000: Jumlah PAUD dan TK per 1000 pendudukSD_1000: Jumlah SD/MI per 1000 pendudukSM_1000: Jumlah sekolah menengah (SMP/MTs, SMA/MA, SMK) per 1000 pendudukRS_PKS_PDK_1000: Jumlah rumah sakit, puskesmas, puskesmas pembantu, poliklinik, praktek dokter per 1000 pendudukLIN_BID_POS_1000: Jumlah rumah bersalin, praktek bidan, posyandu, polindes per 1000 pendudukAPT_OBT_1000: Jumlah apotek dan toko obat per 1000 pendudukDOK_DRG_1000: Jumlah dokter dan dokter gigi per 1000 pendudukBID_1000: Jumlah bidan per 1000 pendudukGZ_BURUK_1000: Jumlah kejadian gizi buruk per 1000 penduduk
Python
# Membaca data import pandas as pd import numpy as np url = "https://raw.githubusercontent.com/sainsdataid/dataset/main/data_ipm_jawa_2018.csv" data = pd.read_csv(url) # Melihat struktur data print(data.info()) # Menghapus kolom id karena tidak diperlukan data = data.drop(columns='id')
# OUTPUT <class 'pandas.core.frame.DataFrame'> RangeIndex: 119 entries, 0 to 118 Data columns (total 17 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 id 119 non-null int64 1 ipm_2018 119 non-null float64 2 PR_NO_LIS 119 non-null float64 3 PR_SAMPAH 119 non-null float64 4 PR_TINJA 119 non-null float64 5 PR_MKM_SUNGAI 119 non-null float64 6 PR_SUNGAI_LMBH 119 non-null float64 7 PR_KUMUH 119 non-null float64 8 PRA_1000 119 non-null float64 9 SD_1000 119 non-null float64 10 SM_1000 119 non-null float64 11 RS_PKS_PDK_1000 119 non-null float64 12 LIN_BID_POS_P_1000 119 non-null float64 13 APT_OBT_1000 119 non-null float64 14 DOK_DRG_1000 119 non-null float64 15 BID_1000 119 non-null float64 16 GZ_BURUK_1000 119 non-null float64 dtypes: float64(16), int64(1) memory usage: 15.9 KB
Analisis Data Eksploratif
Ringkasan Data
Sebelum masuk ke tahap pemodelan, sangat disarankan untuk melakukan eksplorasi data untuk lebih memahami kondisi data. Terdapat beberapa hal yang akan kita lakukan dan dimulai dengan mengecek ringkasan data. Hasil ringkasan data, memberikan sedikit gambaran bagaimana karakteristik masing-masing peubah. Misalkan untuk peubah respon kita yaitu ipm_2018, nilai terkecil pada data adalah 61,00 dan nilai terbesar adalah 86,11 denga nilai rataan adalah 71,23.
Kita juga perlu memastikan tidak ada data hilang. Jika ternyata terdapat data hilang, maka perlu dilakukan penanganan, entah dengan menghapus baris, kolom atau melakukan imputasi. Pada dataset yang kita gunakan kebetulan tidak terdapat data hilang sehingga dapat dilanjutkan dengan pengecekan lainnya.
Python
# Melihat summary data
print(data.describe())
# Pengecekan missing value
cek_na = data.isna().sum()
# Merubah menjadi dataframe agar lebih rapi
cek_na_df = pd.DataFrame({
'Variabel': cek_na.index,
'Jumlah NA': cek_na.values
})
print(cek_na_df)# OUTPUT
ipm_2018 PR_NO_LIS PR_SAMPAH ...
count 119.000000 119.000000 119.000000 ...
mean 71.980504 0.001514 0.074437 ...
std 5.459299 0.003732 0.083234 ...
min 61.000000 0.000000 0.000000 ...
25% 67.905000 0.000000 0.000000 ...
50% 71.230000 0.000131 0.049822 ...
75% 74.915000 0.001023 0.105149 ...
max 86.110000 0.024648 0.358896 ...
Variabel Jumlah NA
0 ipm_2018 0
1 PR_NO_LIS 0
2 PR_SAMPAH 0
3 PR_TINJA 0
.. ... .
14 BID_1000 0
15 GZ_BURUK_1000 0Boxplot Sebaran Variabel Numerik
Semua variabel pada daset bertipe numerik, sehingga kita dapat membuat boxplot untuk masing-masing variabel. melalui boxplot kita dapat memperoleh informasi bagaimana data menyebar dan juga dapat digunakan unutk mengidentifikasi keberadaan outlier.
Dengan memanfaatkan subplots kita dapat membuat sekaligus semua boxplot dengan beberapa baris kode saja. Hasil visualisasi boxplot di bawah ini menunjukkan bahwa masing-masing variabel memiliki pola sebaran yang beragam. Sebagian besar terdapat titik-titik data yang diindikasikan sebagai outlier. Tentunya hal ini perlu dilihat dengan lebih seksama. Jika memang kondisi tersebut sesuatu yang wajar berarti tidak ada masalah. Namun jika dianggap ada yang tidak sesuai maka perlu dilakukan pengecekan dan penanganan kondisi tersebut.
Di sini, kita akan menganggap semua kondisi ini sesuai dengan fakta lapangan dan tidak akan melakukan penanganan apapun.
Python
import matplotlib.pyplot as plt
import seaborn as sns
# Mengatur ukuran grid
ncols = 4
nrows = (len(data.columns) // ncols) + (len(data.columns) % ncols > 0)
# Membuat plot
fig, axes = plt.subplots(nrows=nrows, ncols=ncols, figsize=(12, 8))
axes = axes.flatten()
for i, var in enumerate(data.columns):
sns.boxplot(data=data[var], ax=axes[i], color="orange", orient="h", width=0.5)
plt.tight_layout()
plt.show()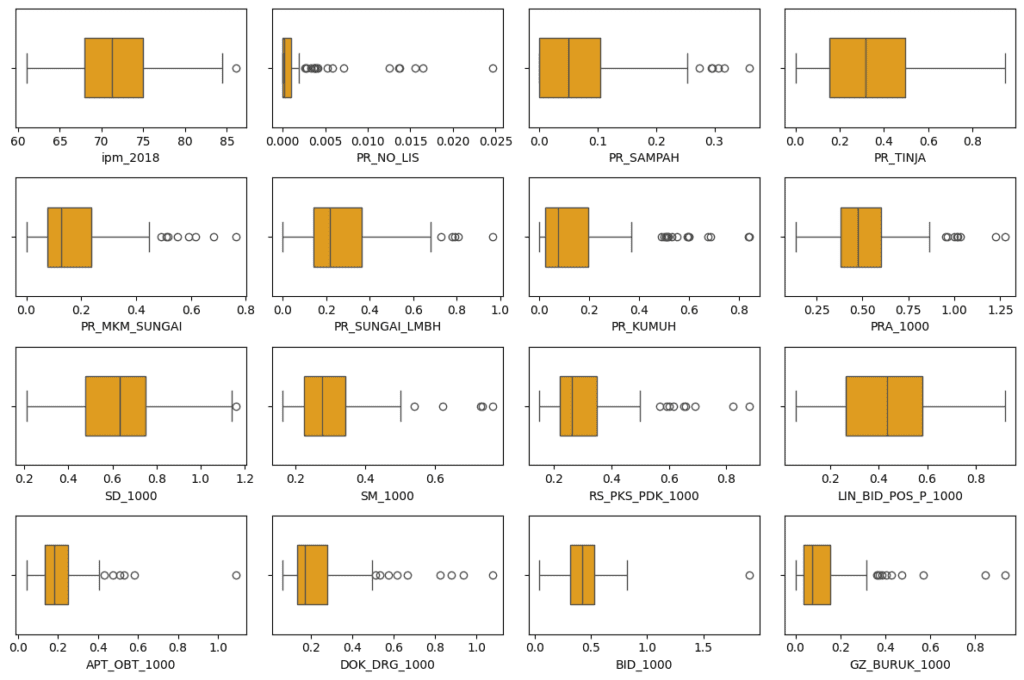

Boxplot Sebaran nilai masing-masing peubah (gambar: penulis)
Korelasi Antar Variabel
Melihat koerelasi antar variabel merupakan bagian penting. Hal ini dapat menjadi indikasi awal apakah terdapat kondisi multikolinieritas pada data yang kita miliki. Tentunya lebih jauh kita dapat melihat nilai VIF untuk lebih meyakinkan.
Dari plot korelasi berikut, terlihat beberapa kolom memiliki nilai korelasi yang tinggi, sehingga mungkin akan terdapat kondisi multikolinieritas. Adapun untuk korelasi antara peubah penjelas dengan peubah respon, terlihat beberapa peubah memiliki korelasi yang cukup tinggi seperti DOK_DRG_1000, SD_1000, PR_TINJA dan sebagainya.
Selain itu, korelasi ini dapat menjadi informasi awal untuk melihat bagaimana hubungan antara setiap variabe penjelas dengan variabel respon. Sebagai contoh, cukup mengejutkan melihat korelasi beberapa data yang tampak agak “aneh”. Misal, korelasi SD_1000 atau SM_1000 dengan nilai IPM memiliki korelasi yang negatif. Semakin banyak SD_1000 maka nilai IPM di Kabupaten/Kota tersebut semakin rendah. Sebaliknya Korelasi PR_KUMUH serta PR_SUNGAI_LMBH terhadap nilai IPM bernilai positif. Dimana artinya, semakin tinggi proporsi pemukiman kumuh, atau proporsi sungai yang tercemar limbah maka nilai IPM di kabupaten tersebut cenderung lebih tinggi juga.
Tentunya banyak hal yang mungkin menyebabkan kondisi tersebut terjadi, dan tentunya perlu dikaji secara lebih komprehensif. Namun untuk tulisan singkkat ini, kita tidak akan melihat jauh di luar teknis analisis regresi.
Python
# Menghitung korelasi antar kolom
corr_matrix = data.corr().round(2)
# Membuat mask untuk menghapus segitiga atas
mask = np.triu(np.ones_like(corr_matrix, dtype=bool))
# Membuat plot korelasi
plt.figure(figsize=(10, 8))
sns.heatmap(
corr_matrix,
annot=True,
fmt=".2f",
mask=mask,
cmap="coolwarm",
linewidths=0.5,
linecolor="white",
)
plt.xticks(rotation=45, ha="right", fontsize=10)
plt.yticks(fontsize=10)
plt.tight_layout()
plt.show()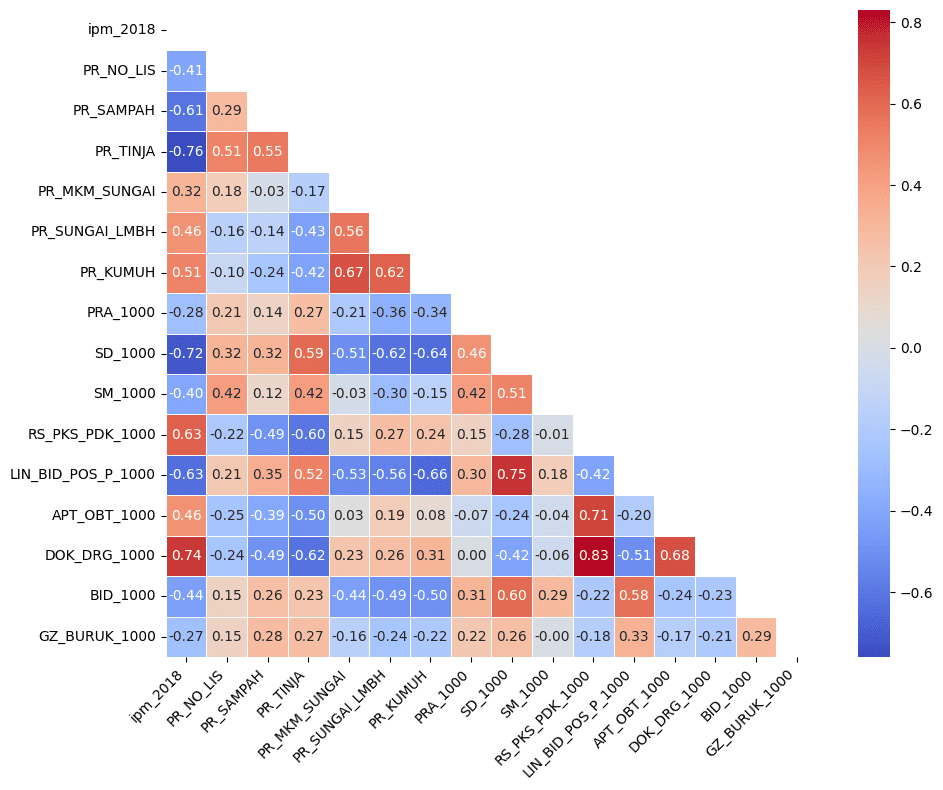

Plot korelasi antar variabel (gambar: penulis)
Model Regresi
Jika kondisi data sudah ‘clean’, maka kita dapat masuk ke tahap pembuatan model regresi linier berganda. Library statsmodels menyediakan fungsi OLS yang dapat kita gunakan secara cepat dan sederhana untuk model regresi linier. Terdapat beberapa library lain, namun untuk saat ini kita hanya akan menggunakan fungsi OLS saja. Parameter yang perlu ditentukan pada fungsi OLS adalah variabel dependen (y) dan variabel independen (X). Variabel independen harus ditambahkan konstanta menggunakan add_constant dari statsmodels.
Output dari model dapat dilihat dengan menggunakan metode summary.
Python
import statsmodels.api as sm # Memisahkan variabel independen (X) dan dependen (y) X = data.drop(columns=['ipm_2018']) y = data['ipm_2018'] # Menambahkan konstanta ke variabel independen X = sm.add_constant(X) # Melatih model regresi linear model_reg = sm.OLS(y, X).fit() # Menampilkan ringkasan output model print(model_reg.summary())
# OUTPUT
OLS Regression Results
==============================================================================
Dep. Variable: ipm_2018 R-squared: 0.847
Model: OLS Adj. R-squared: 0.825
Method: Least Squares F-statistic: 38.14
Date: Sat, 20 Jul 2024 Prob (F-statistic): 3.48e-35
Time: 14:41:51 Log-Likelihood: -258.46
No. Observations: 119 AIC: 548.9
Df Residuals: 103 BIC: 593.4
Df Model: 15
Covariance Type: nonrobust
======================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------
const 77.6934 1.616 48.089 0.000 74.489 80.898
PR_NO_LIS -54.1662 72.840 -0.744 0.459 -198.628 90.295
PR_SAMPAH -12.3238 3.342 -3.687 0.000 -18.952 -5.696
PR_TINJA -3.8587 1.637 -2.358 0.020 -7.104 -0.613
PR_MKM_SUNGAI -0.3064 2.239 -0.137 0.891 -4.746 4.133
PR_SUNGAI_LMBH -0.0665 1.710 -0.039 0.969 -3.457 3.324
PR_KUMUH 1.1478 1.876 0.612 0.542 -2.572 4.868
PRA_1000 -1.4733 1.359 -1.084 0.281 -4.169 1.223
SD_1000 -8.4772 2.239 -3.785 0.000 -12.919 -4.036
SM_1000 -3.5570 2.852 -1.247 0.215 -9.214 2.100
RS_PKS_PDK_1000 5.0663 3.635 1.394 0.166 -2.142 12.275
LIN_BID_POS_P_1000 2.9505 2.038 1.448 0.151 -1.091 6.992
APT_OBT_1000 -7.7274 2.887 -2.677 0.009 -13.452 -2.002
DOK_DRG_1000 13.5001 2.481 5.441 0.000 8.579 18.421
BID_1000 -2.2206 1.528 -1.453 0.149 -5.251 0.810
GZ_BURUK_1000 0.6344 1.567 0.405 0.686 -2.472 3.741
==============================================================================
Omnibus: 0.704 Durbin-Watson: 1.636
Prob(Omnibus): 0.703 Jarque-Bera (JB): 0.336
Skew: 0.080 Prob(JB): 0.845
Kurtosis: 3.206 Cond. No. 563.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Output yang disajikan di atas menampilkan berbagai nilai-nilai yang biasa diintepretasikan dari hasil pemodelan. Beberapa di antaranya adalah:
Koefisien Regresi
Nilai ini menunjukkan nilai koefisien regresi ($\hat{\beta_i}$) untuk masing-masing variabel. Misalkan, untuk variabel PR_NO_LIS memiliki nilai koefisien -54,166 dan untuk DOK_DRG_1000 bernilai 13,50. Tanda positif menunjukkan hubungan yang positif antara variabel penjelas dan responnya, sebaliknya tanda negatif menunjukkan hubungan negatif antara keduanya.
Statistik uji t
Komponen ini (P>|t|) menunjukkan variabel penjelas mana saja yang signifikan. Jika nilai p-value lebih kecil dari nilai $\alpha$ tertentu, misal 0,05 maka peubah tersebut siginifikan pada tingkat keyakinan $100- $\alpha$. Sebagai contoh menggunakan $\alpha=0.05$, nilai p-value untuk PR_SAMPAH adalah 0,000 < 0,05 sehingga termasuk variabel yang signifikan. Hal ini juga dapat dilihat melalui selang kepercayaan nilai koefisiennya yang memiliki batas-batas nilai dengan tanda yang sama yaitu -18,952 sampai -5,696. Sebaliknya, variabel PR_KUMUH memiliki nilai p-value sebesar 0,542 > 0,05 sehingga termasuk variabel yang tidak signifikan. Hasil ini dapat dilihat juga berdasarkan selang kepercayaan nilai keofisiennya yang berada antara -2,572 sampai 4,868 (mengandung nilai 0).
Statistik uji F
Jika statistik uji $t$ menunjukkan secara parsial signifikansi masing-masing variabel, maka statistik uji $F$ mengukur signifikansi model secara keseluruhan. Pada contoh ini, nilai statistik F adalah 38,14 dengan p-value $≈$ 0 ($p-value: = 3.48e-35$) menunjukkan model signifikan (bahkan dengan tingkat kesalahan yang sangat kecil, misal $alpha=0.00001$ atau lebih kecil lagi) . Dengan kata lain, dapat disimpulkan bahwa terdapat setidaknya 1 variabel penjelas yang signifikan (atau setidaknya terdapat satu $i$ untuk $\text{i=1,2…,15}$ di mana nilai $\beta_i\neq0$. Hal ini tentunya juga sudah sesuai dengan hasil uji parsial sebelumnya.
Koefisien Determinasi ($R^2$)
Nilai $R^2$ menunjukkan besarnya keragaman pada variabel respon yang dapat dijelaskan oleh variabel penjelas. Pada contoh ini nilai $R^2=0.847$ artinya variabel-variabel penjelas pada model mampu menjelaskan sekitar 84,7 persen keragaman pada nilai IPM.
Adjusted $R^2$
Nilai adjusted $R^2$ adalah nilai $R^2$ yang diberikan penalti berupa banyaknya variabel penjelas yang digunakan. Ukuran ini biasanya digunakan saat membandingkan kinerja antar model dengan tetap mempertimbangkan kompleksitas model. Model yang lebih sederhana akan di penalti lebih kecil dibandingkan model yang kompleks. Sebagai contoh, Model A dengan 15 variabel memiliki nilai $R^2=0.84$ dan model B dengan hanya 5 variabel memiliki niai $R^2=0.82$. Jika dihitung nilai adjusted $R^2$, bisa jadi Model B akan memberikan nilai yang lebih tinggi dibandingkan Model A. Hal ini dapat dimaknai, dengan pengurangan kompleksitas model yang besar (dari 15 variabel menjadi hanya 5 variabel) model tetap memiliki kinerja yang baik dan hanya sedikit saja mengurangi $R^2$ (dari 0,84 menjadi 0,82). Jika terjadi situasi seperti ini mungkin kita akan lebih cenderung memilih model B dibandingkan A.
Pengecekan Asumsi
Normalitas
Analisis regresi linier berganda mengasumsikan bahwa residual (perbedaan antara nilai yang diamati dan nilai yang diprediksi) terdistribusi secara normal. Asumsi ini dapat dinilai dengan memeriksa histogram atau Q-Q plot dari residual, atau melalui uji statistik seperti uji Kolmogorov-Smirnov, Shapiro-Wilk dan sebagainya.
Pada hasil qq plot maupun uji formal menggunakan uji K-S (tidak tolak $H_0$ karena $p-value > 0,05$), residual model memenuhi asumsi normalitas yaitu menyebar $\text{Normal}(0, \sigma^2)$.
Python
from scipy import stats
# Mendapatkan residual dari model
model_res = model_reg.resid
mean_res = round(np.mean(model_res), 4)
sd_res = round(np.std(model_res), 4)
print("Nilai tengah residual:", mean_res)
print("Simpangan baku residual:", sd_res)
# Membuat QQ plot dari residual
stats.probplot(model_res, dist="norm", plot=plt)
plt.title("QQ-Plot")
plt.xlabel("Theoritical Quantiles")
plt.ylabel("Quantiles of sample data")
plt.show()
# Melakukan uji Kolmogorov-Smirnov pada residual
ks_result = stats.kstest(model_res, "norm", args=(mean_res, sd_res))
print(ks_result)# OUTPUT
Nilai tengah residual: 0.0
Simpangan baku residual: 2.1234
KstestResult(statistic=0.04931017440679053,
pvalue=0.9205685084687579,
statistic_location=0.07301368423065924,
statistic_sign=1)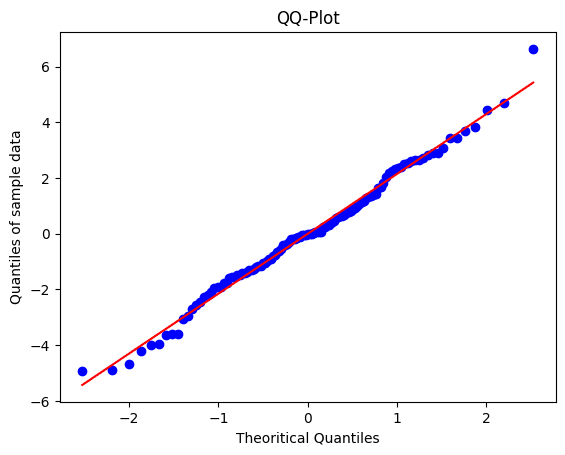

Homoskedastisitas
Ragam dari residual harus konsisten di seluruh tingkat variabel penjelas. Scatterplot dari residual versus nilai prediksi tidak boleh menampilkan pola yang terlihat, seperti distribusi berbentuk kerucut ataupun corong, yang artinya menunjukkan heteroskedastisitas. Jika diperlukan, terdapat pula uji-uji statistik yang dgunakan untuk mengecek asumsi ini seperti uji Breusch-Pagan, uji White dan sebagainya. Jika terdapat kondisi heteroskedastisitas, maka dapat juga dilakukan penanganan melalui transformasi data.
Pada kasus ini, berdasarkan uji BP (tidak tolak $H_0$ karena $p-value > 0,05$) dan plot sebaran nilai residual terlihat relatif menyebar acak untuk setiap nilai prediksi dan tidak ada kecenderungan membentuk pola kerucut. Dengan demikian dapat dikatakan tidak terdapat heteroskedastisitas.
Python
from statsmodels.stats.diagnostic import het_breuschpagan
# Melakukan uji Breusch-Pagan
bp_test = het_breuschpagan(model_res, model_reg.model.exog)
bp_test_result = dict(
zip(["Lagrange multiplier statistic", "p-value", "f-value", "f p-value"], bp_test)
)
print(bp_test_result)
# Membuat plot residual vs nilai prediksi
plt.scatter(model_reg.fittedvalues, model_res, color='red', s=30)
plt.axhline(y=0, color='blue', linestyle='--')
plt.xlabel('Fitted Values')
plt.ylabel('Residuals')
plt.title('Residuals vs Fitted Values')
plt.show()# OUTPUT
{'Lagrange multiplier statistic': 15.259972345570015,
'p-value': 0.4328581329533153,
'f-value': 1.0100743734967204,
'f p-value': 0.45101887238802657}
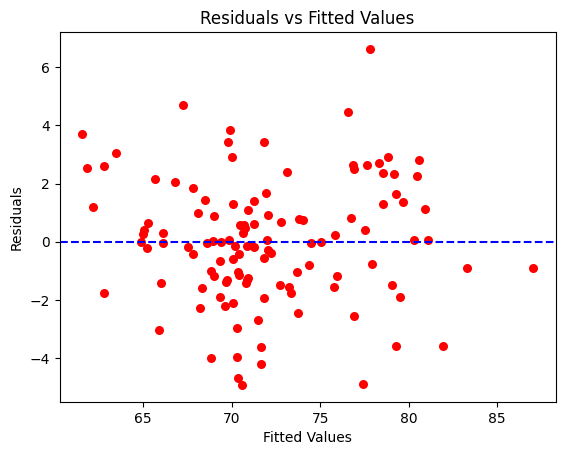

Plot residual vs fitted value (gambar: penulis)
Non-Multikolinieritas
Multikolinieritas (Ini sebenarnya bukanlah sebuah asumsi) merupakan masalah yang perlu ditangani. Analisis model dengan keberadaan multikolinieritas bisa menjadi tidak tepat. Ragam penduga menjadi lebih besar sehingga juga akan memperlebar selang kepercayaannya. Dampak dari selang kepercayaan yang lebih lebar adalah uji dapat menjadi tidak signifikan meskipun seharusnya variabel tersebut memiliki pengaruh kuat. Hal ini juga tidak menutup kemungkinan sampai menyebabkan penduga keofisien menjadi berubah tanda (positif menjadi negatif atau sebaliknya). Jika terjadi demikian tentu hasil analisis menjadi tidak reliable untuk digunakan.
Keberadaan masalah multikolinieritas dapat dilihat dengan cara berikut:
- Matriks korelasi, di mana batas koefisien korelasi 0,80 dapat menjadi ‘warning’. Pada bagian sebelumnya, kita sudah menyajikan matriks korelasi dan menunjukkan beberapa variabel penjelas dengan korelasi cukup tinggi.
- Variance Inflation Factor (VIF), dengan nilai VIF > 10 menunjukkan adanya masalah multikolinieritas.
Python
from statsmodels.stats.outliers_influence import variance_inflation_factor # Menghitung VIF untuk setiap variabel dalam model vif_data = pd.DataFrame() vif_data['Variable'] = X.columns vif_data['VIF'] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])] print(vif_data)
# OUTPUT
Variable VIF
0 const 59.630453
1 PR_NO_LIS 1.674004
2 PR_SAMPAH 1.752889
3 PR_TINJA 3.883222
4 PR_MKM_SUNGAI 2.519156
5 PR_SUNGAI_LMBH 2.248597
6 PR_KUMUH 2.945363
7 PRA_1000 1.840095
8 SD_1000 4.638975
9 SM_1000 2.323137
10 RS_PKS_PDK_1000 5.283640
11 LIN_BID_POS_P_1000 3.867567
12 APT_OBT_1000 3.014481
13 DOK_DRG_1000 4.545848
14 BID_1000 2.377227
15 GZ_BURUK_1000 1.272896Jika terdapat masalah multikolinieritas tersebut kita mungkin perlu mengeluarkan salah satu atau lebih variabel-variabel dengan korelasi yang kuat.
Berdasarkan hasil di atas, ternyata tidak terdapat indikasi masalah multikolinieritas antar variabel penjelas (abaikan nilai untuk konstanta). Hal ini dapat meyakinkan kita bahwa analisis regresi linier berganda yang kita lakukan sudah memenuhi asumsi-asumsi serta tidak terdapat masalah yang dapat mengganggu hasil dan interpretasinya.
Referensi
- Agresti, A., Franklin, C., Klingenberg, B. 2018. Statistics – The Art and Science of Learning from Data. 4th Edition. Essex: Pearson Education Limited
- Caitlin C. Mothes, PhD and Katie Willi. 2023. Introduction to Data Analysis in. [Introduction to Data Analysis in R (rossyndicate.github.io)]
- Weisberg, S. 2005. Applied Linier Regression, 3𝑡ℎ Edition. New Jersey : John Wiley & Sons








