Penarikan Contoh Acak Berstrata (Stratified Random Sampling)


Di bidang penelitian dan statistik, memperoleh hasil yang akurat dan representatif adalah hal yang sangat penting. Data populasi umumnya besar dan mahal untuk didata secara menyeluruh, maka biasanya dilakukan penarikan sampel. Salah satu teknik penarikan sampel adalah stratified random sampling atau pengambilan sampel acak berstrata. Stratified random sampling adalah metode pengambilan sampel di mana populasi dibagi menjadi beberapa kelompok yang berbeda berdasarkan karakteristik tertentu.
Pada tulisan ini kita akan secara khusus mengupas teknik penarikan sampel menggunakan stratified random sampling. Mari kita telaah apa itu stratified random sampling, mengapa penting, dan bagaimana cara menerapkannya sampai dengan melakukan pendugaan nilai populasinya.
Mengapa Stratified Random Sampling?
Stratified random sampling adalah metode pengambilan sampel di mana populasi dibagi menjadi beberapa kelompok yang berbeda sebelum melakukan penarikan sampel. Setiap kelompok ini disebut dengan strata. Pembagian strata biasanya berdasarkan karakteristik tertentu yang memiliki keragaman yang besar/ heterogen antar stratanya namun cenderung homogen untuk setiap objek di dalam suatu strata. Dari setiap strata ini, sampel diambil secara acak. Tujuan utama dari stratified random sampling adalah memastikan setiap strata dari populasi terwakili dalam sampel akhir. Dengan demikian hasil penelitian lebih akurat dan dapat lebih menggambarkan kondisi seluruh populasi.
Berikut beberapa alasan penggunaan teknik stratified random sampling:
- Representasi yang Lebih Baik: Dengan memastikan bahwa setiap strata dalam populasi terwakili, stratified random sampling akan memberikan gambaran yang lebih akurat tentang populasi secara keseluruhan.
- Mengurangi Variabilitas: Dengan membagi populasi menjadi strata yang homogen, keragaman dalam masing-masing strata berkurang, di mana hal ini akan meningkatkan ketepatan pendugaan nilai populasi.
- Efisiensi: Metode ini bisa lebih efisien dibandingkan dengan penarikan sampel acak sederhana (simple random sampling), terutama ketika populasi memiliki variasi yang tinggi.
Tahapan dalam Stratified Random Sampling
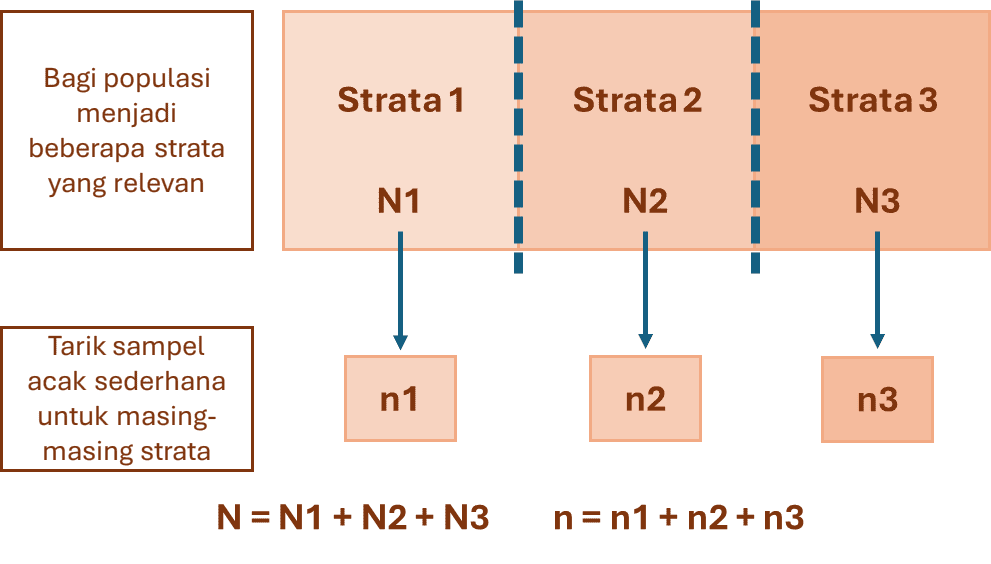

- Identifikasi Populasi: Tentukan populasi target yang ingin diteliti.
- Menentukan Strata: Bagi populasi menjadi strata berdasarkan karakteristik yang relevan (misalnya, usia, jenis kelamin, pendapatan, dll.).
- Menentukan Ukuran Sampel: Tentukan ukuran sampel total yang dibutuhkan dan bagaimana ukuran sampel ini akan dialokasikan di antara strata.
- Pengambilan Sampel Acak dalam Strata: lakukan pengambilan sampel acak dari setiap strata.
Alokasi Sampel di Setiap Strata
Banyaknya jumlah sampel untuk setiap strata dapat ditentukan dengan beberapa cara yaitu Alokasi Optimum, Alokasi Neyman dan Alokasi Proporsional.
Alokasi Optimum
Alokasi optimum berfokus pada pengurangan biaya atau peningkatan efisiensi pengambilan sampel dengan mempertimbangkan variabilitas dan biaya pengumpulan data di setiap strata. Tujuan dari alokasi optimum adalah mengalokasikan sumber daya secara lebih efisien dengan fokus lebih besar pada strata yang lebih bervariasi.
Misal pada populasi berukuran $N$ yang dibagi menjadi strata $N_1, N_2, \ldots ,N_H$ dan akan diambil sebanyak $n$ sampel. Misalkan varians pada strata ke-i adalah $\sigma_i^2$ dan biaya pada strata ke-i adalah $c_i$, maka jumlah sampel untuk strata ke-i ($n_i$) adalah:
$$n_i=n\times\frac{N_i\cdot \sigma_i/\sqrt{c_i}}{\sum_{h=1}^{H}N_h\cdot\sigma_h/\sqrt{c_k}} \qquad (1)$$
Alokasi Neyman
Alokasi Neyman dirancang untuk meminimalkan varians dari estimasi rata-rata populasi. Dengan menggunakan variabilitas dalam strata, metode ini memastikan bahwa strata dengan varians yang lebih besar mendapatkan lebih banyak sampel untuk meningkatkan keakuratan estimasi. Alokasi Neyman sangat efektif dalam penelitian yang bertujuan untuk menghasilkan estimasi yang sangat akurat dari rata-rata populasi.
Misal pada populasi berukuran $N$ yang dibagi menjadi strata $N_1, N_2, \ldots ,N_H$ dan akan diambil sebanyak $n$ sampel. Misalkan varians pada strata ke-i adalah $\sigma_i^2$ maka jumlah sampel untuk strata ke-i ($n_i$) adalah:
$$n_i=n\times\frac{N_i\cdot \sigma_i}{\sum_{h=1}^{H}N_h\cdot\sigma_k} \qquad (2)$$
Pada alokasi Neyman kita mengasumsikan bahwa biaya untuk satu unit sampel dari setiap strata adalah sama yaitu $c_1=c_2=\ldots=c_H$
Alokasi Proporsional
Ukuran sampel pada alokasi proporsional ditentukan berdasarkan proporsimya terhadap keseluruhan populasi. Tujuan utama dari alokasi ini adalah untuk memastikan bahwa setiap strata diwakili secara proporsional sesuai dengan ukurannya dalam populasi. Metode ini sederhana dan mudah diterapkan serta menghasilkan sampel yang representatif secara keseluruhan.
Misal pada populasi berukuran $N$ yang dibagi menjadi strata $N_1, N_2, \ldots ,N_H$ dan akan diambil sebanyak $n$ sampel. Jika menggunakan alokasi proporsional, maka jumlah sampel untuk strata ke-i ($n_i$) adalah:
$$n_i=n\times\frac{N_i}{\sum_{h=1}^{H}N_h}=n\times\frac{N_i}{N} \qquad (3)$$
Alokasi proporsional mengasumsikan bahwa biaya untuk satu unit sampel dari setiap strata adalah sama yaitu $c_1=c_2=\ldots=c_H$, dan ragam antar strata juga sama $\sigma_1^2=\sigma_2^2=\ldots=\sigma_H^2$.
Penduga Rataan Populasi
Pendugaan rata-rata populasi adalah proses analisis yang dilakukan mengestimasi nilai rataan untuk seluruh populasi berdasarkan informasi dari sampel yang dipilih secara acak pada setiap strata.
Rataan dan Varians per Strata
Misal $y_{hj}$ untuk $j=1,2, \ldots, n_h$ adalah data hasil sampel pada strata ke-h, maka nilai rata-rata untuk strata ke-h adalah:
$$\bar{y}_h=\frac{1}{n_h}\sum_{j=1}^{n_h}y_{hj} \qquad (4)$$
dan varians pada strata ke-h adalah:
$$s_h^2=\frac{1}{n_h-1}\sum_{j=1}^{n_h}(y_{hj}-\bar{y}_h)^2 \qquad (5)$$
Rataan dan Varians Populasi
Nilai dugaan untuk rataan populasi dapat diperoleh dengan menghitung rataan tertimbang dari nilai rataan masing-masing stratanya.
$$\bar{y}_{st}=\frac{1}{N}\sum_{h=1}^HN_h\bar{y}_h \qquad (6)$$
Adapun dugaan varians dari rataan tersebut adalah:
$$\hat{V}(\bar{y}_{st})=s_{\bar{y}_{st}}^2=\frac{1}{N^2}\sum_{h=1}^HN_h\cdot(N_h-n_h)\cdot \frac{s_h^2}{n_h} \qquad (7)$$
Berdasarkan Persamaan (6) dan (7) maka selang kepercayaan $(1-\alpha) 100$% bagi $\mu$ adalah:
$$\bar{y}_{st}\pm t_{\frac{\alpha}{2}}\cdot s_{\bar{y}_{st}} \qquad (8)$$
Penduga Total Populasi
Dalam beberapa penelitian, mungkin kita juga tertarik pada pendugaan total populasi dibandingkan rata-ratanya. Total nilai populasi ($\tau$) dapat diukur dengan cara yang serupa seperti Persamaan (6) tanpa membaginya dengan $N$.
$$\hat{\tau}_{st}=N\cdot \bar{y}_{st}=\sum_{h=1}^HN_h\bar{y}_h \qquad (9)$$
dengan varians yaitu:
$$\hat{V}(\hat{\tau}_{st})=s_{\hat{\tau}_{st}}^2=N^2s_{\bar{y}_{st}}^2=\sum_{h=1}^HN_h\cdot(N_h-n_h)\cdot \frac{s_h^2}{n_h} \qquad (10)$$
Berdasarkan Persamaan (9) dan (10) maka selang kepercayaan $(1-\alpha) 100$% bagi $\tau$ adalah:
$$\hat{\tau}_{st}\pm t_{\frac{\alpha}{2}}\cdot s_{\hat{\tau}_{st}} \qquad (11)$$
Ilustrasi
CONTOH SOAL
Untuk mengetahui kemampuan akademik siswa di suatu wilayah, dilakukan penarikan contoh acak sebanyak 60 siswa. Dengan indikasi adanya perbedaan kemampuan siswa antara sekolah dengan Akreditasi A, B dan C maka dilakukan penarikan contoh berstrata dengan hasil sebagai berikut:
Akreditasi A (25 dari 2.500 siswa):
87, 90, 82, 85, 88, 92, 79, 84, 86, 91, 83, 78, 86, 90, 87, 85, 89, 92, 84, 87, 91, 88, 85, 86, 83
Akreditasi B (15 siswa dari 1.500):
78, 82, 80, 79, 84, 81, 76, 85, 80, 83, 79, 77, 82, 81, 84
Akreditasi C (20 siswa dari 2.000):
70, 72, 75, 76, 71, 84, 78, 73, 76, 80, 72, 75, 87, 73, 70, 82, 76, 79, 74, 75
Berdasarkan data tersebut, hitunglah dugaan rata-rata nilai akademik siswa di wilayah tersebut dan selang kepercayaannya (95%).
Untuk menjawab pertanyaan ini maka kita dapat membaginya menjadi 3 langkah yaitu:
Menghitung Rata-rata dan Varians Setiap Strata
Nilai rata-rata dan varians per strata dapat dihitung menggunakan Persamaan (4) dan Persamaan (5). Berdasarkan persamaan tersebut maka diperoleh:
Rata-rata dan Varians per Strata
Akreditasi A:
> $\bar{y}_1=\frac{1}{25}\times(87+90+\ldots+83)=86,32$
> $s_1^2=\frac{1}{25-1}\times [(87-86,32)^2+(90-86,32)^2+\ldots+(83-86,32)^2]=13,73$
Akreditasi B:
> $\bar{y}_2=\frac{1}{15}\times(78+82+\ldots+84)=80,73$
> $s_2^2=\frac{1}{15-1}\times [(78-80,73)^2+(82-80,73)^2+\ldots+(84-80,73)^2]=7,07$
Akreditasi C:
> $\bar{y}_3=\frac{1}{20}\times(70+72+\ldots+75)=75,90$
> $s_3^2=\frac{1}{20-1}\times [(70-75,90)^2+(72–75,90)^2+\ldots+(75-75,90)^2]=21,25$
Menghitung Dugaan Rata-rata Populasi
Nilai dugaan rata-rata populasi dapat kita hitung menggunakan Persamaan (6) dengan hasil sebagai berikut:
Dugaan Rata-rata Seluruh Populasi
$\begin{aligned}\bar{y}_{st} &= \frac{1}{N}\sum_{h=1}^H N_h\bar{y}_h \\\\ &= \frac{1}{6000}\times (2500\cdot86,32+1500\cdot80,73+2000\cdot75,90) \\\\ &= 81,45\end{aligned}$
Sampai di sini, kita sudah mendapatkan nilai dugaan rata-rata untuk populasi yaitu sebesar 81,45. Angka ini berarti, secara rata-rata, nilai akademik siswa di wilayah tersebut adalah sebesar 81,45.
Menghitung Selang Kepercayaan Rata-rata
Pada langkah ini, kita perlu menghitung nilai varians dan standar deviasi dari dugaan rata-rata terlebih dahulu menggunakan Persamaan (7).
Varians dan standar deviasi dugaan rata-rata populasi
$\begin{aligned}s_{\bar{y}_{st}}^2 &= \frac{1}{N^2}\sum_{h=1}^HN_h\cdot(N_h-n_h)\cdot \frac{s_h^2}{n_h} \\\\ &= \frac{1}{6000^2}\times \left(2500\cdot(2500-25)\cdot\frac{13,73}{25} + 1500\cdot(1500-15)\cdot\frac{7,07}{15} + 2000\cdot(2000-20)\cdot\frac{21,25}{20}\right) \\\\ &= 0,2404\end{aligned}$
$\begin{aligned} s_{\bar{y}_{st}}=\sqrt{s_{\bar{y}_{st}}^2}=0,4903\end{aligned}$
Berikutnya, kita gunakan nilai $t_{(0.025, db)}$. Untuk menghitung derajat bebas, kita dapat menggunakan $\sum_{h=1}^H (n_h-1)$, dan pada soal ini berarti $24+14+19=57$. Melalui berbagai software (Misal Ms. Excel) kita memperoleh nilai $t_{(0.025, 57)}=2,002465$.
Dengan demikian, maka selang kepercayaan 95% bagi rata-rata adalah:
Selang kepercayaan 95% untuk rata-rata
$\begin{aligned}bb & =\bar{y}_{st}-t_{(0,025, db=57)}\cdot s_{\bar{y}_{st}}\\\\&=81,45-2,002465\cdot 0,4903\\\\&=80,47\end{aligned}$
$\begin{aligned}ba & =\bar{y}_{st}+t_{(0,025, db=57)}\cdot s_{\bar{y}_{st}}\\\\&=81,45+2,002465\cdot 0,4903\\\\&=82,43\end{aligned}$
Berdasarkan hasil di atas, maka kita peroleh bahwa dengan tingkat kepercayaan 95%, kita meyakini rata-rata nilai akedemik di wilayah tersebut berkisar antara 80,47 sampai dengan 82,43.
Referensi
- Lohr, S L. (2010), Sampling: Design and Analysis 2nd Editon, Brooks/Cole Cengage Learning, Boston, USA
- Scheaffer, R L., & Mendenhall, W., Ott, L. R., Gerow, K. (2012). Elementary Survey Sampling 7th Edition, Brooks/Cole Cengage Learning, Boston, USA








