Pengujian Proporsi dan Nilai Tengah Satu Populasi

Tujuan utama dari penelitian adalah untuk menunjukkan apakah data yang ada dapat mendukung suatu pernyataan atau prediksi. Yang dimaksud dengan pernyataan di sini adalah hipotesis tentang populasi. Sebagai contoh, ketika lembaga survei melakukan hitung cepat hasil pemilihan kepala daerah dengan mengambil sampel dari beberapa TPS, maka harapannya adalah dari data tersebut dapat memperkirakan atau menduga hasil sesungguhnya dan menarik kesimpulan tertentu. Contoh lain misalkan, suatu perusahaan mengklaim bahwa waktu yang mereka perlukan untuk menyelesaikan setiap keluhan pelanggan adalah tidak lebih dari 30 menit. Untuk menguji klaim tersebut, dapat melalui pengambilan beberapa contoh secara acak kemudian melakukan uji signifikansi dengan hipotesis tertentu.

Setiap uji signifikansi mengharuskan beberapa asumsi atau kondisi tertentu yang dipenuhi. Beberapa asumsi yang biasa menjadi perhatian adalah prinsip acak dalam pengambilan data sampel, banyaknya jumlah sampel bentuk dari sebaran populasi.

Setiap uji signifikansi memiliki dua hipotesis tentang parameter populasi. Yang pertama adalah Hipotesis Nol/Null Hypothesis ($H_0$) dan Hipotesis Alternatif ($H_a$ atau $H_1$). $H_0$ adalah pernyataan tentang parameter yang mengandung nilai tertentu atau klaim tentang populasi yang terlebih dahulu diasumsikan benar. Sementara $H_1$ berisi pernyataan tandingan yang berlawanan dengan $H_0$. Berdasarkan hipotesis ini nantinya kita akan menolak $H_0$ jika data yang ada mendukung $H_1$, sementara itu kita tidak menolak $H_0$ saat data tidak mundukung penolakan $H_0$.

Hipotesis yang diuji dapat bersifat satu arah maupun dua arah. Contoh hipotesis satu arah adalah seperti ilustrasi klaim perusahaan yang menyatakan bahwa waktu yang diperlukan untuk menyelesaikan setiap keluhan tidak lebih dari 30 menit.

Dalam menulis hipotesis satu arah sering kali pada $H_0$-nya hanya menggunakan tanda $=$ sehingga hipotesis di atas sama saja dengan

Yang menjadi ciri dari hipotesis 1 arah adalah pada $H_1$ menggunakan tanda $>$ atau $<$ tergantuk konteks masalahnya. Sementara itu untuk hipotesis dua arah pada $H_1$ menggunkaan tanda $\neq$. Sebagai contoh:

Dalam uji signifikansi biasanya tujuan yang diharapkan adalah membuktikan bahwa $H_0$ salah. Pada saat kita menolak $H_0$ hasil pengujian akan bersifat konklusif, yang bermakna pada tingkat keyakinan tertentu, pernyataan $H_0$ adalah salah dan yang benar adalah pernyataan $H_1$. Namun sebaliknya ketika tidak menolak $H_0$, hasil pengujian bersifat inkonklusif dan tidak berarti $H_0$ benar. Hal ini hanya menunjukkan tidak cukup bukti bagi kita untuk menolak $H_0$.

Statistik uji menunjukkan seberapa jauh jarak estimasi titik berdasarkan data contoh terhadap nilai parameter yang menjadi hipotesis pada $H_0$. Pengukuran jarak ini biasanya berdasarkan berapa kali nilai galat baku/standard error antara besaran estimasi titik dan nilai parameternya. Sebagai contoh klaim perusahaan sebelumnya, misalkan berdasarkan perhitungan dari 20 contoh acak didapat rata-rata waktu penyelesaian keluhan pelanggan adalah 35 menit dengan simpangan baku 5 menit. Dari informasi ini nanti akan diperoleh besaran statistik ujinya.

Untuk menginterpretasikan statistik uji, biasa menggunakan p-value. P-value menunjukkan besarnya peluang dari statisttik uji kita mendukung $H_0$. Jika nilai statistik uji jatuh pada area ekor sebaran (tergantung tingkat kepercayaan yang diharapkan), maka kita akan menolak $H_0$. Kesimpulan ini berawal dengan mengasumsikan bahwa $H_0$ benar, berdasarkan sebaran percontohan, jika $H_0$ benar maka kemungkinan statistik uji tersebut jatuh jauh pada ekor-ekor sebaran adalah sesuatu yang tidak lazim. Artinya, semakin kecil p-value semakin tidak lazim pernyataan $H_0$ bernilai benar.

Sebagai ilustrasi perhatikan gambar berikut ini:

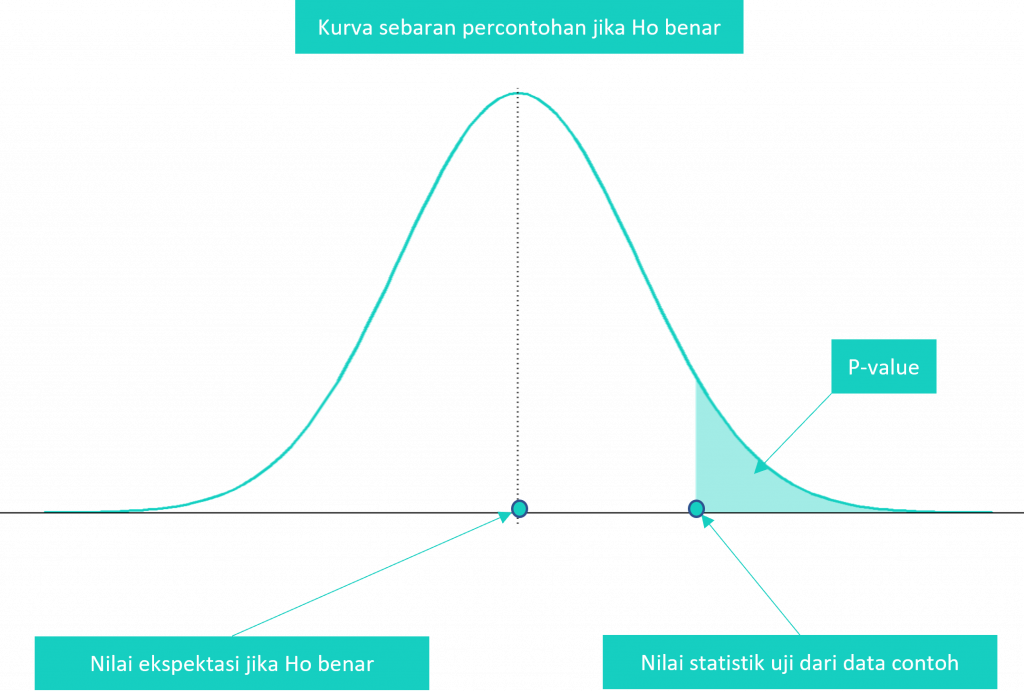
Dengan menganggap $H_0$ benar, maka nilai harapan dari statistik uji seharusnya akan jatuh di sekitar nilai tengahnya. Jika statistik uji yang ada hasil data contoh berada jauh dari nilai harapannya tentu hal tersebut merupakan sesuatu yang tidak lazim. Semakin jauh nilai statistik uji dari nilai harapan maka semakin kecil p-value-nya, sehingga pada tingkat kepercayaan tertentu kita dapat menyimpulkan bahwa pernyataan pada $H_0$ kemungkinan tidak benar. Di sini kita selalu menyatakan pada tingkat kepercayaan tertentu, karena walaupun peluangnya kecil bukanlah suatu yang mustahil bahwa data yang kita ambil kebetulan sebagian besar jauh dari nilai tengahnya. Kesalahan inilah yang disebut sebagai kesalahan tipe I.

Langkah terakhir dalam proses uji signifikansi adalah penarikan kesimpulan, apakah akan menolak $H_0$ atau sebaliknya. Saat kita menolak $H_0$ maka pada tingkat keyakinan tertentu kita yakin bahwa $H_0$ salah. Namun, yang perlu diingat seperti telah disampaikan sebelumnya, saat statistik uji menunjukkan tidak tolak $H_0$ maka kesimpulannya bersifat inkonklusif serta tidak berarti menunjukkan bahwa $H_0$ benar. Dari data contoh yang ada belum cukup bukti untuk menyatakan bahwa $H_0$ salah.

Dalam penarikan kesimpulan kita menetapkan batas dari kesalahan jenis I yaitu sebesar $\alpha$. Nilai $\alpha$ yang umum dipakai adalah 5%, 1% atau 10%. Meskipun tidak ada aturan besaran $\alpha$ yang harus dipilih, nilai 5% adalah yang paling umum digunakan. Namun pada bidang-bidang yang memerlukan presisi lebih tinggi tentu dapat menetapkan nilai $\alpha$ yang lebih kecil, begitu pula sebaliknya.

Untuk variabel yang bersifat kategorik, yang menjadi perhatian kita adalah adalah besarnya proporsi kategori tertentu dari suatu populasi. Adapun statistik uji yang digunakan adalah uji z.

Terkadang untuk mengambil keputusan, alih-alih menghitung p-value dari statistik uji, kita menghitung z-score seagai titik kritis dari $\alpha$. Dalam hal ini pengambilan keputusan berkebalikan dari sebelumnya,

untuk pengujian 2 arah, tolak $H_0$ jika $|z_{hit}| > |z_{\alpha/2}|$,

untuk pengujian 1 arah dan wilayah penolakan di sisi kanan, tolak $H_0$ jika $z_{hit} > z_{\alpha}$

dan untuk pengujian 1 arah dimana wilayah penolakan berada di sisi kiri, tolak $H_0$ jika $z_{hit} < z_{\alpha}$.

Sebagai contoh untuk $z_{\alpha/2 = 0,025} = 1,96$, $z_{\alpha = 0,05} = 1,645$, dan $z_{\alpha = 0,1} = 1,28$.

Berikut beberapa ilustrasi yang dapat kita selesaikan menggunakan uji signifikansi proporsi.

Setelah pelaksanaan pemilihan kepala daerah di kota X yang diikuti oleh 2 calon, lembaga survei ABC melakukan hitung cepat dengan menarik sampel secara acak dari berbagai TPS sebanyak 1500 sampel. Dari sampel tersebut diketahui bahwa calon A memperoleh suara 790 suara, sementara calon B memperoleh sisanya (710 suara). Berdasarkan hasil ini, calon A menyatakan bahwa dirinya akan memenangkan pemilihan. Dengan melakukan uji signifikasi proporsi apakah klaim calon A tersebut dapat diterima?

Untuk menjawab pertanyaan ini kita perlu menjalankah langkah-langkah yang sudah dijelaskan sebelumnya.

# Ms. Excel
# Karena area penolakan di sisi kanan maka p-value = 1 - p(Z < z)
=1 - NORM.S.DIST(2.0698;TRUE) 

# Output : 0.019235539

# R : menghitung dari ekor kanan
pnorm(2.0698, lower.tail = F)
# Output : 0.01923554

# Python
from scipy.stats import norm
1 - norm.cdf(2.0698)

# output : 0.01923553869323502

Suatu perusahaan menyatakan bahwa 70% pelanggannya puas terhadap produk mereka. Anggaplah kita tidak tertarik untuk melihat apakah nilai sebenarnya lebih tinggi atau lebih rendah dari angka tersebut. Kita hanya tertarik untuk melihat apakah nilai 70% tersebut dapat diterima. Untuk itu kita melakukan survei dengan mengambil sampel acak dari pelanggan produk perusahaan tersebut. Dari sana diperoleh hasil 136 dari 200 responden menyatakan puas. Ujilah pernyataan perusahaan berdasarkan data tersebut!

=NORM.S.DIST(-0.6172; TRUE)

#output : 0,268551

Untuk data kuantitatif, uji signifikansi pada umumnya mengacu pada nilai tengah populasi ($\mu$). Contohnya, kepala sekolah pada sekolah A mengatakan bahwa siswa sekolah tersebut memiliki kemampuan bahasa inggris yang baik dengan rata-rata skor TOEFL ITP setidaknya 530. Untuk menunjukkan hal ini dapat menggunakan uji signifikansi nilai tengah.

Dalam pengujian signifikansi nilai tengah, terdapat beberapa hal yang harus menjadi perhatian yaitu apakah ragam populasinya diketahui dan apakah jumlah contoh yang diambil cukup besar (berdasarkan banyak ahli statistika sampel lebih dari 30 dikatakan besar). Karena kedua hal tersebut akan menentukan statistik uji yang digunakan.

Dalam prakteknya sangat jarang nilai ragam populasi diketahui, sehingga untuk kondisi ini jika ragam tidak diketahui dan jumlah sampel kecil ($n < 30$) maka pengujian menggunakan statistik uji $t$ dengan derajat bebas (db) = $n-1$.

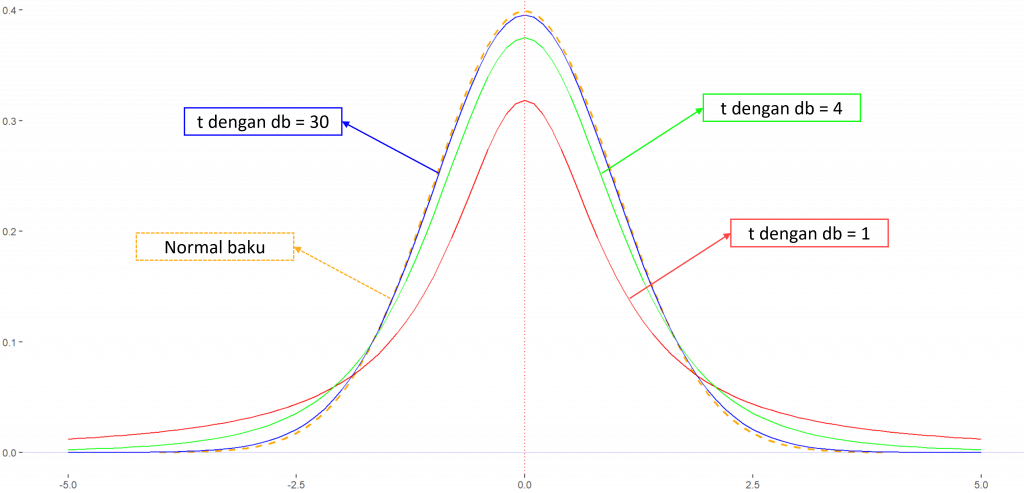
Jika ragam tidak diketahui dan jumlah sampel besar ($n \geq 30$), untuk kondisi ini pada prinsipnya statistik uji yang digunakan tetap $t$ karena ragam populasi tidak diketahui. Pada software statistik, pengujian juga dilakukan dengan statistik uji $t$. Namun untuk nilai $t$ dengan derajat bebas yang semakin besar (jumlah sampel besar) maka nilainya $t$ akan semakin mendekati nilai $z$, sehingga pendekatan sebaran normal dapat digunakan.

Kepala sekolah pada sekolah A mengatakan bahwa siswa sekolah tersebut memiliki kemampuan bahasa inggris yang baik dengan dan secara rata-rata memiliki skor TOEFL ITP 530. Selanjutnya dilakukan penarikan sampel secara acak sebanyak 10 siswa dan diperoleh nilai TOEFL ITP dari 10 siswa tersebut adalah 536, 498, 480, 516, 554, 542, 528, 475, 496 dan 544. Misalkan berdasarkan informasi terdahulu diketahui distribusi nilai TOEFL menyebar Normal dengan ragam $20^2$, ujilah pernyataan kepala sekolah tersebut pada tingkat kepercayaan 95%.

Hipotesis ujinya adalah

$H_0 : \mu = 530\;vs\;H_1 : \mu \neq 530$

Pada ilustrasi ini jumlah sampel $n = 10$ dan nilai $\sigma^2$ diketahui yaitu $20^2$, atau $\sigma=20$. Sehingga untuk menyelesaikan soal ini kita menggunakan statistik uji $z$.

Nilai statistik uji:

$$\begin{aligned}\bar{x} &= \frac{\sum_{i=1}^{10} x_i}{10} = \frac{536 + 498 + … + 544}{10} = 516,9\\\\z_{hit} &= \frac{516,9-530}{20/\sqrt{10}} = -2,0713\end{aligned}$$

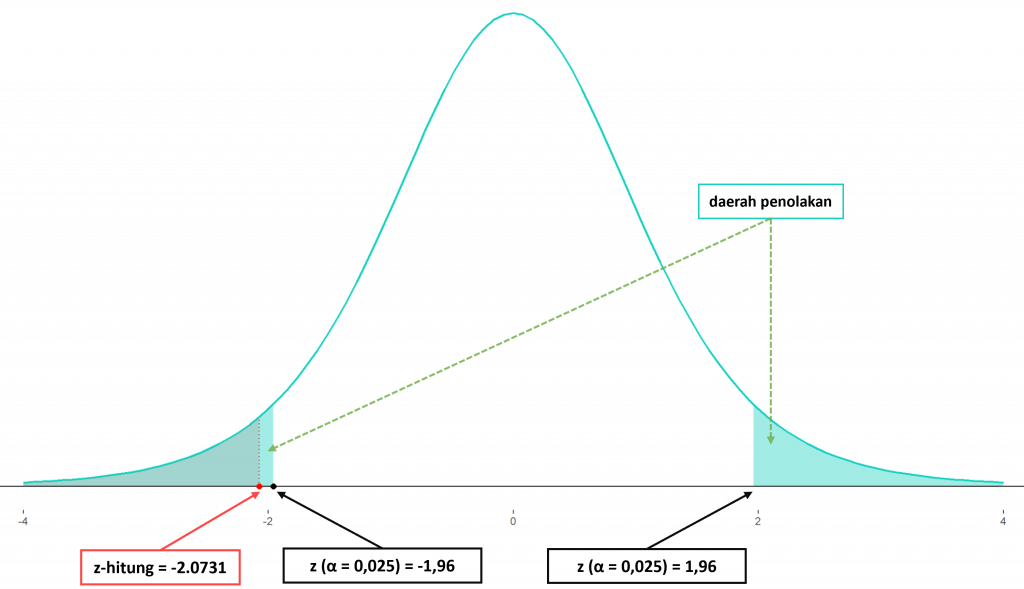
Menggunakan Ms Excel, nilai p-value dari statistik uji tersebut adalah $0,019$. Nilai ini lebih kecil dari $\alpha/2=0,025$, yang berarti tolak $H_0$. Atau jika menggunakan nilai statistik ujinya hasilnya adalah $|-2,0731| > 1,96$, sehingga keputusannya adalah tolak $H_0$. Kesimpulan yang dapat diambil adalah pada tingkat kepercayaan $95\%$, maka rata-rata Nilai TOEFL ITP dari sekolah tersebut tidak sama dengan 530. Walaupun uji yang dilakukan adalah dua arah namun melihat diri nilainya sepertinya rata-rata yang sesungguhnya berada di bawah 530.

Hasil dari kajian teoritis menunjukkan mesin produksi baru mampu menyelesaikan seluruh proses pembuatan produk kurang dari 45 menit. Untuk meyakinkan hasil tersebut, perusahaan melakukan pengujian secara acak terhadap 8 mesin baru. Hasil yang diperoleh (dalam menit) adalah 43, 41, 46, 44, 44, 47, 42, 46. Jika lamanya waktu mesin untuk memproses produk menyebar normal maka pada tingkat kepercayaan 95% apakah pengujian tersebut mampu menunjukkan bahwa mesin baru tersebut secara rata-rata memeroses lebih cepat dari 45 menit?

Untuk mendukung pernyataan tersebut kita menginginkan hipotesis alternatifnya adalah rata-rata waktu produksi mesin baru lebih cepat dari 45 menit.

Hipotesis ujinya adalah

$$H_0 : \mu \geq 45\;vs\;H_1 : \mu < 45$$

Dalam contoh ini jumlah sampel sedikit ($n=8$) dan ragam populasi tidak diketahui, maka statistik uji yang akan digunakan adalah $t$ dengan derajat bebas ($db = 8-1 = 7$).

$$\begin{aligned}\bar{x} &= \frac{\sum_{i=1}^{8} x_i}{8} = \frac{43 + 41 + … + 46}{8} = 44,125\\\\s &= \sqrt{\frac{\sum_{i=1}^{8} (x_i-\bar{x})^2}{8-1}} \\\\&= \sqrt{\frac{(43-44,125)^2 + … + (46-44,125)^2}{7}}\\\\&=2,1\\\\t_{hit} &= \frac{44,125-45}{2,1/\sqrt{8}} = -1,1784\end{aligned}$$

# Nilai t-hitung (db = 7) 
=T.DIST(C15;7;TRUE)

# output : 0.1386

# Nilai t alpha=0.05 db = 7
=T.INV(0.05;7)

# output : -1.8946

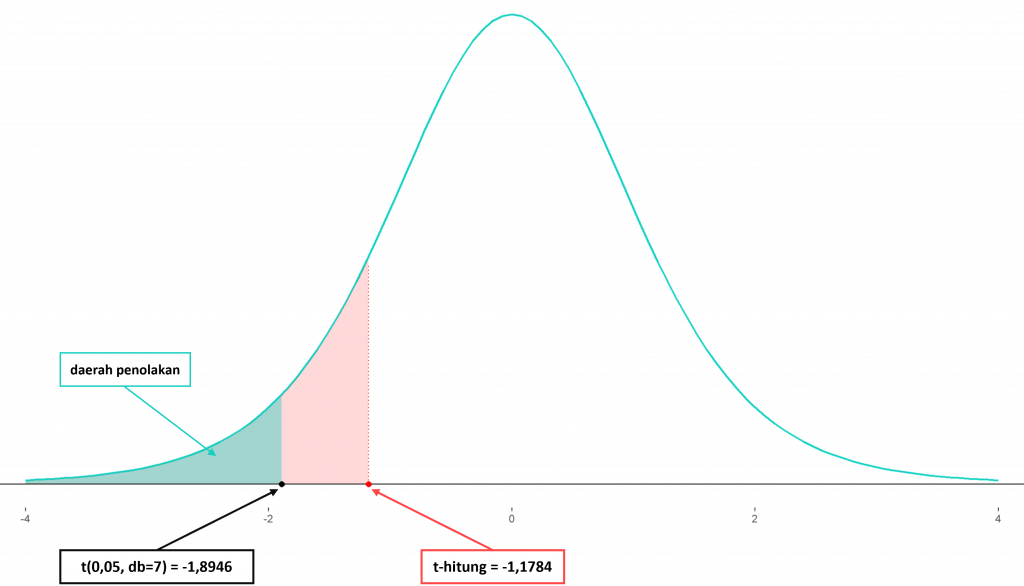
Karena $H_1$ bertanda “$<$” maka daerah penolakan berada di sisi kiri. Dengan menggunakan Ms Excel, kita peroleh p-value $= 0,1386$ artinya p-value $> \alpha$. Ataupun dengan membandingkan nilai $t_{hit} = -1,1784$ terhadap $t_{(\alpha, db=7)} = -1,8946$ maka $t_{hit} > t_{(\alpha, db=7)}$ (masih berada di dalam area penerimaan $H_0$). Keputusannya adalah tidak tolak $H_0$ (inkonklusif), dan kesimpulan yang dapat diambil yaitu belum cukup bukti untuk menyatakan bahwa kecepatan mesin baru untuk menyelesaikan seluruh proses pembuatan produk kurang dari 45 menit.

Berdasarkan sebuah studi fiktif yang melibatkan 100 sampel acak pekerja di suatu daerah, rata-rata penghasilannya adalah Rp 4.500.000 dengan simpangan baku sebesar Rp 750.000. Pada tingkat kepercayaan 99% apakah pernyataan secara rata-rata penghasilan pekerja di daerah tersebut lebih dari Rp. 4.250.000 secara statistik dapat dibenarkan.

Ilustrasi ini merupakan contoh kondisi ragam populasi tidak diketahui dan jumlah sampel besar. Untuk itu kita bisa menggunakan statistik uji z.

$H_0 : \mu \leq 4.250.000\;vs\;H_1 : \mu > 4.250.000$

Statistik uji :

$\begin{aligned}z_{hit} &= \frac{4.500.000-4.250.000}{750.000/\sqrt{100}} = 3,3333\end{aligned}$

Nilai p-value untuk $z_{hit}=3,3333$ adalah $0.000429$. Berdasarkan nilai p-value yang jauh lebih kecil dari $\alpha = 0.01$ maka keputusannya adalah tolak $H_0$ dan kesimpulannya adalah pada tingkat keyakinan 99% rata-rata penghasilan dari pekerja pada daerah tersebut lebih dari Rp 4.250.000.

Agresti, A., Franklin, C., Klingenberg, B. (2017), Statistics The Art and Science of Learning from Data 4th Editon, Pearson Education.

• Sebaran Peubah Acak Diskret
• Ukuran Penyebaran Data (Data Dispersion)
• Ukuran Pemusatan Data (Central Tendency)