Membangkitkan Data Simulasi Model Regresi dengan Numpy

Pada tutorial ini, kita akan mempelajari cara membangkitkan data simulasi menggunakan Python yaitu dengan pustaka numpy. Data yang dibangkitkan merupakan data numerik dan nantinya dapat digunakan untuk melakukan simulasi pada model regresi linier.

Skenario data simulasi yang akan dibangkitkan adalah sebagai berikut:

• Jumlah data yang dibangkitkan sebanyak 10.000
• Terdapat 10 Peubah bebas dengan nama $X_1, X_2, …, X_{10}$
• Peubah $X_1$ sampai dengan $X_{5} \sim Normal(\mu=10, \; \sigma^2=9)$
• Peubah $X_{6}$ dan $X_{7} \sim MN(\mu=[50, 20], \; \sum=[[25, 12], [12, 16]])$
• Peubah $X_8$ menyebar normal dan memiliki korelasi terhadap $X_1$ sebesar ($\rho=-0.80$)
• Peubah $X_9 = -5X_1 + \mu_1$ dimana $\mu \sim Normal(\mu=0,\; \sigma^2=5)$
• Peubah $X_{10} = 3X_6 + \mu_2$ dimana $\mu \sim Normal(\mu=10,\; \sigma^2=5)$
• Peubah $Y$ diperoleh melalui kombinasi linear $Y=\beta_0 + \beta_1X_1 + \beta_2X2 + … + \beta_{10}X_{10} + \epsilon$ misal $\epsilon \sim Normal(\mu=100, \; \sigma^2=625)$
• $\beta_0 = 15$; $\; \beta_1 = \beta_2 = … = \beta_{5} = 10$; $\; \beta_6 = \beta_7 = 5$; $\; \beta_{8} = \beta_{9} = \beta_{10} = 0.1$

Secara umum berdasarkan daftar di atas semua data yang dibangkitkan akan mengikuti sebaran Normal dengan beberapa variasi nilai tengah dan varians. Selain itu pada beberapa variabel akan diberikan konstrain tertentu, sehingga memiliki hubungan kuat dengan variabel lainnya atau terdapat multikolinearitas. Hal ini biasanya harus ditangani ketika kita melakukan pemodelan regresi linear khususnya jika digunakan sebagai basis inferensi.

Lihat : Membangkitkan Bilangan Acak untuk Sebaran Tertentu dengan Python Numpy

Untuk pembangkitan bilangan acak kita akan menggunakan pustaka numpy, namun sebagai alat bantu visualisasi dan manajemen data beberapa pustaka lain juga akan digunakan.

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

Fungsi normal pada numpy memiliki 2 parameter utama yaitu loc dan scale. Parameter loc menunjukkan nilai tengah dari distribusi yang akan dibangkitkan, sementara scale menunjukkan standar deviasi (akar kaudrat dari varians).

Sintaks untuk membangkitkan data variabel X adalah sebagai berikut:

# Membuat list variabel X
col_X = ["X" + str(i) for i in range(0, 11)]

n = 10_000

X = pd.DataFrame(index=np.arange(n), columns=col_X)


# randomstate/seed
rs = np.random.RandomState(100)


# menyiapkan data untuk intersep (1)
X["X0"] = [1] * n


# Membangkitkan 10.000 data untuk setiap var X1 hingga X5
# menyebar Normal (10, 9)
for i in range(1, 6):
    X[col_X[i]] = rs.normal(loc=10, scale=np.sqrt(9), size=n)


# X6 dan X7
# Membangkitkan 10.000 data X6 dan X7 Multivariate Normal
# mean X6 = 50, mean X7 = 20
# varians X6 = 25 dan X7 = 16
# cov(X6, X7) = 12
mean = [50, 20]
cov = np.array([[25, 12], [12, 16]])
X[['X6', 'X7']] = rs.multivariate_normal(mean, cov, size=n)


# X8
# Transformasi X8 dengan korelasi (-0.8) thd X1
rho_1_8 = -0.8
X['X8'] = rs.normal(loc=0, scale=1, size=n)
X['X8'] = rho_1_8 * X['X1'] + np.sqrt(1 - rho_1_8**2) * X['X8']


# X9
mu_9 = rs.normal(loc=0, scale=np.sqrt(5), size=n)
X['X9'] = -5 * X['X1'] + mu_9


# X10
mu_10 = rs.normal(loc=10, scale=np.sqrt(5), size=n)
X['X10'] = 3 * X['X6'] + mu_10

Penjelasan ringkas sintaks tersebut adalah:

• Membuat dataframe yang akan menyimpan data untuk setiap variabel X
• Menggunakan RandomState 100 (bebas menggunakan angka berapapun, namun jika ingin memperoleh angka acak yang sama persis dengan tutorial ini dapat menggunakan nilai 100)
• Untuk $X_1$ sampai $X_5$ kita bangkitkan 10.000 bilangan acak yang menyebar $Normal(\mu=10, \; \sigma^2=9)$
• Untuk $X6$ dan $X_7$ kita bangkitkan 10.000 pasangan bilangan acak yang menyebar multivariat normal seperti spesifikasi di atas menggunakan fungsi multivariate_normal dengan matriks varians-kovarian sebagai berikut: $$\begin{bmatrix}25 & 12 \\ 12 & 16\end{bmatrix}$$

• $X_8$, pertama kita bangkitkan bilangan acak yang menyebar sama dengan $X_1$ selanjutnya dengan melakukan transformasi menggunakan formula $ \rho X_1 + \sqrt{(1-\rho^2)}X_8$ maka variabel $X_8$ yang baru akan memiliki korelasi terhadap $X_1$ sebesar $-0.8$.
• Untuk $X_9$ merupakan kombinasi linear antara $X_1$ ditambah dengan suatu bilangan acak yang menyebar $Normal(\mu=0, \; \sigma^2=5)$
• Untuk $X_10$ merupakan kombinasi linear antara $X_6$ ditambah dengan suatu bilangan acak yang menyebar $Normal(\mu=10, \; \sigma^2=5)$

Setelah membangkitkan data-data tersebut kita dapat melihat karakteristik yang ada, sekaligus untuk menguji apakah sudah sesuai dengan yang diharapkan.

Pada objek dataframe pandas terdapat method describe untuk menampilkan statistik 5 serangkai. Dalam kode berikut kita kombinasikan dengan fungsi np.round untuk membulatkan 2 angka desimal agar lebih mudah dibaca.

Python

np.round(X.describe(), decimals=2)

Output

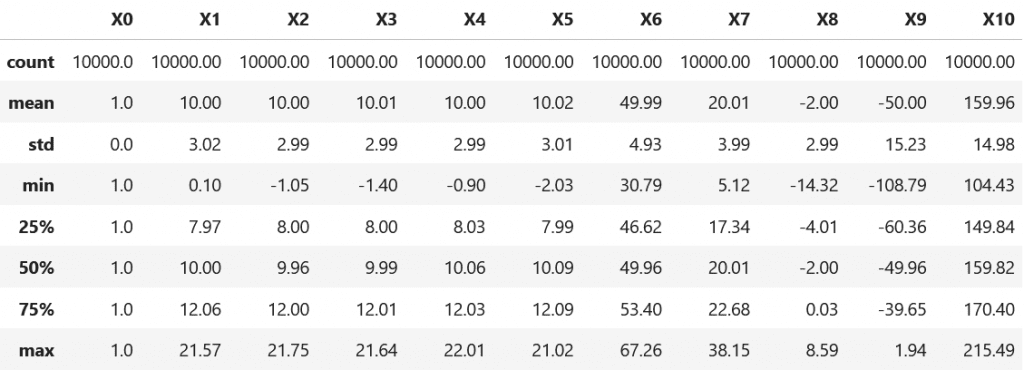
Dari tabel di atas dapat dilihat bahwa data hasil pembangkitan untuk $X_1$ hingga $X_5$ memiliki rata-rata sekitar 10 serta standar deviasi sekitar 3 (varians = 9) dimana artinya data mengikuti sebaran yang diharapkan.

Begitu pula untuk $X_6$ dan $X_7$ dimana masing-masing memiliki rata-rata untuk $X_6$ sekitar 50 (49,99) dan $X_7$ sekitar 20 (20,01). Untuk standar deviasi $X_6$ adalah sekitar 5 (4,93) dan $X_7$ sekitar 4 (3.99).

Adapun untuk $X_8, X_9, X_10$ yang merupakan kombinasi linear dari variabel lain kita dapat mengeceknya dengan menghitung ekspected value dari sebaran masing-masing peubah. Jika dilakukan perhitungan maka hasil yang diperoleh juga sudah sesuai kriteria yang diharapkan.

Selain nilai di atas, dapat pula dilihat dari bentuk kurva sebaran pada masing-masing variabel yang sudah terlihat mengikuti sebaran normal. Untuk menampilkannya dapat menggunakan sintaks berikut ini:

Python

fig, axes = plt.subplots(3, 4, figsize=(20, 8), sharex=False)

for idx, col in enumerate(X.columns):
    g = sns.histplot(data=X[col], bins=30, color="#16cfc1",
                     stat="density", ax=axes[idx // 4, idx % 4])
    g.set(ylabel=None, xlabel=None)
    g.axes.set_title(col, fontsize=16)
    
fig.tight_layout()
plt.show()

Output

Pada beberapa variabel yang dibangkitkan akan memiliki korelasi tertentu yang cukup tinggi. Beberapa yang pasti memiliki korelasi tinggi yaitu $X_1$ adn $X_8$, dimana secara eksplisit kita tentukan korelasi sebesar $-0,8$. Variabel $X_6$ dan $X_7$ juga akan memiliki korelasi tinggi jika melihat nbesaran ilai kovarian yang ditetapkan antara kedua variabel. Selanjutnya $X_9$ dan $X_1$ dimana $X_9$ merupakan kombinasi linier dari $X_1$ dan suatu bilangan acak lainnya. Hal yang sama juga berlaku untuk $X_10$ dan $X_6$.

Untuk memastikan data yang dibangkitkan memenuhi kriteria tersebut dapat dilihat melalui matriks korelasi seperti berikut ini.

Python

corr = X.corr()

# Menampilkan korelasi dalam bentuk Heatmap
f, ax = plt.subplots(figsize=(8, 6))
mask = np.triu(np.ones_like(corr, dtype=bool))
cmap = sns.diverging_palette(230, 20, as_cmap=True)
sns.heatmap(corr, mask=mask, cmap=cmap)

# Matriks Korelasi dari X1 - X10 (tanpa X0)
np.round(corr.iloc[1: ,1:], decimals=2)

Output

Dari heatmap dapat terlihat bahwa $X_1$ memiliki korelasi yang kuat dengan $X_8$ dan $X_9$ yang artinya sesuai dengan kriteria. Adapun nilainya adalah -0,8 untuk $X_1$ dan $X_8$ serta -0,99 untuk $X_1$ dan $X_9$. Korelasi antara $X_6$ dan $X_7$ juga cukup tinggi yaitu 0,6 hal ini sesuai jika melihat nilai kovarian antara kedua variabel. Begitu pula dengan korelasi antara $X_6$ dan $X_{10}$ sangat tinggi dikarenakan salah satunya merupakan kombinasi dari variabel lainnya.

Melihat dari hasil tersebut kita dapat meyakini bahwa data simulasi yang dibangkitkan sudah sesuai. Selanjutnya kita tinggal membangkitkan data acak untuk variabel Y. Variabel ini sendiri kita bangun berdasarkan kombinasi linear dari setiap variabel X ditambah dengan suatu nilai acak lainnya (dalam contoh ini disebut $\epsilon$).

Python

beta = [15, 10, 10, 10, 10, 10, 5, 5, 0.1, 0.1, 0.1]

# Membangkitkan variabel Y
rand = rs.normal(100, np.sqrt(625), n)
Y = np.matmul(X, beta) + rand


# Menyimpan X dan Y pada variabel data_sim
# drop X0
data_sim.drop("X0", axis=1, inplace=True)
data_sim["Y"] = Y

print(data_sim.head())


# Menyimpan Data dalam format CSV
data_sim.to_csv('data_sim.csv', index=False)

Output

Variabel Y dibangkitkan berdsarkan kombinasi linear semua variabel X dikalikan dengan koefisien beta tertentu. Namun agar persamaan X dan Y tidak menjadi sempurna, maka kita juga tambahkan bilangan cak lainnya, dalam contoh ini menyebar normal.

Setelah kita dapatkan seluruh variabel termasuk Y, kita dapat menyimpan data simulasi tersebut misalkan pada variabel baru. Adapun dalam contoh ini variabel $X_0$ tidak ikut disimpan. Hal ini dikarenakan penggunaannya dari awal hanya agar memudahkan kita dalam menghitung perkalian koefisien $\beta$ dan matriks $X$. Namun tidak ada permasalahan jika ingin ikut disimpan. Data simulasi tersebut juga dapat disimpan ke dalam format csv untuk digunakan pada kesempatan lain.

Data simulasi yang sudah dibuat dapat kita gunakan pada berbagai proyek yang berkaitan dengan Regresi. Kita dapat menggunakan pustaka seperti statsmodel untuk melakukan inferensi atau scikitlearn atau lainnya untuk bersimulasi dengan berbagai teknik machine learning khususnya model regresi.

Berikut adalah ilustrasi ringkas bagaimana penggunaan data tersebut khususnya dengan menggunakan statsmodel. Kita akan melihat bagaimana kebaikan model melalui nilai $R^2$ serta melihat variabel mana saja yang signifikan.

Python

import statsmodels.api as sm

data = pd.read_csv('data_sim.csv')

exog = sm.add_constant(data.iloc[:,:-1], prepend=False)
endog = data["Y"]

ols = sm.OLS(endog=endog, exog=exog).fit()

print(ols.summary())

Output

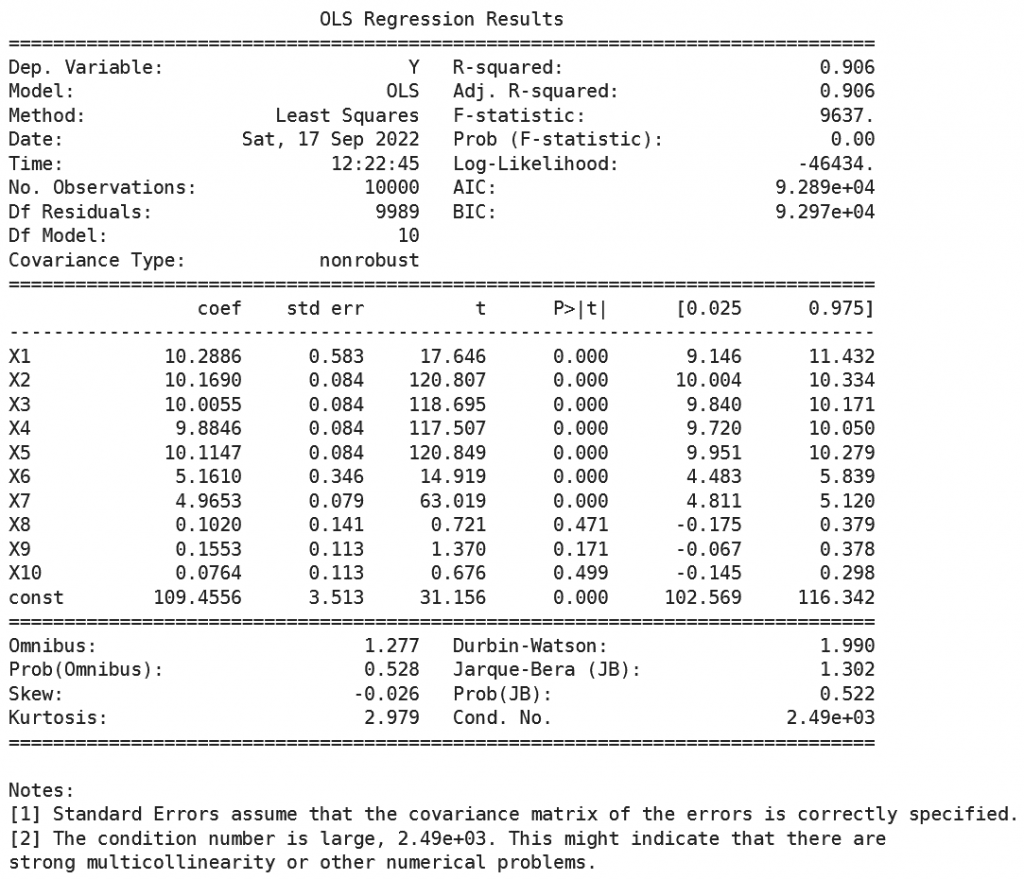
Dengan menggunakan statmodel, diperoleh informasi bahwa model regresi linear memiliki nilai $R^2$ yang tinggi yaitu sebesar 0,906 dimana artinya variabel X yang digunakan mampu menjelaskan sekitar 90% variabel Y.

Selain itu tampak juga variabel $X_8, X_9$ dan $X_{10}$ tidak signifikan. Hal ini sesuai pula dengan rancangan dimana koefisien ketiga variabel ini hanya sebesar 0.1 saja, sangat kecil jika dibandingkan dengan koefisien variabel lainnya.

Berdasarkan nilai koefisien serta adanya indikasi terdapat masalah multikolinearitas menunjukkan data simulasi yang kita bangkitkan seluruhnya sudah sesuai dengan skenario yang dirancang.

• Pembangkitan Bilangan Acak pada Bahasa R
• Membangkitkan Bilangan Acak untuk Sebaran Tertentu dengan Python Numpy
• Sebaran Peubah Acak Diskret
• Model Regresi Logistik untuk Klasifikasi Biner (Implementasi dengan R dan Python)