Association Rules (Teori dan Implementasi dengan Bahasa R)

Association Rules (Aturan Asosiasi) merupakan satu teknik data mining yang digunakan untuk menemukan hubungan menarik atau asosiasi antara kumpulan item dalam dataset besar. Teknik ini sangat populer dalam market basket analysis dan dapat membantu mengidentifikasi pola belanja pelanggan. Informasi yang diperoleh dari Association Rules dapat digunakan untuk berbagai strategi bisnis seperti cross-selling dan promosi produk. Dengan menemukan item-item yang sering dibeli bersama, perusahaan dapat membuat keputusan yang lebih baik terkait penempatan produk, penawaran khusus atau rekomendasi produk serta strategi pemasaran lainnya.

Association rules mencoba untuk menemukan korelasi antara item-item dalam dataset yang disebut sebagai itemset. Itemset dapat terdiri dari satu item tunggal (itemset satu elemen) atau beberapa item (itemset multi-elemen). Aturan asosiasi mengidentifikasi hubungan antara item atau kelompok item dalam bentuk “Jika A, maka B” atau “Jika A dan C, maka D”. Aturan ini menunjukkan seberapa sering dua atau lebih item muncul bersamaan dalam data.

Contoh sederhana association rules adalah “Jika seseorang membeli roti, kemungkinan besar mereka juga akan membeli mentega”. Dalam konteks ini, roti dan mentega adalah item, dan association rules mengidentifikasi pola pembelian bersama yang dapat membantu retailer untuk menyesuaikan strategi mereka, seperti menempatkan roti dan mentega di dekat satu sama lain di rak.

Berikut adalah beberapa kelebihan dan kekurangan dari association rules:

Kelebihan association rules:

1. Kemampuan mengungkapkan hubungan yang tersembunyi: Association rules dapat mengidentifikasi hubungan atau pola yang mungkin tidak terlihat secara langsung dalam data. Informasi ini dapat membantu dalam mengungkapkan wawasan dan pengetahuan baru yang dapat digunakan untuk pengambilan keputusan.
2. Interpretasi yang mudah: Aturan asosiasi secara umum memiliki bentuk yang sederhana dan mudah diinterpretasikan, seperti “Jika X, maka Y”. Hal ini memungkinkan pemahaman yang lebih baik dan pemetaan ke tindakan atau keputusan bisnis yang lebih konkret.
3. Penerapan yang luas: Metode association rules dapat diterapkan dalam berbagai bidang dan industri, seperti e-commerce, pemasaran, pemrosesan bahasa alami, bioinformatika, dan lainnya. Hal ini membuatnya menjadi alat analisis yang serbaguna.
4. Skalabilitas: Algoritma association rules dapat diterapkan pada dataset yang besar dengan efisien. Beberapa algoritma seperti FP-Growth dan Eclat dirancang untuk mengatasi skala dataset yang besar dengan mengurangi kompleksitas komputasi.

Kekurangan association rules:

1. Efek spurious (kesalahan korelasi palsu): Association rules dapat menghasilkan aturan yang terlihat bermakna, tetapi sebenarnya hanya terjadi secara kebetulan atau memiliki korelasi palsu. Hal ini dapat terjadi ketika ada item yang sangat umum dan muncul bersama secara acak.
2. Keterbatasan pada data kualitatif: Association rules lebih umum digunakan untuk data transaksional yang berisi item-item diskrit atau kuantitatif. Data dengan atribut kualitatif atau kontinu dapat memerlukan praproses atau metode lain untuk mengubahnya menjadi bentuk yang cocok untuk analisis association rules.
3. Hanya mengidentifikasi hubungan, bukan kausalitas: Association rules hanya mengungkapkan hubungan statistik antara itemset, bukan hubungan kausal yang sebab-akibat. Dengan kata lain tidak memberikan informasi tentang penyebab di balik hubungan atau mengapa suatu pola terjadi.
4. Sensitif terhadap parameter: Hasil analisis association rules dapat dipengaruhi oleh parameter yang ditentukan seperti batas minimum support dan confidence. Pemilihan parameter yang tidak tepat dapat menghasilkan aturan yang tidak signifikan atau terlalu banyak aturan.
5. Keterbatasan pada data berdimensi tinggi: Ketika dataset memiliki jumlah atribut yang tinggi, analisis association rules dapat menjadi sulit karena ledakan kombinatorial dan kompleksitas komputasi yang tinggi.

Pemahaman akan kelebihan dan kekurangan association rules membantu dalam menggunakan metode ini secara efektif dan menginterpretasikan hasil analisis dengan hati-hati.

Berikut adalah beberapa konsep yang perlu dipahami dalam analisis association rules:

1. Itemset: Sebuah kumpulan item yang muncul bersama sebagai satu kesatuan dalam sebuah transaksi atau dataset. Itemset dapat terdiri dari satu item tunggal (itemset satu elemen) atau beberapa item (itemset multi-elemen).
2. Support (Dukungan): Support adalah ukuran frekuensi atau kejadian suatu itemset dalam dataset. Support dinyatakan sebagai proporsi jumlah transaksi yang mengandung itemset tersebut dibandingkan dengan total jumlah transaksi dalam dataset. Support yang tinggi menunjukkan bahwa itemset tersebut sering muncul bersama dalam data.
3. Confidence (Tingkat Keyakinan): Confidence mengukur seberapa sering aturan asosiasi terbukti benar berdasarkan sejarah data. Dinyatakan sebagai proporsi transaksi yang berisi itemset A dan juga berisi itemset B dibandingkan dengan jumlah transaksi yang hanya berisi itemset A. Confidence yang tinggi menunjukkan bahwa kemungkinan besar itemset B akan muncul jika itemset A juga ada.
4. Lift: Lift adalah ukuran untuk mengukur sejauh mana aturan asosiasi meningkatkan kemungkinan munculnya itemset B jika itemset A terjadi. Lift dihitung sebagai rasio dari tingkat keyakinan aturan dengan tingkat dukungan itemset B. Lift yang lebih besar dari 1 menunjukkan adanya hubungan yang lebih kuat antara itemset A dan itemset B.
5. Support Count: Jumlah absolut transaksi yang mengandung itemset tertentu dalam dataset. Ini merupakan ukuran konkret dari frekuensi itemset dalam data.
6. Candidate Itemset: Kumpulan item yang mungkin menjadi bagian dari aturan asosiasi yang relevan dalam dataset. candidate itemset dibentuk melalui proses eksplorasi dan kombinasi item dari itemset sebelumnya.
7. Minimum Support Threshold: Minimum support threshold adalah ambang batas yang ditentukan sebelumnya untuk menyaring itemset yang memiliki dukungan di atas ambang batas tersebut. Itemset dengan dukungan di bawah ambang batas tersebut dianggap tidak signifikan dan tidak diperhitungkan dalam pembentukan aturan asosiasi.
8. Redundansi: Redundansi terjadi ketika aturan asosiasi memiliki informasi yang tumpang tindih atau sama dengan aturan lainnya. Aturan yang redundan dapat membingungkan dan tidak memberikan pemahaman tambahan yang signifikan.
9. Leverage (Kulminasi): Leverage adalah ukuran yang menghitung seberapa sering suatu aturan asosiasi terjadi di atas batas minimum yang ditentukan. Nilai menunjukkan seberapa signifikan aturan tersebut dibandingkan dengan pengaturan secara acak.
10. Supporting Itemset (Itemset pendukung): Itemset yang terlibat dalam aturan asosiasi tertentu dan mencakup itemset di bagian kiri dan kanan dari aturan tersebut.
11. Predicted Itemset (Itemset yang diprediksi) : Itemset yang muncul bersama berdasarkan aturan asosiasi yang telah ditemukan

Salah satu algoritma yang umum digunakan untuk menemukan aturan asosiasi dalam dataset adalah algoritma Apriori. Algoritma Apriori bekerja dengan prinsip bahwa jika sebuah itemset jarang terjadi dalam dataset, maka subsetnya juga jarang terjadi. Algoritma Apriori mencari secara iteratif candidate itemset, menghitung support, dan membentuk aturan hingga tidak ada lagi candidate itemset yang valid atau tidak ada aturan baru yang memenuhi kriteria seleksi yang ditentukan.

Berikut adalah langkah-angkah pada algoritma apriori :

1. Pembentukan candidate itemset.
   Candidate itemset pertama terdiri dari semua item tunggal yang ada dalam dataset. Kemudian, candidate itemset yang lebih besar dibentuk melalui proses penggabungan antara candidate itemset sebelumnya. Gabungan dilakukan hanya jika subsetnya juga merupakan candidate itemset yang valid berdasarkan prinsip Apriori.
2. Menghitung support.
   Dalam langkah ini, candidate itemset diterapkan pada dataset untuk menghitung support atau frekuensi masing-masing itemset. Candidate itemset yang memiliki dukungan di atas ambang batas minimum yang ditentukan (minimum support threshold) disimpan sebagai itemset pendukung.
3. Pembentukan association rules.
   Dari itemset pendukung yang ditemukan, aturan asosiasi dibentuk dengan menghasilkan kombinasi itemset yang lebih kecil. Aturan asosiasi terbentuk dengan membagi itemset pendukung menjadi itemset pada bagian kiri aturan dan itemset pada bagian kanan aturan. Aturan asosiasi yang terbentuk dievaluasi berdasarkan tingkat keyakinan (confidence) yang dihitung dari dukungan itemset pendukung.
4. Seleksi association rules.
   Association rules yang dibentuk dapat memiliki banyak aturan yang mungkin redundan atau tidak relevan. Oleh karena itu, pada langkah ini dilakukan evaluasi dan seleksi berdasarkan kriteria tertentu, seperti confidence, lift, atau ukuran lain yang relevan. Association rules yang memenuhi kriteria seleksi yang ditetapkan dipilih dan dianggap signifikan.

Selain algoritma Apriori, terdapat juga beberapa algoritma lain yang digunakan untuk menemukan aturan asosiasi, seperti algoritma FP-Growth (Frequent Pattern Growth) dan Eclat (Equivalence Class Transformation). Algoritma-algoritma ini memiliki pendekatan yang sedikit berbeda dalam pencarian itemset pendukung dan pembentukan aturan asosiasi, tetapi tujuannya tetap sama, yaitu mengidentifikasi pola atau hubungan yang signifikan dalam dataset.

Analisis association rules pada bahasa R dapat dilakukan dengan memanfaatkan pustaka arules. Pustaka lain yang dapat digunakan sebagai alat visualisasi hasil analisis yaitu arulesViz. Pada bagian ini kita akan menggunakan kedua pustaka tersebut untuk menganalisis dataset “Groceries” yang juga sudah tersedia pada pustaka arules.

Sebelum masuk ke dalam analisis association rules, kita dapat melihat ringkasan dari data menggunakan fungsi summary. Output yang dihasilkan mencakup jumlah transaksi (baris) yaitu sebanyak 9.835 transaksi serta banyaknya item (kolom) sebanyak 169 item. Selanjutnya ditampilkan pula item-item yang paling sering muncul pada data, dalam contoh ini yaitu “whole milk” yang muncul pada 2.513 transaksi diikuti “other vegetables” sebanyak 1.903 transaksi. Adapun density of 0.02609146 menunjukkan kepadatan matriks adalah 0.026, yang berarti sekitar 2.6% dari semua kemungkinan pasangan item-transaksi adalah bukan nol (item muncul dalam transaksi).

output berikutnya yaitu element (itemset/transaction) length distribution menunjukkan frekuensi transaksi berdasarkan banyaknya item. Misalnya, ada 2.159 transaksi yang hanya memiliki 1 item, 1.643 transaksi dengan 2 item, dan seterusnya.

Labels adalah nama item atau label dari item yang ada dalam transaksi. Contoh dari output di atas adalah frankfurter, sausage, dan liver loaf. Sementara itu, level2 dan level1 menunjukkan kategori hierarkis serta memberikan konteks tambahan tentang item tersebut. level2 merupakan subkategori atau kategori yang lebih spesifik dari item. Misalnya, sausage adalah level2 untuk item seperti frankfurter, sausage, dan liver loaf. Adapun level1 merupakan kategori yang lebih umum atau kategori utama dari item. Misalnya, meat dan sausage adalah level1 yang lebih umum yang mencakup subkategori sausage.

Pada bagian terakhir melalui fungsi inspect dapat dilihat item sesungguhnya pada setiap transaksi (misalkan pada transaksi 1 terdapat 5 item yang dibeli yaitu citrus fruit, semi-finished bread, margarine, dan ready soups)

# Menginstall dan memuat paket
# install.packages("arules")
# install.packages("arulesViz")

library(arules)
library(arulesViz)

# Memuat dataset Groceries
data("Groceries")

# melihat ringkasan data
summary(Groceries)

# menampilkan 5 data transaksi pertama
inspect(Groceries[1:5])

# OUTPUT

transactions as itemMatrix in sparse format with
 9835 rows (elements/itemsets/transactions) and
 169 columns (items) and a density of 0.02609146 

most frequent items:
      whole milk other vegetables       rolls/buns             soda 
            2513             1903             1809             1715 
          yogurt          (Other) 
            1372            34055 

element (itemset/transaction) length distribution:
sizes
   1    2    3    4    5    6    7    8    9   10   11   12   13   14   15   16 
2159 1643 1299 1005  855  645  545  438  350  246  182  117   78   77   55   46 
  17   18   19   20   21   22   23   24   26   27   28   29   32 
  29   14   14    9   11    4    6    1    1    1    1    3    1 

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.000   2.000   3.000   4.409   6.000  32.000 

includes extended item information - examples:
       labels  level2           level1
1 frankfurter sausage meat and sausage
2     sausage sausage meat and sausage
3  liver loaf sausage meat and sausage

[1] {citrus fruit, semi-finished bread, margarine, ready soups}			
[2] {tropical fruit, yogurt, coffee}			
[3] {whole milk}			
[4] {pip fruit, yogurt, cream cheese , meat spreads}			
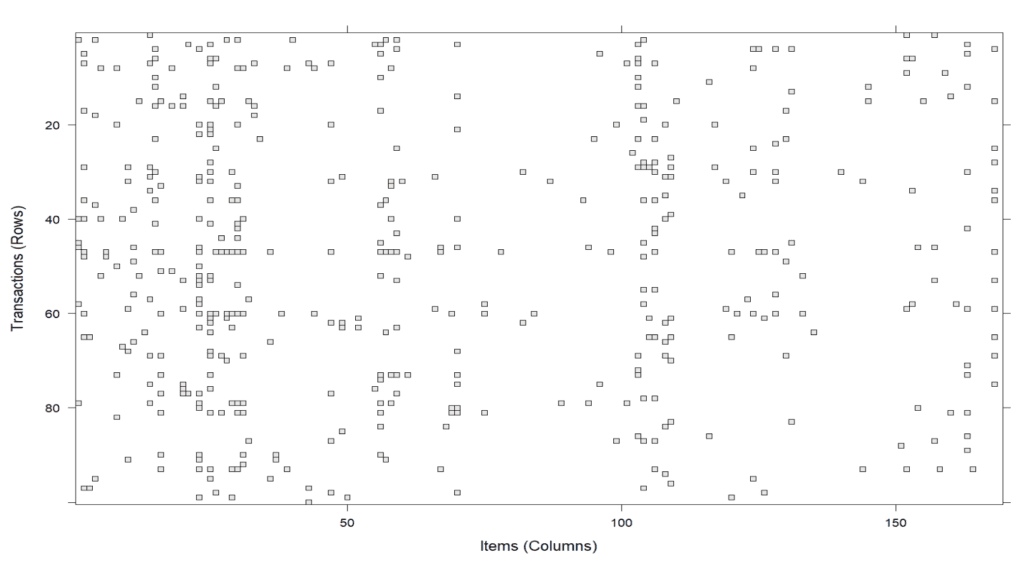
[5] {other vegetables, whole milk, condensed milk, long life bakery product}

Di dalam pustaka arules terdapat fungsi image yang digunakan untuk memvisualisasikan transaksi dan item yang muncul pada transaksi tersebut. Misalkan pada kode image(Groceries[1:5]), fungsi ini memvisualisasikan lima transaksi pertama dari dataset. Hasilnya adalah plot yang menunjukkan item yang ada dalam setiap transaksi dengan penjelasan sebagai berikut:

• Sumbu X: Mewakili lima transaksi pertama (1, 2, 3, 4, 5).
• Sumbu Y: Mewakili item-item yang ada dalam dataset Groceries.
• Kotak: Setiap kotak di dalam plot menunjukkan bahwa item pada sumbu X terdapat dalam transaksi yang ditunjukkan oleh sumbu Y.

R

image(Groceries[1:5])

image(sample(Groceries,100))

Fungsi itemFrequency digunakan untuk memperoleh nilai frekuensi kemunculan suatu item pada keseluruhan transaksi. Secara default nilai yang dikeluarkan berupa nilai relatif banyaknya kemunculan item terhadap banyaknya transaksi. Namun dapat pula diatur jika ingin mendapatkan nilai absolutnya melalui parameter type="absolute".

Berdasarkan hasil di bawah ini diperoleh informasi bahwa item “whole milk” memiliki frekuensi paling tinggi yaitu sebesar 0,2555 diikuti item “other vegetables” dengan frekuensi sebesar 0,1935. Dari seluruh transaksi lebih dari seperempatnya terdapat pembelian item “whole milk” serta sekitar 19,3 persen transaksi terdapat item “other vegetables“.

# Menghitung frekuensi item
item_freq <- itemFrequency(Groceries, type="relative")

item_freq <- sort(item_freq, decreasing = TRUE)

# Menampilkan 5 item dengan frekuensi tertinggi
head(item_freq, 5)

# OUTPUT

whole milk	other vegetables	rolls/buns	soda		yogurt 
0.2555160 	0.1934926        	0.1839349	0.1743772	0.1395018 

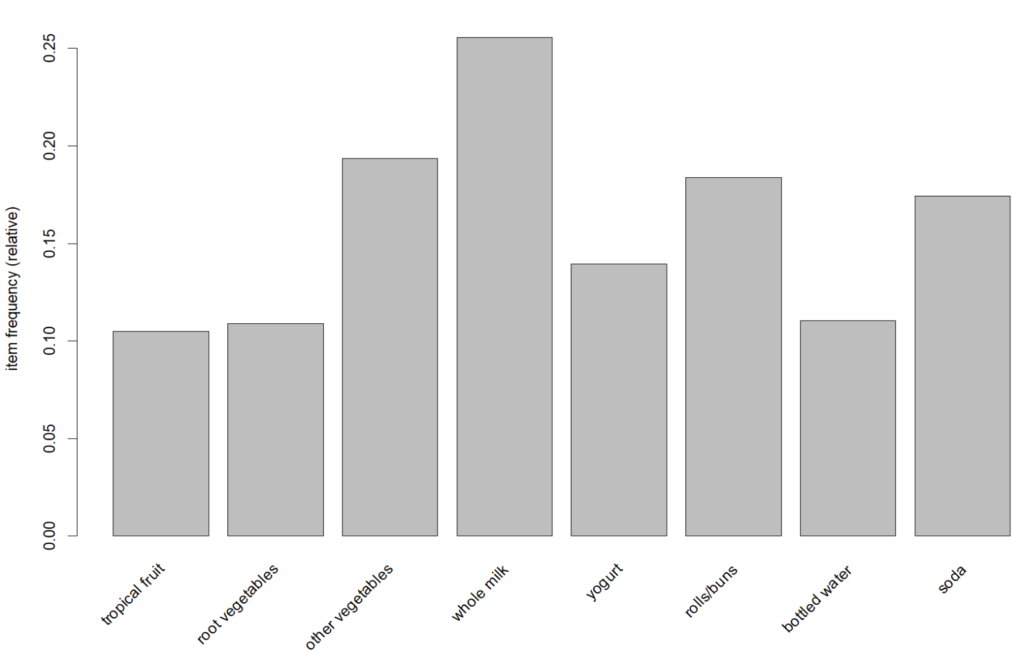
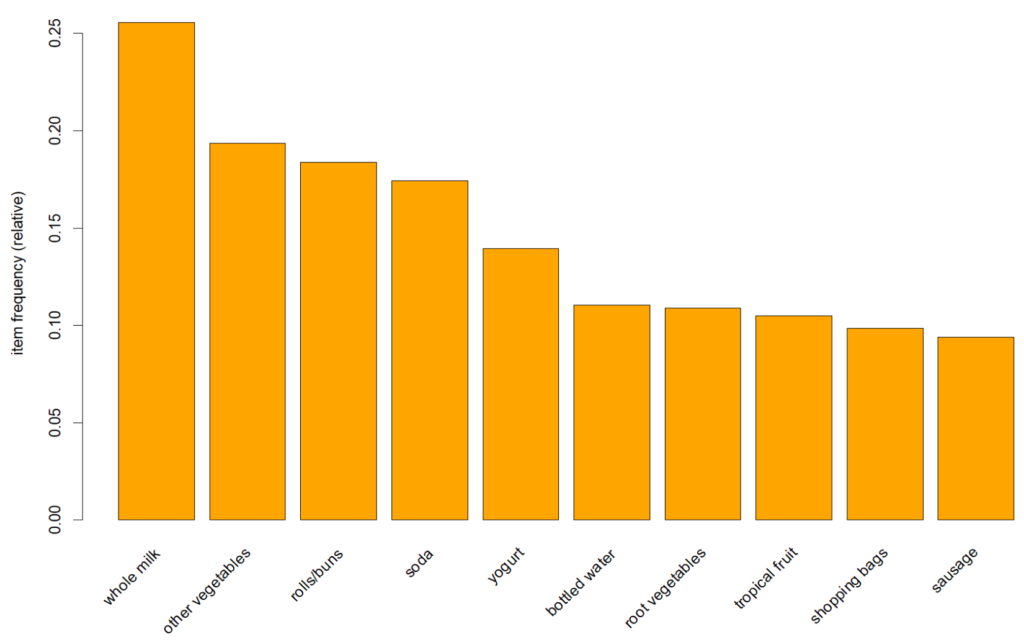
Frekuensi item juga dapat disajikan secara visual menggunakan diagram batang menggunakan fungsii itemFrequencyPlot. Pada fungsi ini kita dapat pula menyaring item yang akan ditampilkan, misal berdasarkan batas nilai support tertentu. Selain itu dapat juga menyajikan n-item dengan nilai terbesar secara berurutan dengan menentukan nilai parameter topN.

R

# menampilkan diagram frekuensi item dengan support >= 0.1
itemFrequencyPlot(Groceries, support=0.1)

# menampilkan diagram frekuensi item 10 item dengan frekuensi terbesar
itemFrequencyPlot(Groceries,topN=10, col="orange")

Seperti yang telah disampaikan pada bagian awal, algoritma apriori merupakan metode yang umum digunakan dalam analisis association rules. Untuk menggunakan metode ini, kita dapat menggunakan fungsi dengan nama yang sama yatu apriori. Terdapat 2 parameter utama pada fungsi ini yaitu data dan parameter. Parameter data merupakan dataset yang akan dianalisis, dalam contoh ini yaitu dataset Groceries. Adapun pada parameter parameter kita dapat menentukan beberapa nilai batas misalkan untuk support dan confidence. Dengan pengaturan ini, maka rules dengan nilai support dan confidence yang lebih rendah dari batas tertentu tidak akan disertakan pada rules-rules yang terbentuk.

Dari output di bawah, kita peroleh total sebanyak 171 rules yang memenuhi kriteria nilai support dan confidence yang ditetapkan.

Output “rule length distribution (lhs + rhs):sizes” memberikan distribusi panjang association rules yang dihasilkan oleh algoritma Apriori. Penjelasan lengkapnya adalah sebagai berikut:

• rule length distribution (lhs + rhs): Ini merujuk pada panjang atau jumlah item pada kedua sisi association rules yang dihasilkan, yaitu sisi kiri (lhs) dan sisi kanan (rhs) dari rules.
• sizes: Ini menunjukkan jumlah rules untuk setiap panjang rules tersebut.

Dalam output ini, terdapat tiga kategori panjang aturan: 1, 2, dan 3.

• Ada 1 aturan yang memiliki 1 item pada kedua sisi (lhs dan rhs). Ini berarti aturan tersebut hanya terdiri dari satu item.
• Ada 96 aturan yang memiliki 2 item pada kedua sisi (lhs dan rhs). Ini berarti aturan-aturan ini terdiri dari dua item, satu pada sisi kiri dan satu pada sisi kanan.
• Ada 74 aturan yang memiliki 3 item pada kedua sisi (lhs dan rhs). Ini berarti aturan-aturan ini terdiri dari tiga item, beberapa pada sisi kiri dan beberapa pada sisi kanan.

Selain itu terdapat beberapa ringkasan statistik mengenai berbagai ukuran dalam association rules yang dihasilkan.

# Membuat aturan asosiasi menggunakan algoritma Apriori
association_rules <- apriori(data=Groceries, parameter = list(support = 0.01, confidence = 0.25))

summary(association_rules)

# OUTPUT

Apriori

Parameter specification:

Algorithmic control:

Absolute minimum support count: 98 

set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
sorting and recoding items ... [88 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 3 4 done [0.00s].
writing ... [171 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].
set of 171 rules

rule length distribution (lhs + rhs):sizes
 1  2  3 
 1 96 74 

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.000   2.000   2.000   2.427   3.000   3.000 

summary of quality measures:
    support          confidence        coverage            lift            count       
 Min.   :0.01007   Min.   :0.2517   Min.   :0.01729   Min.   :0.9932   Min.   :  99.0  
 1st Qu.:0.01159   1st Qu.:0.2965   1st Qu.:0.03101   1st Qu.:1.5175   1st Qu.: 114.0  
 Median :0.01454   Median :0.3582   Median :0.04291   Median :1.7716   Median : 143.0  
 Mean   :0.01961   Mean   :0.3697   Mean   :0.05741   Mean   :1.8695   Mean   : 192.9  
 3rd Qu.:0.02115   3rd Qu.:0.4252   3rd Qu.:0.05877   3rd Qu.:2.1412   3rd Qu.: 208.0  
 Max.   :0.25552   Max.   :0.5862   Max.   :1.00000   Max.   :3.2950   Max.   :2513.0  

mining info:
      data ntransactions support confidence
 Groceries          9835    0.01       0.25

Selanjutnya, kita dapat juga menyeleksi rules-rules berdasarkan kriteria tertentu misalkan berdasarkan nilai support, confidence, lift dan sebagainya. Pada contoh di bawah ini, kita mengambil 10 rules yang memiliki nilai confidence tertinggi. Hasil yang diperoleh yaitu rules {citrus fruit, root vegetables} => {other vegetables} memiliki nilai confidence tertinggi sebesar 0,5862. Rules ini menyatakan bahwa jika seseorang membeli citrus fruit dan root vegetables maka orang tersebut juga cenderung akan membeli item other vegetables. Pada konteks ini berarti sekitar 58,6 persen yang membeli citrus fruit dan root vegetables juga membeli other vegetables.

Sementara itu, support adalah 0.01037112 berarti 1,037% dari semua transaksi dalam dataset memenuhi syarat untuk rule ini. Nilai coverage 0.01769, yang berarti 1.769% dari semua transaksi dalam dataset mengandung setidaknya citrus fruit dan root vegetables. Adaapun nilai lift pada rule tersebut sebesar 3.029608, yang menunjukkan bahwa kemungkinan pembelian other vegetables ketika pelanggan membeli citrus fruit dan root vegetables adalah sekitar 3,03 kali lebih tinggi dibandingkan pembelian acak.

# Menampilkan aturan dengan support dan confidence tertinggi
top_rules <- head(sort(association_rules, by = "confidence", decreasing = TRUE), 10)
​
inspect(top_rules)

# OUTPUT

lhs                                       rhs                support     confidence coverage   lift     count
[1]  {citrus fruit, root vegetables}   => {other vegetables} 0.01037112  0.5862069  0.01769192 3.029608 102  
[2]  {tropical fruit, root vegetables} => {other vegetables} 0.01230300  0.5845411  0.02104728 3.020999 121  
[3]  {curd, yogurt}                    => {whole milk}       0.01006609  0.5823529  0.01728521 2.279125  99 
...
[8]  {yogurt, whipped/sour cream}      => {whole milk}       0.01087951  0.5245098  0.02074225 2.052747 107 
[9]  {root vegetables, rolls/buns}     => {whole milk}       0.01270971  0.5230126  0.02430097 2.046888 125  
[10] {pip fruit, other vegetables}     => {whole milk}       0.01352313  0.5175097  0.02613116 2.025351 133

Jika diperlukan, kita juga dapat mengambil informasi terkait ukuran yang diperoleh pada setiap rule menggunakan fungsi quality seperti yang disajikan pada kode berikut ini.

# Menghitung metrik support, confidence, dan lift
rule_metrics <- quality(top_rules)
rule_metrics_df <- as.data.frame(rule_metrics)

# Menampilkan metrik untuk aturan teratas
head(rule_metrics_df, 10)

# OUTPUT

	   support	   confidence   coverage	  lift		count 
118	0.01037112	0.5862069	0.01769192	3.029608	102
128	0.01230300	0.5845411	0.02104728	3.020999	121
 98	0.01006609	0.5823529	0.01728521	2.279125	 99
102	0.01148958	0.5736041	0.02003050	2.244885	113
131	0.01199797	0.5700483	0.02104728	2.230969	118
146	0.01453991	0.5629921	0.02582613	2.203354	143
104	0.01230300	0.5525114	0.02226741	2.162336	121
110	0.01087951	0.5245098	0.02074225	2.052747	107
152	0.01270971	0.5230126	0.02430097	2.046888	125
114	0.01352313	0.5175097	0.02613116	2.025351	133

Kita dapat pula mencari rules yang secara spesifik mengandung item tertentu menggunakan fungsi subset. Contoh kode berikut ini menunjukkan daftar rules yang mengandung item “berries“.

berryrules<-subset(association_rules, items %in% "berries")
inspect(berryrules)

# OUTPUT

   lhs          rhs                support    confidence coverage  lift     count
[1] {berries} => {yogurt}           0.01057448 0.3180428  0.0332486 2.279848 104
[2] {berries} => {other vegetables} 0.01026945 0.3088685  0.0332486 1.596280 101 
[3] {berries} => {whole milk}       0.01179461 0.3547401  0.0332486 1.388328 116

Penyajian hasil analisis dapat dibuat dalam bentuk visualisasi melalui fungsi plot. Terdapat beberapa jenis visualisasi yang dapat digunakan dengan mengatur parameter method yaitu "scatterplot", "two-key plot", "matrix", "matrix3D", "mosaic", "doubledecker", "graph", "paracoord" atau "grouped", dan "iplots". Parameter lainya yang penting yaitu measure yang dapat ditentukan sesuai ukuran yang menjadi fokus misal "support", "confidence", "lift", dan "order".

R

# visualisasi dengan graph
plot(top_rules, method = "graph", measure = "confidence")

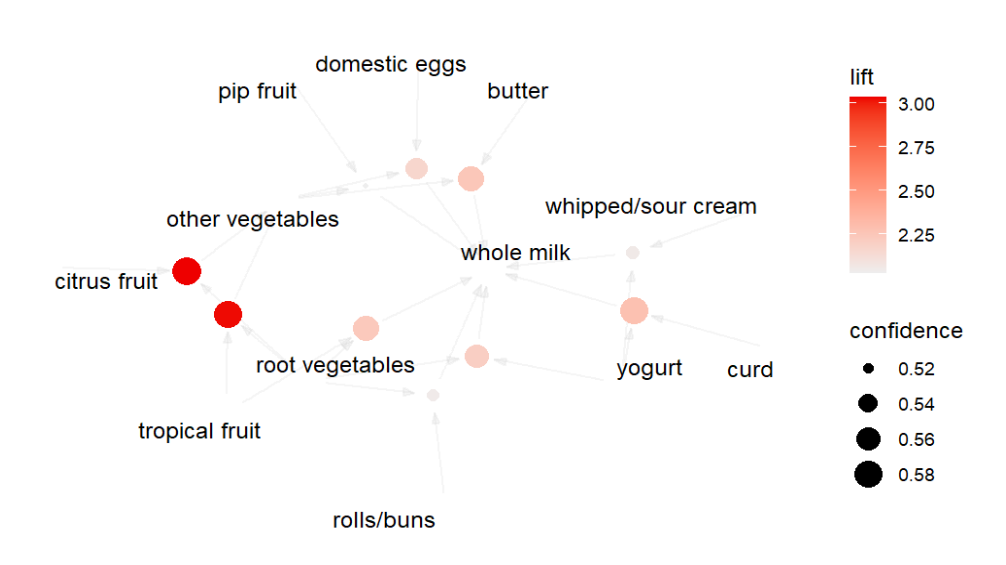
R

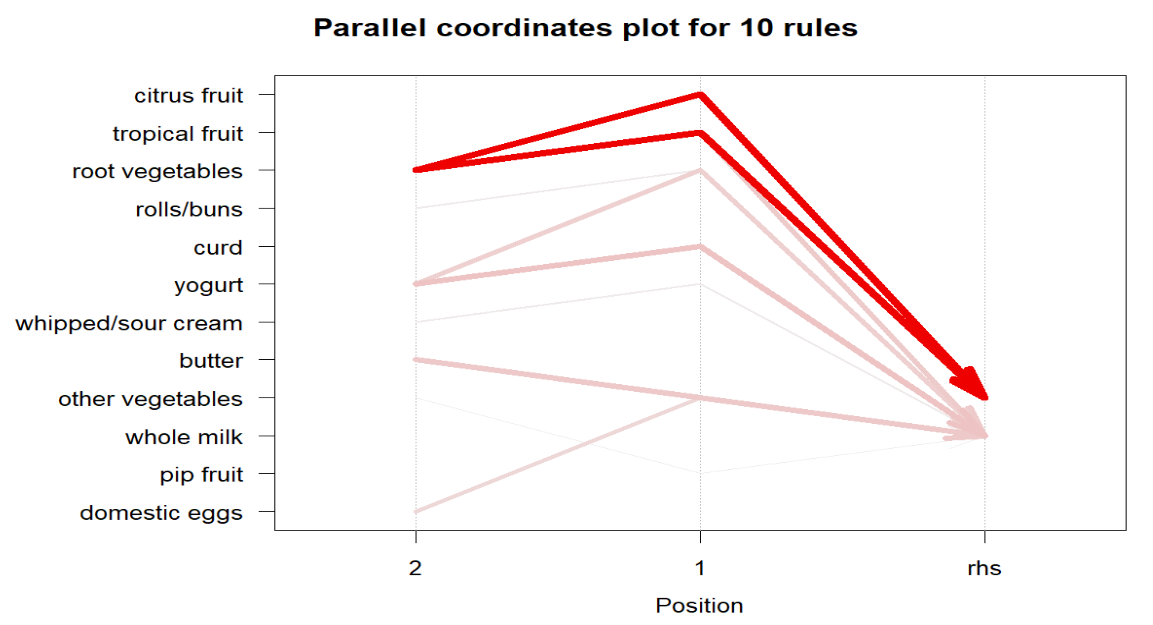
# Visualisasi dengan parallel coordinates plot
plot(top_rules, method = "paracoord", , measure = "confidence")

(Cahya Alkahfi dan Rizki Ananda)

• Ananda, R. (2023). RPubs – STA1382 Association Rules
• Anisa, R. (2023). RPubs – Association Rules
• Lantz, B. (2013). Machine learning with R: learn how to use R to apply powerful machine learning methods and gain an insight into real-world applications. Packt Publishing.