Resampling Bootstrap untuk Pendugaan Parameter Menggunakan Python


Bootstrap Resampling
Di dalam statistika, bootstrap adalah metode penarikan sampel dengan pengembalian berulangkali dari sekumpulan data sampel yang berasal dari populasi tertentu. Tujuan utama bootstrap resampling adalah untuk meningkatkan jumlah sampel dari sampel asli dengan harapan menghasilkan nilai dugaan parameter populasi yang lebih baik. Metode bootstrap sering digunakan pada populasi dimana sebarannya tidak diketahui. Informasi yang dimiliki hanya berdasarkan sampel yang tersedia, sehingga sampel tersebut dikondisikan seolah-olah sebagai populasi untuk menduga parameter. Selain itu metode bootstrap juga digunakan pada beberapa algoritma machine learning seperti bagging dan random forest.
lihat : Random Forest untuk Model Klasifikasi Menggunakan Scikit-Learn
Kunci dari bootstrap adalah melakukan sampling dengan pengembalian berulang kali. Selanjutnya dari hasil setiap ulangan akan diperoleh nilai penduga (misal mean, median, koefisien regresi dan lain sebagainya) yang membentuk suatu sebaran empirik dengan harapan mampu menggambarkan parameter populasi yang sebenarnya. Adapun nilai dari penduga ditentukan berdasarkan rata-rata dari nilai penduga pada setiap ulangan.


Pada ilustrasi di atas terdapat suatu populasi yang tidak diketahui sebarannya. Informasi yang dimiliki hanya dari 10 sampel saja. Dari sini, kita bisa menggunakan metode bootstrap untuk menduga nilai parameter populasinya (misalkan mean, median dan standar deviasi).
Langkah-langkah yang perlu dilakukan adalah sebagai berikut:
- Ambil sampel sebanyak n dengan pengembalian dari data sampel asli. Karena menggunakan pengembalian, maka 1 amatan dari sampel asli dapat terpilih berkali-kali. Sebagai contoh pada ulangan ke-1 angka 112 dan 120 masing-masing terpilih sebanyak 2 kali.
- Ulangi penarikan sampel seperti pada langkah ke-1 sebanyak B kali. Jumlah yang diperlukan umumnya memerlukan ulangan yang relatif banyak dengan harapan sebaran data semakin menggambarkan kondisi sebenarnya. Dengan bantuan komputer saat ini, menggunakan nilai B yang sangat besar ratusan bahkan sampai ribuan kali dapat ditangani dengan mudah.
- Selanjutnya dari data pada setiap ulangan, hitung penduga parameternya. Sebagai contoh untuk ulangan pertama diperoleh rata-rata = 118.2 atau untuk penduga median adalah 119.
- Langkah berikutnya, nilai penduga akhir dihitung berdasarkan nilai rata-rata dari semua nilai penduga yang didapat pada langkah 3.
Nilai rata-rata dari penduga untuk setiap ulangan :
$$\bar{\hat{\theta}}=\frac{1}{B}\sum_{i=1}^B \hat{\theta}^{(i)}$$
Adapun ragam/varians dari penduga dapat dihitung menggunakan :
$$Var(\bar{\hat{\theta}})=\frac{1}{B-1}\sum_{i=1}^B (\hat{\theta}^{(i)}-\bar{\hat{\theta}})^2$$
Selain itu, berdasarkan hasil bootstrap juga dapat digunakan untuk memperoleh selang kepercayaan bagi parameter yaitu dengan menetapkan batas kuantil (misal interval 95% pada selang 2,5% – 97.5%) dari hasil yang diperoleh.
Implementasi Bootstrap dengan Python
Sekarang, kita akan mencoba mengimplementasikan metode bootstrap menggunakan python. Terdapat beberapa hal yang akan dilakukan dalam implementasi ini. Pertama adalah membangkitkan populasi fiktif yang mengikuti sebaran tertentu. Pembangkitan ini semata-mata dilakukan agar nanti dapat membandingkan dugaan parameter hasil bootstrap dengan nilai aslinya. Sehingga dapat melihat seberapa dekat hasil bootstrap dalam menduga nilai parameter pada contoh data tersebut.
Membangkitkan Data Simulasi Populasi
Misalkan di kota F terdapat 10.000 rumah tangga, dimana besarnya pendapatan setiap rumah tangga mengikuti sebaran $Gamma(\alpha=10, \beta=1000)$. Besarnya pendapatan dari setiap rumah tangga akan kita bangkitkan secara acak sesuai dengan sebarannya.
lihat : Pembangkitan Bilangan Acak pada Bahasa R
Python
# memuat library yang diperlukan
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# membuat objek randomstate
# agar angka random yang dihasilkan selalu sama
randomstate = np.random.RandomState(10)
# Membangkitkan 10000 data populasi fiktif
# menyebar Gamma dengan alpha=10, Beta=2000
pop = randomstate.gamma(shape=10, scale = 1000, size=10000)
pop = np.round(pop, 2)
# Histogram data populasi
sns.set(rc = {'figure.figsize':(15,8)})
plot = sns.histplot(data=pop, bins=30, color="green")
plot.set(xlim=(0,25000))
# Menghitung rata-rata dan median populasi
print(f'mean : {round(np.mean(pop), 1)}')
print(f'median : {round(np.median(pop), 1)}')Output
# Output (Populasi) mean : 10038.7 median : 9735.5

Fungsi RandomState digunakan agar setiap kali menjalankan kode, dapat menghasilkan angka random yang sama, begitu juga jika mengeksekusi kode dari perangkat lain, selama nilai RandomState sama maka angka acak yang dihasilkan akan selalu sama.
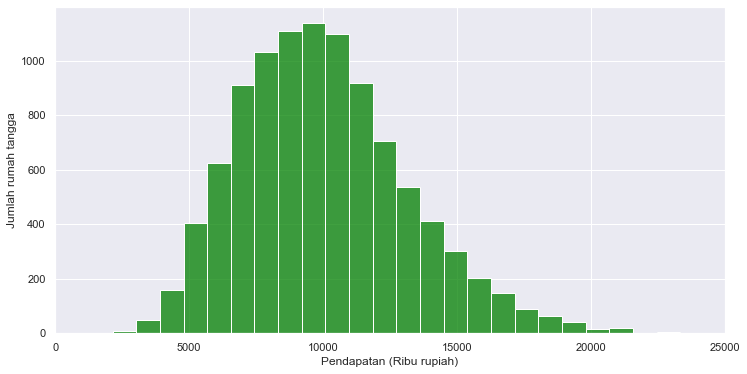
Dari histogram di atas, telihat bagaimana sebaran besaran pendapatan dari populasi kota F, dimana sebagian besar data memusat pada kisaran 10.000 dengan kecenderungan menceng ke kanan. Hal ini berarti Dari data tersebut diketahui pula bahwa rata-rata pendapatan dari seluruh penduduk adalah 10.038,7. Selanjutnya median dari data populasi sebesar 9.735,5 dimana artinya setengah rumah tangga memiliki pendapatan kurang dari 9.978,7 dan setengahnya lagi lebih besar dari 9.673,3.
Perlu diingat data populasi ini digunakan semata-mata sebagai bahan perbandingan hasil pendugaan metode bootstrap, informasi nilai parameter pada kenyataannya hampir tidak pernah diketahui.
Penarikan Sampel
Misalkan dari 10.000 populasi tersebut kita mampu menarik sampel acak sebanyak 20. Informasi yang kita miliki pada dasarnya hanya berasal dari 20 sampel ini.
Python
# membuat objek randomstate
# agar angka random yang dihasilkan selalu sama
rs = np.random.RandomState(123)
# menarik sampel acak sebanyak 20
sampel = rs.choice(pop, 20, replace=False)
print(sampel)
# Menghitung rata-rata dan median sampel
print(f'mean : {round(np.mean(sampel), 1)}')
print(f'median : {round(np.median(sampel), 1)}')Output
# Output [ 7601.53 5936.26 10341.92 11919.38 8973.8 11970.96 9735.39 9375.18 10986.31 8564.36 16300.8 7168.36 17681. 9225.43 3434.29 18596.29 11590.88 7074.76 6155.92 9286.57] mean : 10096.0 median : 9330.9
Dari hasil perhitungan 20 sampel tersebut, nilai rata-rata pendapatan sebesar 10.096,0 dan median sebesar 9.330,9. Mengingat banyaknya jumlah populasi, sangat mungkin hasil pendugaan berdasarkan 20 sampel masih kurang baik. Selain itu, kita juga sulit mendapatkan selang kepercayaan bagi nilai dugaan parameter seperti median dan standar deviasi dimana sebarannya tidak diketahui. (Adapun untuk rata-rata, sebarannya akan mengikuti sebaran normal, sehingga penghitungan selang kepercayaan dapat menggunakan pedekatan Normal).
Selanjutnya data 20 sampel ini akan menjadi basis untuk menduga nilai parameter menggunakan metode bootstrap.
Sekali lagi perlu diingat data populasi ini dan informasi nilai parameter pada kenyataannya hampir tidak pernah diketahui. Tujuan pendugaan parameter adalah untuk memperkirakan suatu nilai yang belum diketahui. Jika nilai parameter sebenarnya diketahui maka tidak ada gunanya lagi melakukan pendugaan.
Proses Bootstraping
Pada langkah ini , kita melakukan penarikan sebanyak 20 sampel acak dengan pengembalian berdasarkan 20 sampel acak awal yang dimiliki. Proses penarikan sampel diulang sebanyak nilai B tertentu, misalkan sebanyak 5.000 kali.
Penarikan sampel dengan pengembalian dapat menggunakan method choice pada objek RandomState.
Python
# membuat objek numpy array
# menyimpan data untuk 5000 ulangan bootstrap
# masing-masing ulangan memiliki 20 sampel
samples_boots = np.zeros((5000, 20))
rs = np.random.RandomState(123)
# melakukan bootstrap sebanyak 5000 kali
for i in range(5000):
# ambil 20 sampel dengan pengembalian
samples_boots[i] = rs.choice(sampel, size=20, replace=True)
# 20 sampel pada ulangan ke-1
print(samples_boots[0])
# 20 sampel pada ulangan ke-2
print(samples_boots[1])Output
# Output (data ulangan 1 dan 2) [ 9225.43 10341.92 10341.92 9735.39 7074.76 9286.57 16300.8 5936.26 7601.53 7074.76 18596.29 8564.36 7601.53 3434.29 7601.53 18596.29 9286.57 3434.29 8973.8 7601.53] [11590.88 8973.8 7074.76 11919.38 10341.92 9375.18 10341.92 18596.29 11590.88 9375.18 8564.36 11919.38 9735.39 5936.26 10341.92 5936.26 17681. 10986.31 11919.38 16300.8 ]
Dari kode di atas, kita melakukan proses boootstrap dengan 5000 ulangan. Oleh karena itu sekarang kita memiliki 5000 dataset dengan masing-masing terdiri dari 20 sampel. Karena merupakan penarikan sampel dengan pengembalian, maka sampel pada setiap ulangan adalah angka-angka yang sama seperti 20 sampel asli, hanya saja ada beberapa elemen yang sama dan ada beberapa elemen yang tidak terpilih.
Pendugaan Parameter
Seperti yang sudah disampaikan di awal, untuk melakukan pendugaan parameter dari data bootsrap kita perlu menghitung rata-rata hasil dari setiap ulangan. Untuk menentukan penduga nilai tengah maka hitung rata-rata dari nilai rata-rata sampel setiap ulangan . Begitu juga untuk penduga median, diperoleh dengan menghitung rata-rata (bukan median) dari nilai median setiap ulangan.
Python
# Menghitung nilai rata-rata setiap ulangan mean_boots = np.mean(samples_boots, axis=1) # menghitung nilai median setiap ulangan med_boots = np.median(samples_boots, axis=1) print(mean_boots) print(med_boots)
Output
# Nilai rata-rata dan median 20 sampel untuk setiap ulangan [ 9330.491 10925.0625 10005.552 ... 11496.007 9430.8165 10957.8345] [ 8769.08 10341.92 9330.875 ... 10341.92 9130.185 9555.285]
Menurut hasil di atas, nilai rata-rata pada ulangan pertama sebesar 9.330,491, rata-rata pada ulangan kedua 10.925,0625 dan seterusnya. Begitu juga untuk nilai median, median pada ulangan pertama adalah 8.769,08, ulangan kedua 10.341,92 dan seterusnya.
Untuk memperoleh penduga parameter (rata-rata dan median) maka kita hitung rata-rata nilai penduga dari setiap ulangan.
Python
# menghitung penduga rata-rata#
mean_est = np.mean(mean_boots)
# menghitung penduga median
med_est = np.mean(med_boots)
print("Penduga Rata-rata:", mean_est)
print("Penduga median:", med_est)Output
# Output Penduga Rata-rata: 10091.571506999999 Penduga median: 9504.16594
Dari sampel hasil bootstrap, dugaan nilai tengah bagi populasi sebesar 10.091,57 berbanding nilai aslinya sebesar 10.038,7 (lagi-lagi dalam kenyataan, nilai ini umumnya tidak diketahui). Adapun untuk median nilai penduga yang diperoleh sebesar 9.504,16 berbanding nilai aslinya sebesar 9.735,5. Hasil ini tentu saja bisa berbeda-beda tergantung pada sampel acak yang diambil saat proses bootstrap.
Kita juga dapat mengukur nilai standar deviasi bagi penduga rata-rata dan median.
Python
print(f'std(mean) : {round(np.std(mean_boots), 1)}')
print(f'std(med) : {round(np.std(med_boots), 1)}')Output
# Output # std(mean) : 840.0 # std(med) : 734.5
Interval Kepercayaan
Kegunaan lainnya dari bootstrap yaitu untuk melihat selang kepercayaan, khususnya bagi parameter seperti median, dimana sebarannya tidak diketahui.
Python
plt.rcParams["figure.figsize"] = [12, 6]
plt.rcParams["figure.autolayout"] = True
f, axes = plt.subplots(1, 2)
plt_mean = sns.histplot(data=mean_boots, bins=30, color="orange", ax=axes[0])
plt_mean.set(xlabel="Mean",
ylabel="Jumlah rumah tangga")
plt_med = sns.histplot(data=med_boots, bins=30, color="orange", ax=axes[1])
plt_med.set(xlabel="Median",
ylabel="Jumlah rumah tangga")
plt.show()Output
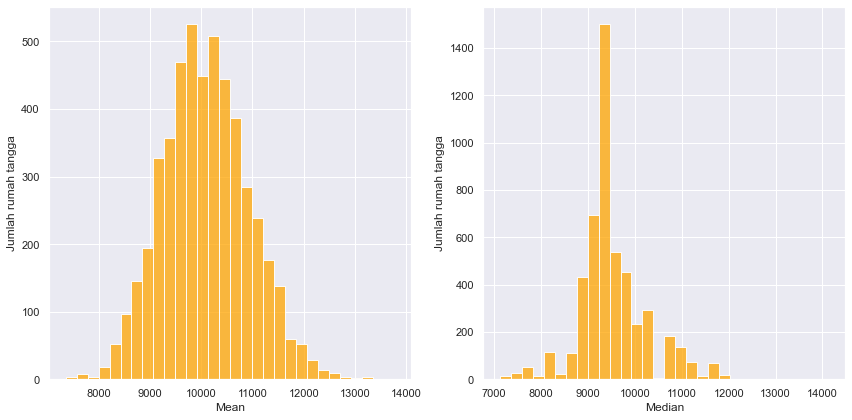

Gambar di atas merupakan histogram distribusi nilai dugaan bagi nilai tengah dan median menurut 5000 ulangan bootstrap.
Untuk mendapatkan selang kepercayaan 95% bagi nilai tengah dan median berdasarkan hasil bootstrap dapat menggunakan fungsi quantile yang tersedia pada numpy.
Python
print(f'LB (mean) : {round(np.quantile(mean_boots, 0.025), 1)}')
print(f'UB (mean) : {round(np.quantile(mean_boots, 0.975), 1)}')
print(f'LB (med) : {round(np.quantile(med_boots, 0.025), 1)}')
print(f'UB (med) : {round(np.quantile(med_boots, 0.975), 1)}')Output
# Output LB (mean) : 8530.0 UB (mean) : 11788.4 LB (med) : 8082.9 UB (med) : 11288.6
Selang kepercayaan 95% bagi rata-rata adalah 8.530,0 - 11.788,4 dan selang kepercayaan 95% bagi median adalah 8.082,9 - 11.288,6.
Demikian penjelasan mengenai implementasi algoritma resampling bootstrap menggunakan python. Semoga dapat menambah pemahaman bagaimana algoritma bootstrap bekerja.
Referensi
- Efron, B dan Tibshirani, R. (1993). An Introduction to the Bootstrap. Boca Raton, FL: Chapman & Hall/CRC.
- James, G., Witten, D., Hastie, T., Tibshirani, R. 2014, An Introduction to Statistical Learning with Applications in R, Springer.
- https://www.journaldev.com/45580/bootstrap-sampling-in-python
- https://towardsdatascience.com/bootstrapping-using-python-and-r-b112bb4a969e








