Pembangkitan Bilangan Acak pada Bahasa R

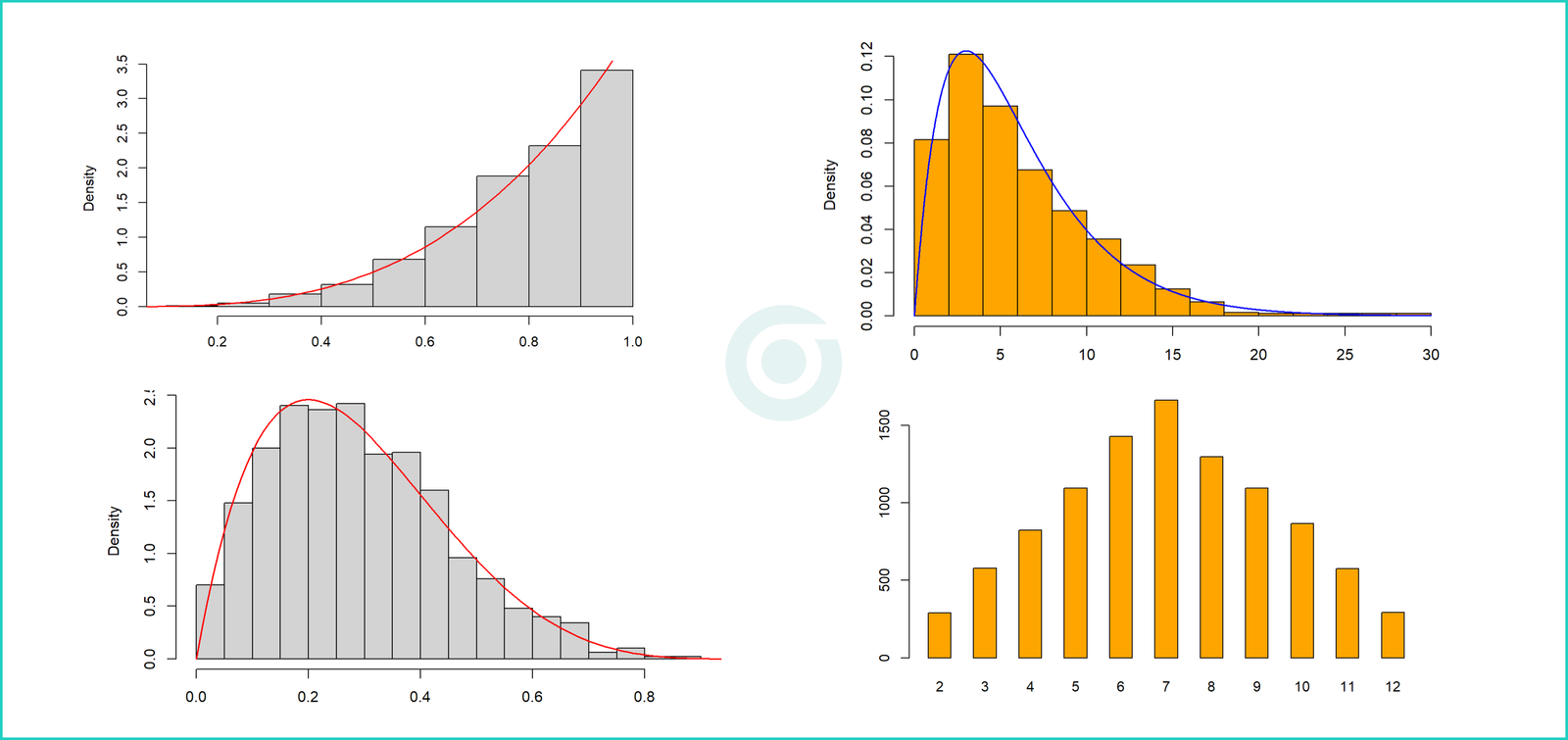
Pembangkitan bilangan acak merupakan teknik yang umum dalam bidang Statistika. Pembangkitan biasanya dilakukan untuk membuat sejumlah angka acak yang mengikuti distribusi peluang tertentu. Teknik ini dapat digunakan sebagai data simulasi pada model-model statistik tertentu sebelum penerapannya pada data real yang diperoleh dari hasil observasi, percobaan maupun cara lainnya.

Di dalam bahasa pemrograman seperti R, bilangan acak ini juga disebut dengan pseudorandom atau bilangan acak semu. Hal tersebut karena kita dapat menentukan nilai seed tertentu sehingga bilangan acak yang dihasilkan dapat direproduksi dengan nilai-nilai yang persis sama. Reproduksi ini penting untuk melakukan pengujian kembali misalkan pengecekan hasil yang didapatkan dari penelitian orang lain. Jika bilangan acak yang dibangkitkan terus menerus berubah, maka hampir mustahil untuk memperoleh hasil pengujian yang sama karena data yang dibangkitkan juga berbeda.

Pada tulisan ini kita akan membahas 4 cara yang bisa digunakan untuk melakukan pembangkitan bilangan acak yaitu:

• MenggunakanFungsi Built-In pada R
• Metode Inverse-Transform
• Metode Acceptance-Rejection
• Metode Transformasi Peubah Acak

Bahasa R menyediakan fungsi built-in untuk membangkitkan bilangan acak. Terdapat dua contoh yang akan kita buat, yaitu sebaran Gamma dan sebaran binomial menggunakan fungsi r.... Silahkan mengeksplorasi contoh untuk sebaran lainnya.

Selain membangkitkan bilangan acak dari sebaran tersebut, kita juga akan memvisualisasikan untuk membandingkan sebarand ari bilangan acak yang dibangkitkan (empiris) terhadap fungsi peluang teoritisnya. Hasil tersebut akan menunjukkan apakah data yang kita bangkitkan benar-benar mengikuti sebaran teoritisnya.

Membangkitkan 1000 bilangan acak yang menyebar $Gamma(\alpha = 2, \beta = 3)$ menggunakan fungsi rgamma:

# buat seed dengan angka sembarang
# penggunaan seed yang sama untuk tujuan reproduksi hasil
set.seed(1)

# Membangkitkan 1000 bilangan acak Gamma(alpha=2, beta=3)
data.rand <- rgamma(1000, shape = 2, rate = 1/3)

data.rand

# OUTPUT

   [1]  2.49259501 10.71226904 10.38951114  6.15243555 11.65622709  7.62162072
   [7]  6.86419890  3.44787797  2.04306440  2.50687125  3.46776072  4.33641765
  [13]  1.81951499  8.02316253  6.94667188  8.50992803  7.83255516  4.77813920
  [19] 11.57299378  9.37354270  2.31933639  2.91463512  3.67562700  4.13025776
  ...
 [973]  1.29443608 12.36527415  3.66358552  3.66571312 10.75322356  3.93716428
 [979]  6.31458530  8.66805706  1.14792501  5.54578405  2.84170609  1.55323681
 [985]  3.33537513  1.14813035  5.73024444  7.92705430  6.46308436 13.07328688
 [991]  4.88423173  1.59793943  5.67557601  9.44653117  9.53071418  5.24736176
 [997] 10.81894507  5.01317125 12.02366922  4.00413010

Data yang sudah dibangkitkan dapat divisualisasikan dalam bentuk histogram seperti berikut:

# Membuat histogram dari data.rand
hist(data.rand, prob = T, breaks = 20)

# Membuat grafik kurva gamma(alpha = 2, beta = 3)
# batas atasnya disesuaikan agar lines-nya terlihat, misal 0-30
x.axis <- seq(0, 30, .01)

# Menghitung nilai pdf untuk setiap x pada x.axis
y.axis <- dgamma(x=x.axis, shape = alpha, rate = 1/beta)

lines(x.axis, y.axis, col="red", lwd=1.5)

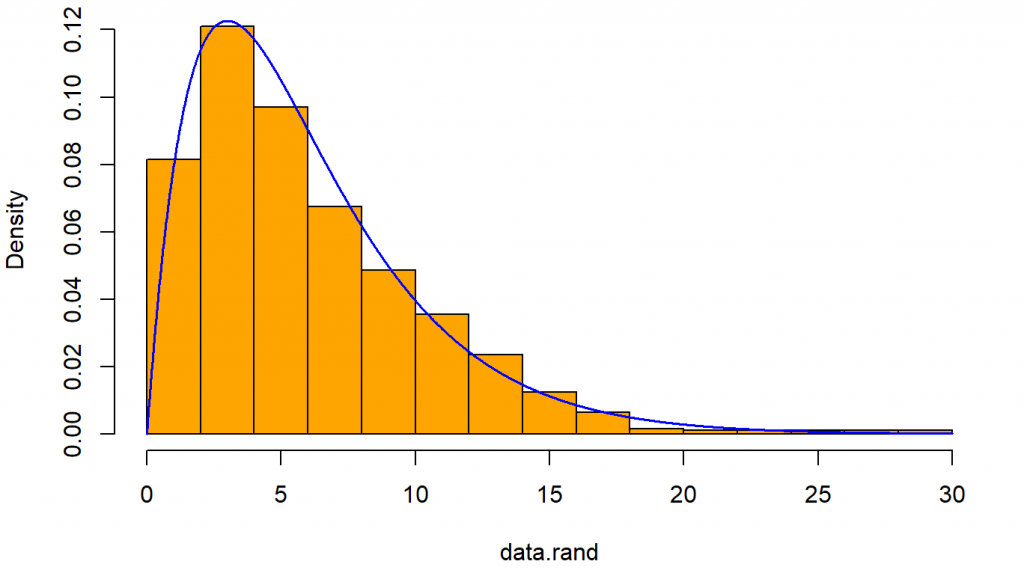
Gambar di atas menyajikan histogram dari 1000 bilangan acak hasil pembangkitan. Selain itu kita sandingkan dengan kurva fungsi sebaran teoritisnya yaitu $Gamma(\alpha=2, \beta=3)$. Dapat terlihat bahwa sebaran bilangan acak yang diperoleh sudah sesuai dengan sebaran teoritisnya.

Silahkan mencoba dengan jumlah angka acak berbeda atau nilai parameter $\alpha$ dan $\beta$ yang berbeda. Secara teori, semakin banyak data yang kita bangkitkan maka akan menghasilkan bentuk yang semakin mirip sebaran teoritisnya.

Pada contoh ini, kita akan membangkitkan data yang mengikuti sebaran diskret. Misalkan sebaran $Binomial(n = 8, p = 0.25)$ sebanyak 20000 bilangan.

set.seed(1)

# Membangkitkan 1000 bilangan acak Binom(size=8, p=0.25)
binom.rand <- rbinom(20000, size = 8, prob = 0.25)

# Untuk membandingkannya kita akan buat tabulasi dari binom.rand
tab <- table(binom.rand)

# Menghitung frekuensi relatif (peluang empiris)
rasio <- tab/sum(tab)

# Menghitung peluang teoritis binomial(size = 8, p = 0.25)
# kemungkinan nilai x : 0 - 8
x <- 0:8

prob.x <- dbinom(x, size = 8, prob = 0.25)

# Membandingkan hasil
banding <- rbind(empiris = rasio, teoritis = prob.x)
colnames(banding) <- x

# Membulatkan dalam 5 digit desimal
round(banding, 5)

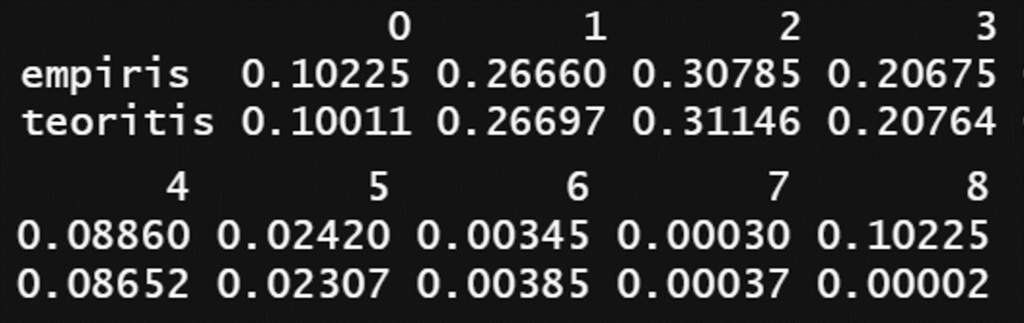
Hasil tabulasi menunjukkan nilai sebaran peluang dari bilangan acak bagi setiap kemungkinan nilai x dari 0 – 8 (empiris). Hasil ini mendekati dengan peluang teoritis sebaran $Binomial(n = 8, p = 0.25)$ (dalam contoh ini, yang agak berbeda pada x=8).

Pada prinsipnya karena proses ini adalah proses acak maka banyak kemungkinan yang dapat terjadi. Jika menggunakan seed yang berbeda atau tanpa seed atau dengan jumlah sampel berbeda tentu saja hasilnya juga berbeda. Namun secara umum akan menghasikan sebaran yang sesuai.

Silahkan mencoba pembangkitan bilangan acak dari sebaran lainnya menggunakan fungsi yang bersesuaian r{nama_sebaran} (misal rnorm, rgamma, rbeta, dsb) serta menyesuaikan nilai-nilai parameternya.

Fungsi built-in pada R tentu hanya menyediakan pembangkitan bilangan acak untuk sebaran-sebaran yang sudah umum. Adapun untuk sebaran lainnya yang tidak tersedia, kita dapat menggunakan metode lain salah satunya adalah inverse-transform.

Metode Inverse-Transform didasarkan pada teori Probalility Integral Transformation yaitu jika $X$ adalah peubah acak kontinu dengan fungsi peluang kumulatif (cdf) $F(X)$, maka $U = F(X) \sim Seragam(0, 1)$

Berdasarkan teori tersebut maka:

$F^{-1}(u) = inf\{x : F(x) = u\}$, dimana $0 < u < 1$

Selanjutnya, jika $U \sim Seragam(0, 1)$, maka untuk setiap $x$ anggota $R$ berlaku

$$\begin{aligned}P(F^{-1}_X (u) \leq x) &= P(inf \{t : F_X(t) = U\} \leq x) \\&= P(U \leq F_X(x)) \\&= F_U(F_X(x)) \\&= F_X(x)\end{aligned}$$

dari persamaan ini berarti $F^{-1}_X(u)$ mempunyai sebaran yang sama dengan $X$

Secara umum langkah-langkah untuk membangkitkan bilangan acak $X$ dengan metode inverse-transform adalah sebagai berikut:

1. Bangkitkan bilangan acak $u$ (misal sebanyak n bilangan) dari sebaran $Seragam(0, 1)$
2. Gunakan fungsi kumulatif peluang (cdf) dari sebaran $X$ untuk setiap bilangan acak $u$ sehingga mendapatkan $x \sim ~ F^{-1}(u)$
3. Berdasarkan teorema sebelumnya $F^{-1}(u)$ memiliki sebaran yang sama dengan $X$ sehingga hasil dari perhitungan pada point ke-2 akan memiliki sebaran sesuai yang diinginkan.

Contoh penerapan metode inverse-transform yang akan dibahas terdiri dari dua bagian yaitu untuk sebaran kontinu dan diskret.

Bangkitkan 1000 data dari $X \sim f(x) = 4x^3$ untuk $0 < x < 1$!

Berdasarkan fungsi tersebut kita perlu mencari terlebih dahulu cdf dari $f(x)$, yaitu $F_X(x)$.

$$F_X(x) = \int{4x^3}dx = x^4$$ (abaikan konstanta C-nya)

Selanjutnya cari fungsi invers dari $F_X(x)$, yaitu $F^{-1}(u)$

$$F^{-1}(u) = u^{1/4}$$

dengan batas fungsi $u$ adalah $0 < u < 1$

# membangkitkan 1000 bilangan  u dari sebaran uniform(0, 1)
# versi lengkap : u = runif(1000, min = 0, max = 1)
u = runif(1000)

# hitung nilai x berdasarkan invers fungsi kumulatif
x <- u^(1/4)

# Melihat sebaran dari data x
hist(x, prob = T)

# Membuat kurva sebaran teoritis fx = 4x^3 0 < x < 1
x.axis <- seq(0, 1, 0.01)
y.axis <- 4*x.axis^3

lines(x.axis, y.axis, col="red", lwd=1.5)

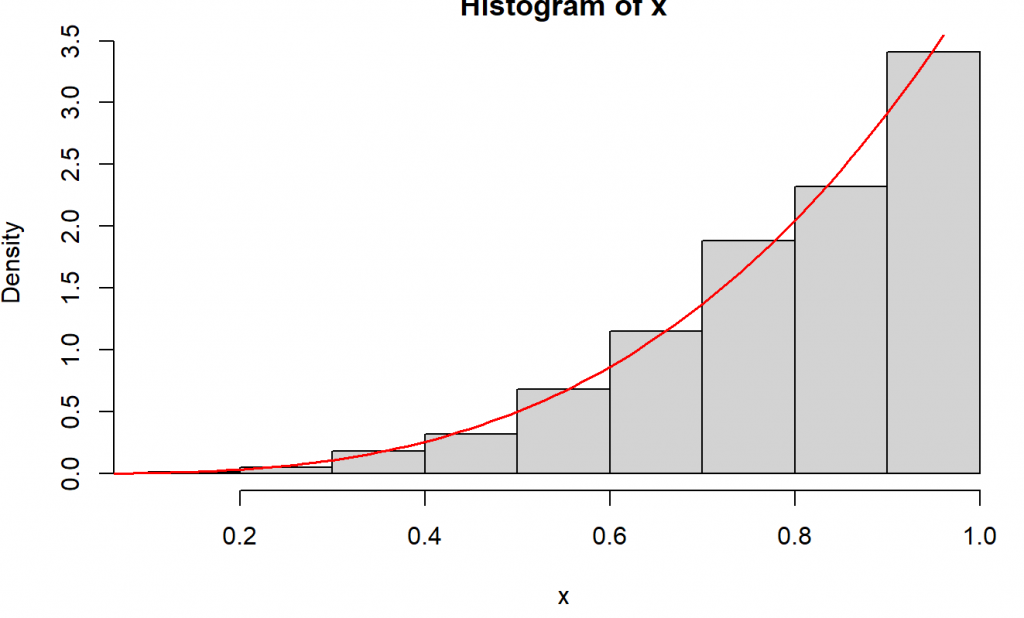
Seperti penjelasan pada subbagian sebelumnya, output pembangkitan 1000 bilangan acak berdasarkan bentuk histogramnya tampak mengikuti kurva dari fungsi sebaran $f(x) = 4x^3$ untuk $0 < x < 1$.

Misalkan $X$ adalah peubah acak jumlah angka dari kejadian pelemparan 2 dadu. Bangkitkanlah 1000 bilangan dari sebaran peubah acak tersebut?

Untuk menyelesaikan soal tersebut langkah pertama menentukan fungsi peubah acak $X$ dan fungsi kumulatifnya

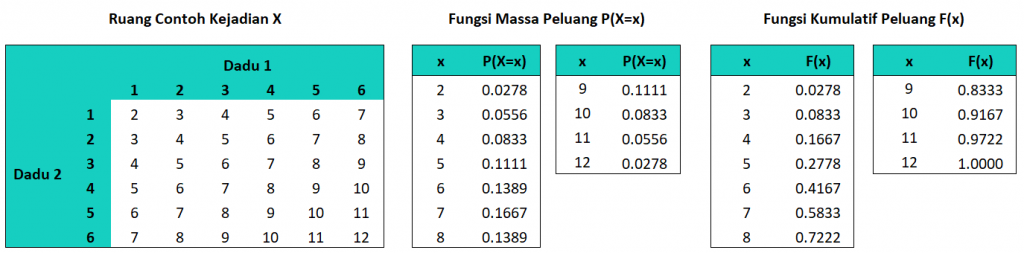
Selanjutnya kita dapat menggunakan informasi tersebut untuk membuat fungsi invers dari $F(x)$ menggunakan bahasa R. Pada contoh ini untuk menghitung $P(X=x)$ dan $F(x)$ akan kita buat fungsi tersendiri. (Namun jika ingin lebih sederhana, dapat menyimpan nilai-nilai seperti pada gambar dalam vektor untuk digunakan langsung)

# Bagian 1 :

# Ruang contoh untuk peubah acak x
# Membuat kemungkinan kombinasi penjumlahan dua dadu bermata 6
s <- outer(1:6, 1:6, FUN = "+")

# Tabulasi frekuensi untuk setiap nilai x
x <- table(s)

# Menghitung peluang setiap peubah acak x 
px <- x/length(s)

# Menghitung peluang kumulatif
# nilai peubah acak x dimulai dari angka 2, px[1] = 2
# untuk mengakses elemen vektor px kita kurangi dulu x dengan 1
indeks <- x-1
pk <- sapply(2:12, function(x) sum(px[1:indeks]))

# Fungsi invers peluang kumulatif
fun.pk.inv <- function(p) {
  for(i in 2:12) {
    if(p <= pk[i-1]) return (i) 
  }
}

# Bagian 2 :

set.seed(1)

# Membangkitkan 10000 bilangan Uniform(0, 1)
u <- runif(10000)

# bilangan acak yang menyebar F-invers (x)
rand <- sapply(u, fun.pk.inv)

# Visualisasi

# Menghitung frekueansi relatif dari data rand
p.empiris <- table(rand)/length(rand)

# Membuat barplot dari data yang dibangkitkan
barplot(table(rand), col="orange", space = 1)

# Membandingkan peluang empiris dan toeritisnya
# Dibulatkan 4 angka desimal
round(rbind(px, p.empiris), 4)

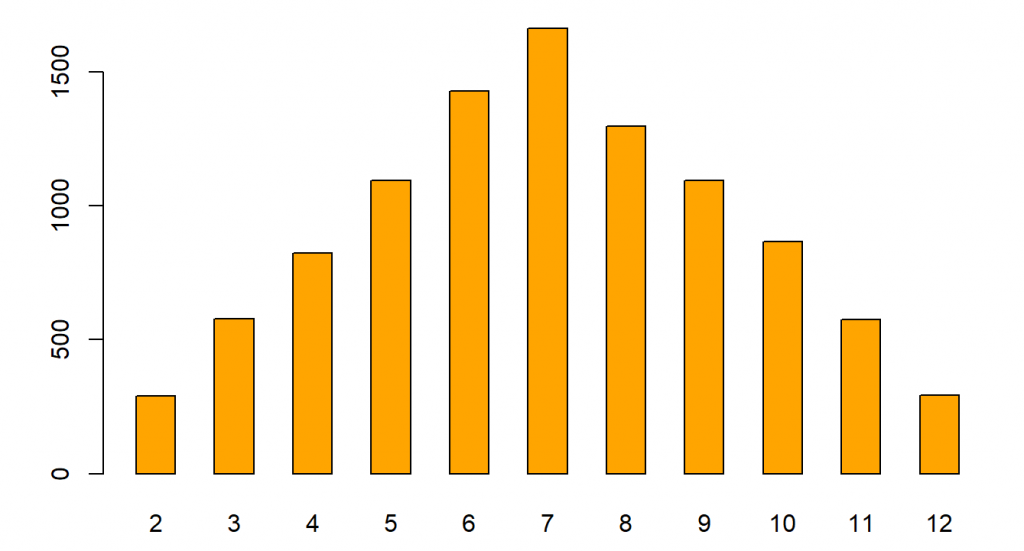
Langkah pembangkitan bilangan acak ditunjukkan pada bagian 2. Prosesnya dimulai dengan membangkitkan sejumlah bilangan acak $u$ yang menyebar $Seragam(0, 1)$. Selanjutnya untuk setiap nilai $u$ kita hitung nilai dari $F^{-1}(u)$ dan disimpan dalam variabel rand. Berdasarkan teori yang sudah dibahas, maka sebaran dari rand akan mengikuti sebaran dari pmf-nya.

Selanjutnya, kita dapat membuat barplot untuk menggambarkan sebaran data. Kita juga membandingkan frekuensi relatifnya (peluang empiris) dengan FMP teoritisnya. Dari hasil tersebut antara peluang empiris dan pmf-nya memiliki nilai yang mirip, sehingga dapat kita yakini bahwa bilangan acak tersebut sudah mengikuti sebaran yang diharapkan.

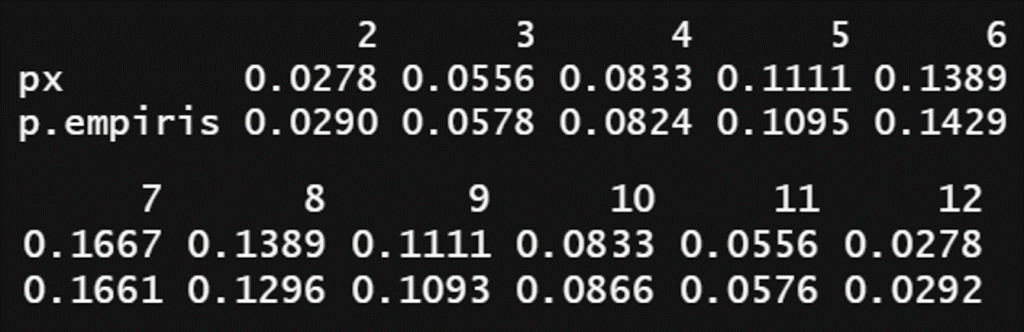
Pembangkitan bilangan acak menggunakan metode inverse-transform umumnya cukup mudah dilakukan selama fungsi invers-nya bisa diperoleh. Namun permasalahan yang mungkin muncul adalah tidak semua fungsi kumulatif peluang memiliki fungsi invers-nya, atau jikapun ada mungkin tidak dalam bentuk closed-form sehingga sulit menerapkan metode ini pada kondisi tersebut.

Metode ini tidak mensyaratkan invers dari fungsi kumulatif. Inti dari metode ini adalah memanfaatkan sebaran tertentu (yang sudah diketahui, disebut sebaran proposal). Sebaran proposal dapat berupa sebaran apapun dengan batas-batas sama dengan sebaran target yang diinginkan.

Langkah-langkah pada metode acceptance-rejection yaitu:

1. Misalkan $X$ dan $Y$ adalah dua buah peubah acak dengan fungsi peluang masing-masing $f$ dan $g$ serta batas kedua fungsi adalah sama, dimana terdapat konstanta $c$ sedemikian sehingga $f(t)/g(t) \leq c$ untuk semua $t : f(t) > 0$. ($X$ adalah peubah acak dari sebaran yang kita inginkan, dan $Y$ adalah peubah acak dari sebaran proposal)
2. Cari nilai konstanta $c$ yang memenuhi $f(t)/g(t) \leq c$ untuk semua $t : f(t) > 0$
3. Bangkitkan sebuah bilangan acak $u$ yang menyebar $Seragam(0, 1)$
4. Bangkitkan sebuah bilangan acak $y$ yang menyebar $g$ (sebaran proposal)
5. Hitung nilai $c \cdot g(y) \cdot u$, jika $c \cdot g(y) \cdot u \leq f(y)$, maka terima y sebagai x (kita terima sebagai angka acak)
6. Jika tidak terpenuhi maka kita tolak dan ulangi langkah 3 hingga langkah 5 terpenuhi.

Bangkitkan 1000 angka acak yang mengikuti sebaran sebaran $Beta(\alpha=2, \beta=5)$ !

Kita tahu bahwa tersedia fungsi builtin untuk sebaran $Beta$ namun kita akan melakukannya secara manual menggunakan metode acceptance-rejection.

Pertama kita tentukan fungsi sebaran yang diinginkan yaitu:

$$f(x, \alpha = 2, \beta = 5) = \frac{\Gamma_{2 + 5}}{\Gamma_{2}\Gamma_{5}}x^{2-1}(1 – x)^{5-1}$$

Selanjutnya tetapkan sebaran proposal yang memiliki batas yang sama dengan $f(x)$ yaitu $0 < x < 1$. Dalam hal ini yang paling sederhana untuk digunakan adalah sebaran $Seragam(0, 1)$.

Kemudian cari nilai konstanta $c$ yang merupakan nilai maksimum dari $f(t)/g(t)$, dan lakukan pengecekan nilai $c \cdot g(y) \cdot u < f(y)$

# Membuat fkp fungsi Beta(alpha, beta)
dist.beta <- function(x, alpha, beta) {
  return(gamma(alpha+beta)/(gamma(alpha)*gamma(beta))*x^(alpha-1)*(1-x)^(beta-1))
}

# Sebaran proposal yang kita gunakan adalah Uniform(0, 1)
# di R fungsi pdf-nya adalah dunif(x, min = 0, max = 1)
# pdf Uniform(0, 1) = 1, 
# Namun agar ilustrasi lebih general
# contoh ini menggunakan dunif(x, min, max)  : nilainya 1

# Mencari nilai maximum dari (f/g) pada batas-batas fungsi
c <- optimise(function(t) dist.beta(t, 2, 5)/dunif(t, 0, 1), 
              interval = c(0, 1), maximum = TRUE)$objective


# dapat dilakukan pembulatan ke atas
c <- ceiling(c)

set.seed(1)

n = 1000
iter <- idx <- 0
y = numeric(n)

# iterasi hingga memperoleh 1000 angka acak
while(idx < n){
  iter = iter+1
  # bangkitkan 1 angka acak Seragam(0, 1)
  u <- runif(1) 

  # bangkitkan 1 angka acak sebaran proposal 
  #(dalam contoh ini adalah Uniform(0,1))
  x <- runif(1) 

  # tambahkan x jika fx(x) > c*g(x)*u
  # jika tidak, lanjutkan iterasi
  if(dist.beta(x) > c*dunif(x, 0, 1)*u) {
    idx <- idx+1
    y[idx] <- x
  }
}

# Membuat histogram data hasil pembangkitan
hist(y, prob = T, breaks = 15)

# membuat kurva sebaran Beta(alpha=2, beta=5)
x.axis <- seq(0, 1, .01)
lines(x.axis, sapply(x.axis, dist.beta), col="red", lwd=1.5)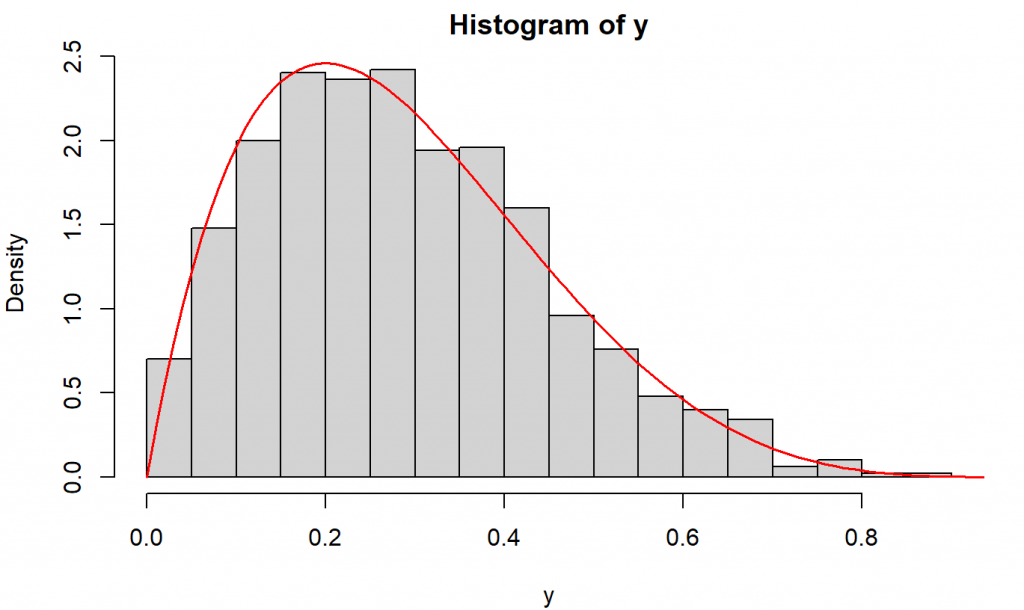

Dari gambar tersebut bentuk histogram dari bilangan acak yang dihasilkan sesuai dengan kurva sebaran teoritisnya yaitu $Beta(\alpha=2, \beta=5)$.

Untuk menggunakan metode ini kita perlu memahami bentuk-bentuk transformasi suatu peubah acak. Contoh kali ini, kita akan membangkitkan bilangan acak yang menyebar $Fisher(df1, df2)$ dengan cara melakukan transformasi dari dua sebaran $\chi^2$ yang saling bebas. (Pada R kita bisa membangkitkan secara langsung angka acak untuk sebaran $Fisher$ menggunakan fungsi rf(n, df1, df2), namun kita tidak menggunakan fungsi ini untuk menunjukkan pembangkitan melalui transformasi peubah acak sebaran lainnya)

$$F(df_1, df_2) = \frac{\chi^2_{df_1}/df_1}{\chi^2_{df_2}/df_2}$$

Jadi, yang akan kita lakukan untuk contoh ini adalah membangkitkan bilangan acak yang menyebar $\chi^2_{df_1}$ dan $\chi^2_{df_2}$, selanjutnya dari bilangan acak tersebut kita akan melakukan transformasi sehingga memperoleh bilangan acak yang mengikuti sebaran $F(df_1, df_2)$.

set.seed(9)

# Membangkitkan bilangan acak dari sebaran chi-kuadrat dengan df = 9
chi1 <- rchisq(1000, df = 9)
# Membangkitkan bilangan acak dari sebaran chi-kuadrat dengan df = 15
chi2 <- rchisq(1000, df = 15)

# Melakukan transformasi untuk memperoleh sebaran F
f <- (chi1/9)/(chi2/15)

# Membuat histogram dari data yang dibangkitkan
hist(f, prob = T, breaks = 20, ylim=c(0, 0.8))
# Membuat kurva sebaran F(df1=9, df2=15) pada selang 0 - 8
x.axis <- seq(0, 7, .01)
lines(x.axis, sapply(x.axis, df, df1=9, df2=15), col="red", lwd=1.5)

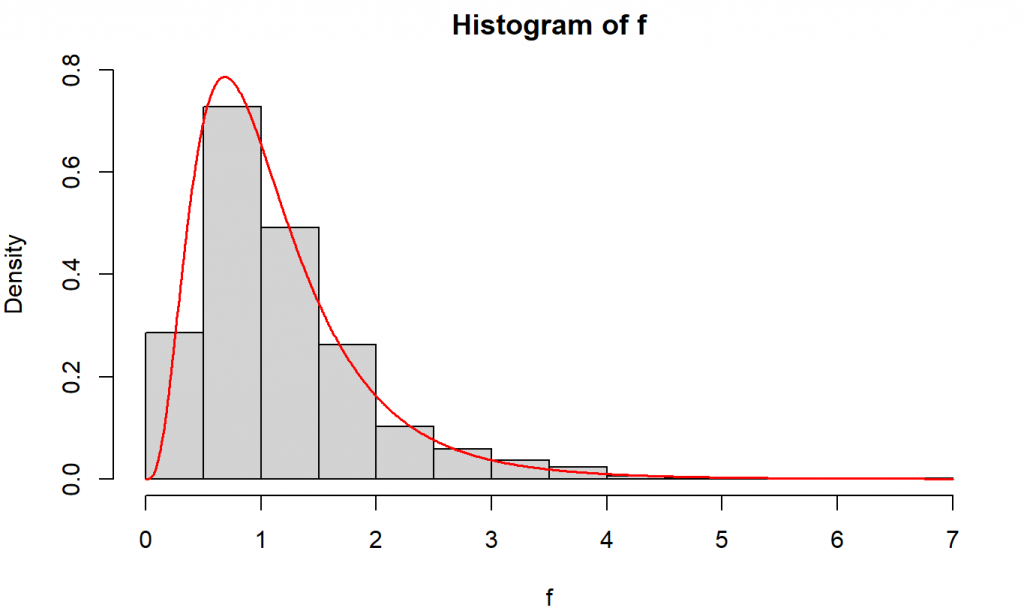
Histogram dan kurva tersebut menunjukkan bahwa bilangan acak yang dihasilkan dimana awalnya berasal dari dua sebaran $\chi^2$, namun setelah dilakukan transformasi akan mengikuti kurva sebaran $F$ yang kita harapkan.

• Bahasa R menyediakan berbagai fungsi builtin yang berkaitan dengan fungsi dari beberapa sebaran populer. Fungsi ini juga mencakup fungsi untuk membangkitkan bilangan acaknya (fungsi r...())
• Jika fungsi yang diinginkan belum tersedia, pembangkitan dapat dilakukan menggunakan metode inverse-transform, metode acceptance-rejection ataupun transformasi peubah acak
• Dari beberapa contoh yang sudah disampaikan, dapat diyakini bahwa sebaran angka acak yang dibangkitkan benar-benar mengikuti sebaran yang diharapkan
• Angka acak yang sudah dihasilkan selanjutnya dapat digunakan untuk keperluan lebih lanjut sesuai kepentingan peneliti

• Soleh, M. Agus. STA561 Pemrograman Statistika: Pembangkitan Bilangan Acak

Tulisan lainnya :

• Sebaran Peubah Acak Diskret
• Python : Membangkitkan Data Simulasi untuk Model Regresi dengan Numpy
• Membangkitkan Bilangan Acak untuk Sebaran Tertentu dengan Python Numpy