Membangkitkan Bilangan Acak Berbagai Sebaran dengan Numpy


Pembangkitan bilangan acak merupakan prosedur yang sering digunakan dalam bidang Statistika. Prosedur ini biasanya dilakukan untuk menghasilkan sejumlah angka acak yang mengikuti distribusi peluang tertentu. Hasil pembangkitan ini dapat digunakan sebagai data simulasi untuk model-model statistik tertentu sebelum penerapannya pada data real.
Pada tulisan ini kita akan membahas beberapa metode dalam pembangkitan bilangan acak menggunakan library numpy dengan bahasa pemrograman python. Terdapat 3 teknik yang akan kita bahas yaitu:
- Fungsi Built-In pada Numpy
- Metode Inverse-Transform
- Metode Acceptance-Rejection
Adapun penjelasan teoritis pada metode-metode tersebut (khususnya metode ke-2 dan ke-3) dapat dilihat pada tulisan dengan topik yang sama namun untuk bahasa pemrograman R.
Lihat : Pembangkitan Bilangan Acak pada Bahasa R
Fungsi Built-In Numpy
Library numpy menyediakan berbagai fungsi untuk membangkitkan bilangan acak yang mengikuti sebaran tertentu. Beberapa di antaranya adalah uniform, normal, beta, binomial, geometric, gamma dan sebagainya. Sesuai dengan namanya, masing-masing fungsi tersebut berguna untuk membangkitkan bilangan acak yang menyebar uniform, normal dan seterusnya.
Setiap fungsi memiliki parameter yang berbeda-beda tergantung parameter sebarannya. Misalkan fungsi normal memiliki 2 parameter utama yaitu loc yang menunjukkan nilai tengah ($\mu$) serta scale yang menunjukkan standar deviasi ($\sigma$). Contoh lainnya pada fungsi binomial, terdapat 2 parameter yaitu n dan p. Dimana n menunjukkan jumlah ulangan pada kejadian binomial, serta p adalah nilai peluang suksesnya untuk setiap ulangan.
Parameter lainnya yang ada di setiap fungsi adalah size. Parameter ini menentukan banyaknya bilangan acak yang akan dibangkitkan sesuai sebaran fungsinya.
Fungsi-fungsi tersebut dapat diakses melalui objek kelas np.random.default_rng. Kelas ini memiliki parameter seed agar bilangan acak yang dibangkitkan dapat di-reproduce. Pada fungsi yang sama misal normal(loc=10, scale=4, size=10), dengan nilai seed yang sama maka 10 bilangan acak yang dibangkitkan selalu sama walaupun dijalankan berulang kali bahkan pada perangkat yang berbeda.
Pada bagian ini, kita akan membuat contoh pembangkitan untuk tiga sebaran yaitu Normal, Gamma dan Binomial. Silahkan mengksplorasi untuk sebaran lainnya.
Adapun pustaka yang akan digunakan adalah sebagai berikut:
Python
import pandas as pd import numpy as np import scipy as sc import seaborn as sns import matplotlib.pyplot as plt
Contoh 1. Sebaran Normal
Contoh pertama kita akan membangkitkan 1000 bilangan acak yang menyebar Normal dengan nilai tengah ($\mu=50$) dan standar deviasi ($\sigma=5$) atau varians ($\sigma^2=25$).
Python
# membuat objek Random Generator rng = np.random.default_rng(100) # membangkitkan 1000 bilangan acak yang menyebar Normal(50, 5) rand_normal = rng.normal(loc=50, scale=5, size=1000) print(rand_normal)
Output
# output [44.21225176 51.44877901 53.90427035 52.71986822 45.19308679 55.35504333 53.5072783 53.52486728 53.72531301 55.52173619 61.21486198 46.94253439 50.23605592 58.77117341 43.31010067 51.62787234 46.55441142 49.90089095 ... 48.92494872 60.43292257 47.13352136 51.62641108 46.45120237 53.84437706 46.68522611 58.03537651 47.3638051 49.59084702 49.75388741 51.68737455 46.96721373 41.18927933 40.70986609 48.84285343]
Dari hasil kode di atas, diperoleh 1000 bilangan acak yang menyebar Normal($\mu=50$, $\sigma=5$). Untuk melihat apakah data yang dibangkitkan benar-benar mengikuti sebaran tersebut, kita dapat membuat histogram dari data. Kemudian membandingkan pola yang terbentuk dengan kurva fungsi sebaran Normal($\mu=50$, $\sigma=5$) yang sebenarnya.
Untuk visualisasi, kita akan menggunakan library seaborn (dan matplotlib).
Python
plt.figure(figsize=(8, 4))
sns.set_style("ticks")
# Histogram dari bilangan acak yang dibangkitkan
sns.histplot(data=rand_normal, stat="density", color="grey", alpha=0.6)
# Membuat kurva sebaran teoritis dari normal(50, 5)
# Pada kisaran nilai X 30 hingga 70
x = np.linspace(30, 70, 1000)
y = sc.stats.norm.pdf(x, loc=50, scale=5)
sns.lineplot(x=x, y=y, color="red")
plt.show()Output


Histogram dari bilangan acak yang dibangkitkan jika dibandingkan dengan kurva sebaran Normal($\mu=50$, $\sigma=5$) sudah mengikuti pola yang sama. Hasil ini menunjukkan bahwa bilangan acak yang dibangkitkan sesuai dengan sebaran yang diharapkan.
Contoh 2. Sebaran Gamma
Pada contoh berikut, kita akan membangkitkan bilangan acak yang mengikuti sebaran Gamma($\alpha=2$, $\beta=3$). Pada fungsi gamma nilai $\alpha$ ditentukan menggunakan parameter shape dan untuk $\beta$ menggunakan parameter scale.
Python
# membuat objek Random Generator rng = np.random.default_rng(100) # membangkitkan 1000 bilangan acak yang menyebar Gamma(alpha=2, beta=3) rand_gamma = rng.gamma(shape=2, scale=3, size=1000) print(rand_gamma)
Output
# Output [10.58859504 7.07613542 5.05958664 7.43920833 12.92861652 1.44814649 0.30015268 4.9182727 12.42640173 8.21690514 1.24936408 5.9356957 14.60836712 1.15309587 11.50150046 5.60319566 6.20088785 4.09600228 ... 15.30161843 1.13925879 1.32710586 2.57260665 14.58175341 6.32008475 6.64517793 0.43559 4.00160495 8.4146116 1.70915956 3.67988137 14.42713457 3.28289779 12.64419744 4.85826988]
Dengan cara yang sama kita juga dapat membuat visualisasi sebaran data yang sudah dihasilkan seperti berikut ini:
Python
plt.figure(figsize=(8, 4))
sns.set_style("ticks")
# Histogram dari bilangan acak yang dibangkitkan
sns.histplot(data=rand_gamma, stat="density", color="grey", alpha=0.6)
# Membuat kurva sebaran teoritis dari Gamma(alpha=2, beta=3)
x = np.linspace(0, 25, 1000)
# pada scipy, gamma.pdf nilai alpha = a
y = sc.stats.gamma.pdf(x, a=2, scale=3)
sns.lineplot(x=x, y=y, color="red")
plt.show()Output
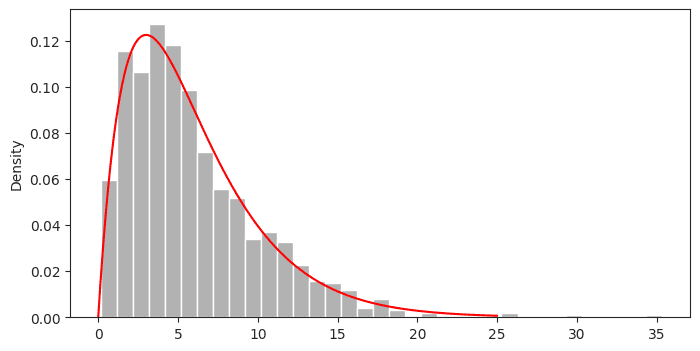

Histogram di atas juga menunjukkan bahwa data yang dibangkitkan mengikuti sebaran Gamma($\alpha=2$, $\beta=3$) sesuai yang telah ditentukan.
Contoh 3. Sebaran Binomial
Dua contoh sebelumnya, kita membangkitkan bilangan acak dari sebaran kontinu. Sekarang, kita akan membangkitkan bilangan acak yang mengikuti sebaran diskret yaitu binomial. Pada contoh ini, jumlah ulangan dari percobaan binomial kita tentukan sebanyak n=10 dengan peluang sukses pada setiap ulangan sebesar p=0,7 atau Binomial($n=10$, $p=0.7$).
Python
# membuat objek Random Generator rng = np.random.default_rng(100) # membangkitkan 1000 bilangan acak yang menyebar Binom(n=5, p=0.7) rand_binom = rng.binomial(n=10, p=0.7, size=1000) print(rand_binom)
Output
# Output [ 8 8 8 7 7 8 10 9 4 6 5 8 7 7 7 8 8 4 8 5 9 6 6 7 9 6 6 9 8 7 4 7 5 7 7 5 6 9 8 7 6 10 6 5 9 8 7 9 4 9 9 7 6 5 7 7 6 7 3 6 7 6 7 5 9 6 7 8 3 5 6 7 ... 6 7 7 7 7 8 9 7 8 8 4 8 7 9 8 8 7 6 5 4 6 8 9 5 8 5 9 8 6 6 7 5 7 8 6 8 8 7 8 8 7 7 5 5 7 7 8 7 8 3 8 6 8 6 8 9 8 7 6 4 7 5 9 6]
Pada pembangkitan bilangan acak yang menyebar Binomial($n=10$, $p=0.7$) nilai yang dihasilkan terdiri dari 11 kemungkinan yaitu antara 0 sampai 10. Nilai ini menunjukkan banyaknya sukses yang terjadi dari 10 kali percobaan dimana peluang sukses untuk setiap percobaan adalah 0,7.
Python
plt.figure(figsize=(6, 4))
sns.set_style("ticks")
# Histogram dari bilangan acak yang dibangkitkan
sns.histplot(data=rand_binom, stat="percent", color="grey", discrete=True, shrink=0.8)
plt.show()Output
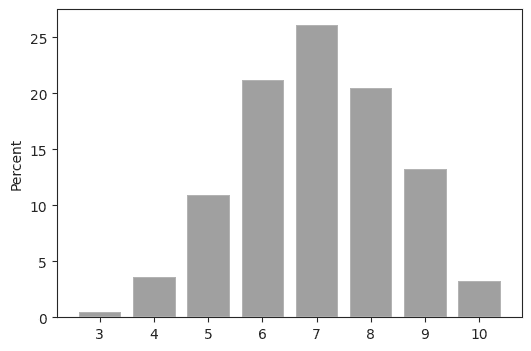

Untuk melihat hasil dari bilangan yang dibangkitkan adalah dengan menghitung proporsi sukses dan membandingkan dengan nilai peluang sebaran binomial yang sesuai.
Python
X = range(0, 11)
# Menghitung frekuensi menurut jumlah sukses dari 1000 bilangan
y = np.array([np.count_nonzero(rand_binom == x) for x in X])
# menghitung proporsi menurut frekuensi jumlah sukses
proporsi = y/1000
# menghitung peluang P(X=x) pada sebaran binom(n=10, p=0.7)
peluang = np.array([sc.stats.binom.pmf(x, n=10, p=0.7) for x in X])
# Menyajikan perbandingan dalam bentuk dataframe
pd.DataFrame({"X": X),
"Proporsi": np.round(proporsi, 3),
"P(X=x)": np.round(peluang, 3)}).TOutput


Baris X pada output di atas menunjukkan banyaknya sukses dari 10 kali ulangan kejadian binomial. Dimana kemungkinan nilainya adalah dari 0, 1, 2 hingga 10 kali.
Nilai proporsi menunjukkan frekuensi relatif atau banyaknya jumlah sukses untuk nilai X tertentu dari 1000 bilangan acak yang dibangkitkan dibagi dengan 1000. Pada contoh di atas, dari 1000 bilangan acak, angka 5 muncul sebanyak 100 kali atau 10%.
Nilai P(X=x) menunjukkan nilai peluang untuk x tertentu pada sebaran Binomial($n=10$, $p=0.7$).
Melihat dari perbandingan antara proporsi setiap nilai X dengan nilai peluang teoritisnya yang relatif mirip, menunjukkan bahwa bilangan acak yang dibangkitkan sudah mengikuti sebaran yang sesuai.
Metode Inverse-Transform
Fungsi pembangkitan bilangan acak pada numpy dapat digunakan untuk berbagai sebaran yang sudah umum dikenal. Namun tidak semua sebaran tersedia fungsinya pada numpy. Oleh karena itu perlu metode tertentu agar dapat membangkitkan bilangan acak yang mengikuti sebaran tersebut. Salah satu metode yang digunakan adalah metode invers-transform.
Secara umum langkah-langkah metode Inverse-Transform untuk membangkitkan bilangan acak $X$ yang mengikuti sebaran tertentu adalah sebagai berikut:
- Bangkitkan bilangan acak $u$ (sebanyak n bilangan) dari sebaran Uniform(0, 1)
- Gunakan fungsi kumulatif peluang (cdf) dari sebaran $X$ untuk setiap bilangan acak $u$ sehingga mendapatkan $x \sim ~ F^{-1}(u)$
- Hasil dari $F^{-1}(u)$ memiliki sebaran yang sama dengan $X$ sehingga hasil dari perhitungan pada point ke-2 akan memiliki sebaran sesuai yang diinginkan.
Sesuai namanya, metode ini mensyaratkan fungsi peluang kumulatifnya harus memiliki invers.
Pada bagian ini, kita akan membuat 1 contoh untuk sebaran kontinu dan 1 contoh untuk sebaran diskret.
Contoh untuk Sebaran Kontinu
Misalkan kita akan membangkitkan 1000 bilangan acak yang menyebar $X \sim f(x) = 4x^3$ untuk $0 < x < 1$.
Langkah-langkah yang perlu dilakukan adalah seperti berikut ini:
Bangkitkan 1000 bilangan acak yang menyebar Uniform(0, 1)
kedua, berdasarkan fungsi tersebut kita perlu mencari fungsi kumulatif peluang (cdf) dari $f(x)$, yaitu $F_X(x)$.
$$F_X(x) = \int{4x^3}dx = x^4$$ (abaikan konstanta C-nya)
Ketiga, cari fungsi invers dari $F_X(x)$, yaitu $F^{-1}(u)$
$$F^{-1}(u) = u^{1/4}$$
dengan batas fungsi $u$ adalah $0 < u < 1$
Python
# membuat objek Random Generator rng = np.random.default_rng(100) # membangkitkan bilangan acak menyebar uniform(0, 1) rand_u = rng.uniform(low=0, high=1, size=1000) # menghitung invers cdf-nya untuk setiap nilai rand_u rand_data = rand_u ** (1/4) # rand_data akan menyebar mengikuti fungsi sebaran 3x^4 (0 < rand_data < 1) print(rand_data)
Output
# Output [0.78456155 0.85383936 0.8752719 0.89442263 0.91412274 0.90073116 0.85713195 0.98573271 0.93907855 0.83953081 0.75735258 0.68314614 0.67066107 0.94316907 0.75133058 0.67319359 0.59190276 0.99092719 ... 0.73757113 0.83077052 0.75144996 0.83002551 0.75053429 0.85913695 0.99684964 0.9959626 0.89817169 0.94276577 0.78728648 0.82309693 0.99728616 0.96704964 0.96249956 0.79157588]
Seperti sebelumnya, kita dapat membuat histogram dari data yang dibangkitkan dan membandingkan dengan kurva sebaran $4x^3$.
Python
plt.figure(figsize=(8, 4))
sns.set_style("ticks")
# Histogram dari bilangan acak yang dibangkitkan
sns.histplot(data=rand_data, stat="density", color="grey", alpha=0.6)
# Membuat kurva sebaran teoritis dari f(x) = 4x^3
x = np.linspace(0, 1, 1000)
y = 4 * x**3
sns.lineplot(x=x, y=y, color="red")
plt.show()Output
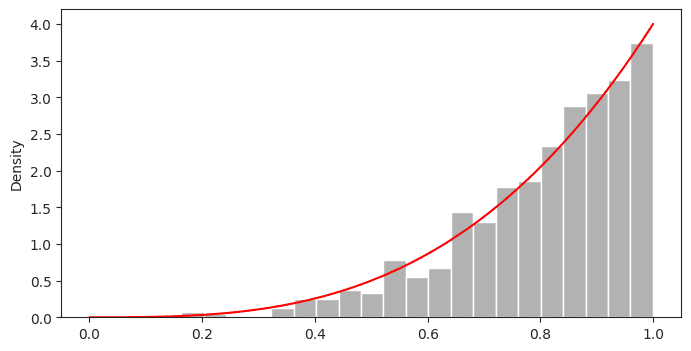

Contoh untuk Sebaran Diskret
Misalkan kita akan membangkitkan 1000 bilangan acak dari sebaran penjumlahan mata dadu pada pelemparan 2 dadu. Ilustrasi dari sebaran ini ditunjukkan pada gambar berikut:
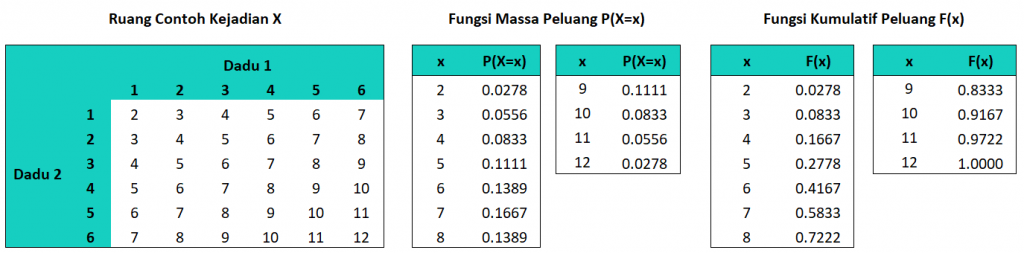

Distribusi nilai yang memungkinkan untuk kejadian ini adalah 2 hinga 12, kejadian 2 yaitu ketika mata dadu pertama bernilai 1 dan mata dadu kedua bernilai 1. Dari gambar, nilai X dengan peluang tertinggi adalah untuk x=7 yaitu sebesar 0,1667. Nilai ini dapat dicapai dengan 6 kemungkinan kondisi yaitu {(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)}.
Seperti contoh sebelumnya, kita perlu membuat fungsi peluang kumulatifnya serta mencari fungsi inversnya. Pertama kita perlu membuat fungsi massa peluang dari sebaran ini. Namun, karena banyaknya nilai x tidak terlalu besar, maka kita akan menggunakan nilai yang sudah tertera seperti pada gambar.
Python
list_X = range(2, 13)
peluang_X = np.array([0.0278, 0.0556, 0.0833, 0.1111, 0.1389, 0.1667,
0.1389, 0.1111, 0.0833, 0.0556, 0.0278])
# membuat fungsi massa peluang P(X=x)
def pmf_dadu(x):
if x>=2 and x<=12:
indeks = x-2 # indeks array peluang_x dimulai dari 0
return peluang_X(indeks)
else:
return 0
# membuat fungsi kumulatif peluang F(X=x)
# P(x=2) + P(x=3) + ... + P(x=x)
def cdf_dadu(x):
if x<2:
return 0
if x>=2 and x<=12:
indeks = x-2
return peluang_X[:indeks+1].sum()
else:
return 1
# Membuat fungsi inverse kumulatif F^-1(X=x)
# mengembalikan nilai x dimana cdf(x) >= peluang
def cdf_inv_dadu(peluang):
for x in list_X:
cdf_x = cdf_dadu(x)
if cdf_x >= peluang:
return xFungsi pmf kita buat secara manual berdasarkan data pada gambar, namun kita perlu menambah 2 fungsi lagi untuk menghitung peluang kumulatif dan menghitung inversnya.
Setelah memiliki fungsi invers dari peluang kumulatif, maka langkah selanjutnya sama dengan sebelumnya pada contoh sebaran kontinu.
Python
# membuat objek Random Generator rng = np.random.default_rng(100) # membangkitkan bilangan acak menyebar uniform(0, 1) rand_u = rng.uniform(low=0, high=1, size=1000) # menghitung invers cdf-nya untuk setiap nilai rand_u rand_data = np.array([cdf_inv_dadu(u) for u in rand_u]) # rand_data akan menyebar mengikuti fungsi sebaran yang sesuai print(rand_data)
Output
# Output [ 7 6 7 10 2 4 8 9 4 7 10 5 5 4 5 12 9 5 9 5 7 11 9 6 5 6 2 5 9 2 8 8 4 6 3 10 12 3 10 7 9 8 7 2 5 7 9 5 6 10 12 10 6 8 6 6 5 5 3 7 6 8 8 4 11 11 8 6 6 5 5 5 ... 9 3 8 8 3 7 12 3 7 3 6 8 4 7 11 8 8 10 11 4 5 4 10 9 12 9 4 11 2 7 9 10 6 8 4 8 5 7 11 3 5 7 4 11 8 7 9 8 9 6 5 2 4 5 8 11 10 11 6 8 6 4 3 8]
Dengan cara di atas, kita sudah mendapatkan 1000 bilangan acak yang mengikuti sebaran jumlah mata dadu dari pelemparan dua dadu. Selanjutnya kita dapat membuat visualisasi dan membandingkan dengan nilai sebaran teoritisnya.
Python
plt.figure(figsize=(6, 4))
sns.set_style("ticks")
# Histogram dari bilangan acak yang dibangkitkan
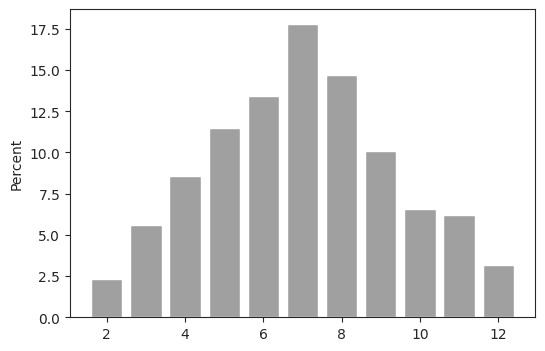
sns.histplot(data=rand_data, stat="percent", color="grey", discrete=True, shrink=0.8)
plt.show()Output

Python
# Menghitung frekuensi menurut nilai mata dadu dari 1000 bilangan
y = np.array([np.count_nonzero(rand_data == x) for x in list_X])
# menghitung proporsi menurut frekuensi setiap nilai mata dadu
proporsi = y/1000
# Menyajikan perbandingan dalam bentuk dataframe
pd.DataFrame({"X": X,
"Proporsi": np.round(proporsi, 3),
"P(X=x)": np.round(peluang_X, 3)}).TOutput


Hasil di atas menunjukkan proporsi dari 1000 bilangan acak yang diperoleh, baik untuk x=2 hingga x=12, memiliki nilai yang cukup mirip dengan nilai peluang teoritis untuk masing-masing nilai x. Sehingga dapat dikatakan bahwa bilangan acak tersebut memiliki sebaran sesuai dengan yang diharapkan.
Metode Acceptance-Rejection
Metode ini tidak memerlukan penghitungan invers dari fungsi sebaran yang akan dibangkitkan. Inti dari metode acceptance-rejection adalah memanfaatkan sebaran tertentu (yang sudah diketahui) yang disebut sebaran proposal. Sebaran proposal dapat berupa sebaran apapun asalkan memiliki batas-batas sama dengan sebaran target yang kita inginkan.
Langkah-langkah pada metode acceptance-rejection yaitu:
- Misalkan $X$ dan $Y$ adalah dua buah peubah acak dengan fungsi peluang masing-masing $f$ dan $g$ serta batas kedua fungsi adalah sama, dimana terdapat konstanta $c$ sedemikian sehingga $f(t)/g(t) \leq c$ untuk semua $t : f(t) > 0$. ($X$ adalah peubah acak dari sebaran yang kita inginkan, dan $Y$ adalah peubah acak dari sebaran proposal)
- Cari nilai konstanta $c$ yang memenuhi $f(t)/g(t) \leq c$ untuk semua $t : f(t) > 0$
- Bangkitkan sebuah bilangan acak $u$ yang menyebar $Seragam(0, 1)$
- Bangkitkan sebuah bilangan acak $y$ yang menyebar $g$ (sebaran proposal)
- Hitung nilai $c \cdot g(y) \cdot u$, jika $c \cdot g(y) \cdot u \leq f(y)$, maka terima y sebagai x (kita terima sebagai angka acak)
- Jika tidak terpenuhi maka kita tolak dan ulangi langkah 3 hingga langkah 5 terpenuhi.
Untuk contoh metode ini kita akan membangkitkan 1000 bilangan acak yang mengikuti sebaran $Beta(\alpha=2, \beta=5)$.
Seperti diketahui, kita dapat menggunakan fungsi built-in pada numpy menggunakan fungsi beta. Namun untuk contoh ini, anggap saja fungsi tidak tersedia dan kita akan melakukannya dengan metode accpetance-rejection.
Sebaran Beta memiliki bentuk sebagai berikut:
$$f(x, \alpha = 2, \beta = 5) = \frac{\Gamma_{2 + 5}}{\Gamma_{2}\Gamma_{5}}x^{2-1}(1 – x)^{5-1}$$
Selanjutnya tentukan sebaran proposal yang memiliki batas yang sama dengan $f(x)$ yaitu $0 < x < 1$. Dalam hal ini yang paling sederhana tentunya adalah sebaran Uniform(0, 1).
Kemudian cari nilai konstanta $c$ yang merupakan nilai maksimum dari $f(t)/g(t)$, dan lakukan pengecekan nilai $c \cdot g(y) \cdot u < f(y)$
Python
# Import Fungsi gamma dari scipy
# (bukan sebaran gamma)
from scipy.special import gamma
# FKP Sebaran Beta
def pdf_beta(x, alpha, beta):
return (gamma(alpha+beta) / (gamma(alpha) * gamma(beta)) * x**(alpha-1) * (1-x)**(beta-1))
# Kita gunakan sebaran proposal uniform(0, 1)
# nilai uniform(0, 1) sebenarnya = 1
# untuk generalisasi, maka dibuat fungsi sendiri
def pdf_proposal(x, bb, ba):
return sc.stats.uniform.pdf(x, bb, ba)
# Fungsi perbandingan kita negatifkan (-)
# Dengan alasan pencarian menggunakan fungsi minimize
def beta_per_prop(x):
return -pdf_beta(x, alpha=2, beta=5)/pdf_proposal(x, bb=0, ba=1)Python
# Import Fungsi minimize dari scipy from scipy.optimize import minimize # Mencari f(x) minimum min = minimize(beta_per_prop, 0.5, method='BFGS') # Nilai minimum fungsi kita kali (-1) # Agar kembali menjadi nilai fungsi aslinya c = min.fun * -1 print(c) # Output # 2.457599999999998
Python
# membuat objek Random Generator
rng = np.random.default_rng(100)
n = 1000
rand_data = []
while len(rand_data) < n:
# membangkitkan 2 angka acak menyebar uniform(0,1) untuk u dan x
u = rng.uniform(low=0, high=1) # atau rs.uniform()
x = rng.uniform()
# Jika kondisi terpenuhi, tambahkan x sebagai bilangan acak terpilih
# jika tidak maka bangkitkan ulangi prosesnya
if pdf_beta(x, 2, 5) > c * u * pdf_proposal(x, 0, 1):
rand_data.append(x)
# Menyimpan dalam format numpy array
rand_data = np.array(rand_data)
print(rand_data)Output
# Output [0.04295157 0.18999147 0.32192526 0.1316484 0.08240137 0.52412082 0.22724696 0.38472241 0.14887393 0.184949 0.10685547 0.07369337 0.22351108 0.39434801 0.19179735 0.31065823 0.27069433 0.40063662 ... 0.17210224 0.14253558 0.48659636 0.18951127 0.37716141 0.27374589 0.29443886 0.20583149 0.28813939 0.20587598 0.24572419 0.09674313 0.06549807 0.23204672 0.71165082 0.14191493]
Python
plt.figure(figsize=(8, 4))
sns.set_style("ticks")
# Histogram dari bilangan acak yang dibangkitkan
sns.histplot(data=rand_data, stat="density", color="grey", alpha=0.6)
# Membuat kurva sebaran beta(alpha=2, beta=5)
x = np.linspace(0, 1, 1000)
y = pdf_beta(x, alpha=2, beta=5)
sns.lineplot(x=x, y=y, color="red")
plt.show()Output
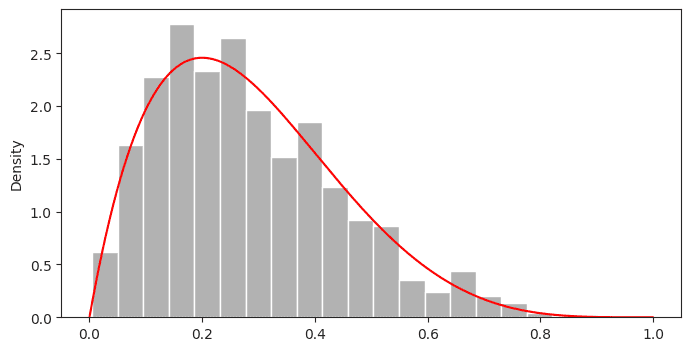

Perbandingan histogram dengan kurva sebaran $Beta(\alpha=2, \beta=5)$ menunjukkan bilangan acak yang dibangkitkan sudah mengikuti sebaran sesuai yang ditentukan.
Referensi
- Soleh, M. Agus. STA561 Pemrograman Statistika: Pembangkitan Bilangan Acak
- Numpy Random Generator Documentation : random-generator








