Hierarchical Clustering: Agglomerative Cluster dengan Python

Hierarchical Clustering (Pengklasteran Berhirarki) adalah metode pengelompokan objek berdasarkan kesamaan antar objek tersebut. Pada hierarchical clustering tidak mensyaratkan jumlah cluster yang harus ditentukan sebelum pengelompokan. Jumlah cluster terpilih dapat ditentukan kemudian sesuai ukuran yang diinginkan. Hasil dari pengelompokan adalah representasi berbasis pohon dari objek-objek tersebut, yang juga dikenal sebagai dendrogram. Dendrogram adalah hierarki multilevel di mana cluster pada satu tingkat digabungkan untuk membentuk cluster pada tingkat berikutnya. Hal ini memungkinkan kita untuk menentukan pada tingkat mana pohon akan dipotong untuk menghasilkan kelompok objek data yang sesuai.

Secara umum hierarchical clustering dapat dibagi menjadi dua jenis:

• Agglomerative Clustering, di mana setiap individu pengamatan awalnya akan dianggap sebagai cluster tersendiri (leaves). Kemudian, cluster yang paling mirip digabungkan secara bertahap hingga hanya ada satu cluster besar (root).
• Divisive Clustering, berkebalikan dari aglomerative clustering, pada divisive clustering, semua objek tergabung ke dalam satu cluster besar. Kemudian cluster yang paling heterogen dipisahkan secara bertahap hingga semua objek berada dalam cluster mereka sendiri.

Agglomerative clustering adalah jenis hierarchical clustering yang paling umum digunakan untuk mengelompokkan objek berdasarkan kesamaannya. Metode ini juga dikenal sebagai AGNES (Agglomerative Nesting). Algoritma aglomerative clustering bekerja dengan cara “bottom-up”. Artinya, setiap objek awalnya dianggap sebagai cluster dengan anggota satu elemen (leaves). Pada setiap langkah algoritma, dua cluster yang paling mirip digabungkan menjadi cluster baru yang lebih besar (node). Prosedur ini diulang hingga semua titik menjadi anggota dari satu cluster besar (root).

Divisive Clustering atau DIANA (divisive analysis), adalah jenis hierarchical clustering di mana proses dimulai dengan memasukkan seluruh objek sebagai satu cluster tunggal dan kemudian secara bertahap dibagi menjadi cluster yang lebih kecil. Prosesnya terbalik dari agglomerative clustering. Keuntungan dari pendekatan divisive yaitu dapat menghasilkan cluster yang lebih spesifik dan terpisah secara alami. Namun, ini juga dapat menjadi lebih kompleks serta membutuhkan waktu komputasi yang lebih lama dibandingkan metode agglomerative, terutama untuk dataset besar.

Pada tutorial ini, kita akan fokus pada metode pengelompokan objek menggunakan agglomerative clustering. Sementara untuk divisive clustering akan dibahas pada tutorial selanjutnya.

Untuk memutuskan objek/cluster mana yang harus digabungkan,diperlukan metode untuk mengukur kemiripan antara objek. Pengukuran ini digunakan untuk menentukan jarak antara objek-objek, yang merupakan langkah sangat penting dalam aglomerative clustering.

Beberapa metrik jarak yang umum digunakan untuk mengukur kemiripan antara objek-objek meliputi:

Jarak Euclid mengukur jarak langsung antara dua titik dalam ruang berdimensi $n$. Ini adalah metode yang paling umum digunakan dalam clustering. Formula untuk memperoleh jarak euclid adalah:

$$d(\mathbf{p}, \mathbf{q}) = \sqrt{\sum_{i=1}^{n} (q_i – p_i)^2}$$. Di mana, $\mathbf{p}$ dan $\mathbf{q}$ adalah vektor yang mewakili dua objek, dan $p_i$​ dan $q_i$​ adalah nilai-nilai variabel untuk setiap dimensi.

Jarak Manhattan adalah jumlah absolut perbedaan antara koordinat titik-titik dalam ruang berdimensi $n$. Rumusnya adalah: $$d(\mathbf{p}, \mathbf{q}) = \sum_{i=1}^{n} |q_i – p_i|$$

Jarak Minkowski adalah bentuk generalisasi dari jarak Euclidean dan Manhattan, didefinisikan sebagai:

$$d(\mathbf{p}, \mathbf{q}) = \left( \sum_{i=1}^{n} |q_i – p_i|^r \right)^{\frac{1}{r}}$$

​Di mana, $r$ adalah parameter yang mengontrol jenis jarak. Ketika $r = 2$, maka menjadi jarak Euclidean, dan ketika $r = 1$, menjadi jarak Manhattan.

Jarak Mahalanobis mengukur jarak antara dua titik dalam ruang berdimensi $n$ dengan mempertimbangkan kovarians data. Oleh akrena itu, jarak Mahalanobis robust terhadap perbedaan satuan data tanpa harus melakukan standardisasi data terlebih dahulu. Namun, normalisasi ataupun standardisasi data sebelum masuk ke dalam penghitungan merupakan praktik yang tetap dianjurkan.

$$d(\mathbf{p}, \mathbf{q}) = \sqrt{(\mathbf{p} – \mathbf{q})^T \mathbf{S}^{-1} (\mathbf{p} – \mathbf{q})}$$​ Di mana, $\mathbf{S}$ adalah matriks kovarians dari data.

Korelasi Pearson digunakan untuk mengukur tingkat korelasi antara dua variabel. Ini memberikan informasi tentang arah dan kekuatan hubungan antara dua variabel. Nilai korelasi berkisar dari -1 hingga 1, di mana nilai 1 menunjukkan korelasi positif sempurna, nilai -1 menunjukkan korelasi negatif sempurna, dan nilai 0 menunjukkan tidak ada korelasi.

Jarak kosinus mengukur sudut antara dua vektor dalam ruang berdimensi $n$. jarak ini sering digunakan untuk data berbasis teks atau data yang berorientasi pada kata. Jarak kosinus antara dua vektor $\mathbf{p}$ dan $\mathbf{q}$ didefinisikan sebagai: $$\text{cos}(\mathbf{p}, \mathbf{q}) = \frac{\mathbf{p} \cdot \mathbf{q}}{\|\mathbf{p}\| \cdot \|\mathbf{q}\|}$$

​Di mana, $\mathbf{p} \cdot \mathbf{q}$ adalah hasil perkalian titik antara dua vektor, dan $\|\mathbf{p}\|$ dan $\|\mathbf{q}\|$ adalah panjang vektor $\mathbf{p}$ dan $\mathbf{q}$, masing-masing.

Pemilihan metode tergantung pada jenis data yang kita miliki dan apa yang ingin dicapai dari analisis yang dilakukan. Misalnya, jika memiliki data numerik, maka metode Euclidean atau Manhattan mungkin cocok. Sedangkan jika data berbasis teks, metode cosine similarity mungkin lebih relevan.

Linkage merujuk pada metode atau kriteria yang digunakan untuk mengukur jarak atau kesamaan antara dua cluster ketika mereka digabungkan. Kriteria ini menentukan bagaimana jarak antara cluster dihitung pada setiap langkah pengelompokan. Terdapat beberapa kriteria linkage yang dapat digunakan meliputi single linkage, complate linkage, average linkage, centroid linkage dan metode ward.

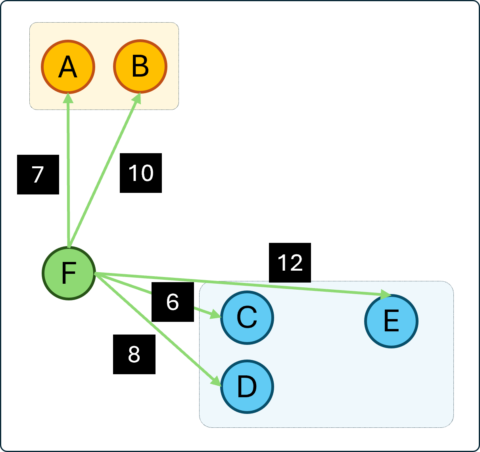
Untuk memperjelas pemahaman masing-masing linkage, telah disajikan ilustrasi proses agglomerative clustering pada Gambar 1. Katakanlah saat ini, dari 6 objek sudah terkelompokkan menjadi 3 cluster dengan cluster 1 beranggotakan A dan B, cluster 2 beranggotakan C, D dan E, serta cluster ketiga dengan 1 anggota yaitu F. Tahapan selanjutnya pada agglomerative yaitu mengelompokkan 3 cluster menjadi 2. Dalam hal ini misalkan F akan dikelompokkan ke dalam cluster 1 atau 2.

Perbedaan linkage yang digunakan dapat menghasilkan perbedaan cluster yang terbentuk. Pada masing-masing rincian di bawah ini, akan diilustrasikan bagaimana pengukuran yang dilakukan serta cluster baru yang terbentuk hasil penggabungan tersebut.

Pada complete linkage atau dikenal juga dengan “further neighbors”, jarak antara dua cluster didefinisikan sebagai jarak maksimum dari semua elemen dalam suatu cluster dengan elemen-elemen dalam cluster lainnya. Metode ini cenderung menghasilkan cluster yang lebih kompak.

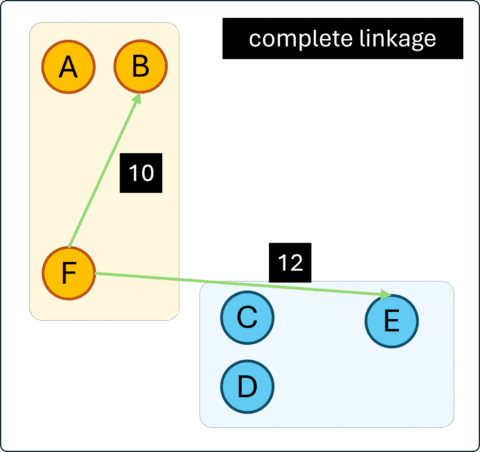
Berdasarkan contoh Gambar 2, maka jarak maksimum antara cluster ke-3 (F) dengan cluster ke-1 adalah 10, yaitu jarak dengan objek B. Adapun jarak terjauh cluster ke-3 dengan cluster ke-2 adalah 12, yaitu dengan objek E. Karena jarak F ke objek terjauh pada cluster 2, lebih pendek dibandingkan ke cluster 3, maka pada tahapan ini, F akan dikelompokkan ke dalam cluster 1 bersama A dan B.

Berkebalikan dengan complete linkage, jarak antara dua cluster pada single linkage atau “nearest neighbors” didefinisikan sebagai nilai minimum dari semua jarak antara elemen-elemen pada suatu cluster dengan elemen-elemen cluster lainnya. Metode ini cenderung menghasilkan kluster yang panjang dan “longgar”.

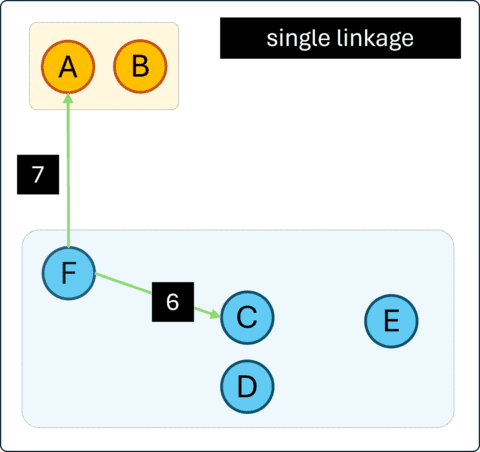
Pada contoh ini, cluster ke-3 (F) memiliki jarak terdekat ke cluster 1 sebesar 7, sementara jarak terdekat ke cluster 2 adalah 6. Sehingga, F akan digabungkan dengan cluster ke-2 bersama C, D dan E.

Jarak antara dua cluster didefinisikan sebagai rata-rata jarak antara elemen dalam sebuah kluster dengan elemen dalam cluster lainnya.

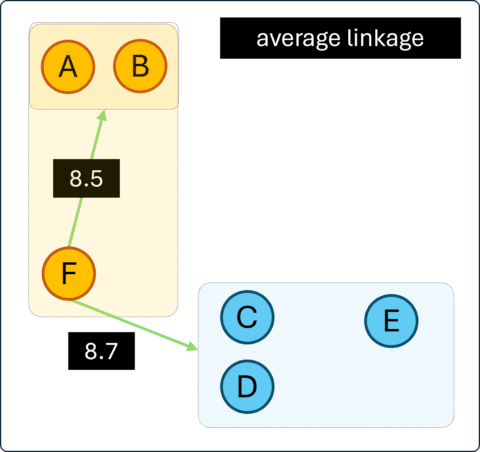
Jika menggunakan average linkage maka berdasarkan Gambar 4, cluster ke-3 (F) akan digabungkan bersama cluster ke-1 dengan A dan B. Di mana, jarak F ke cluster 1 adalah $\frac{1}{2} \dot (7+10)=8.5$, dan jarak ke cluster 2 adalah $\frac{1}{3}\dot (6+8+12)=8.7$.

Centroid linkage mengukur jarak antara dua kluster didefinisikan sebagai jarak antara centroid untuk suatu cluster (vektor rata-rata dari p variabel) dan centroid untuk cluster lainnya. Penentuan lokasi centroid tentunya memerlukan nilai setiap variabel pada semua anggota cluster.

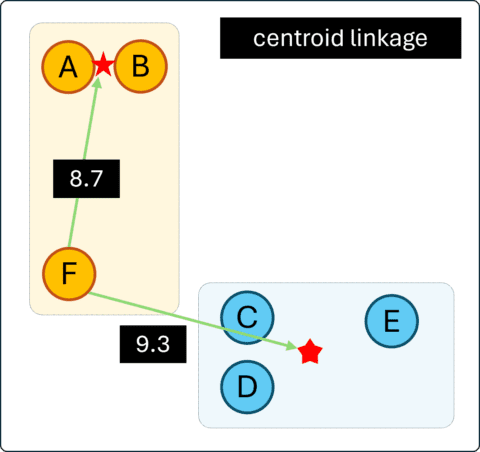
Sama seperti sebelumnya, cluster ke-3 (F) akan digabungkan menurut jarak terdekat antara centroid cluster ke-3 dengan cluster lainnya. Pada Gambar 5, dimisalkan jarak terdekat adalah terhadap centroid cluster 1 yaitu 8,7. Berdasarkan hasil ini, maka F akan digabungkan ke Cluster 1.

Metode ward bertujuan meminimalkan peningkatan varians dalam cluster setelah dilakukan penggabungan. Pada setiap langkah, pasangan cluster dengan jarak antar kluster minimum akan digabungkan. Ukuran peningkatan total varians ketika dua cluster digabungkan diperoleh sebagai jumlah kuadrat jarak antara setiap objek dalam cluster dengan centroid cluster tersebut. Perhitungant ersebut dapat ditulis dengan persamaan berikut:

$$\text{Varians } C_k = \sum_{i \in C_k} d(i, c_k)^2$$

dimana,$d(i, c_k)$ adalah jarak antara objek $i$ dan centroid cluster $C_k$​.

Bedasarkan hasil penghitungan varians tersebut, maka penggabungan cluster terpilih yaitu yang menghasilkan peningkatan varians terkecil.

Selain beberapa metode yang sudah disampaikan, terdapat bebeberapa pilihan lain seperti median linkage, mcquitty dan sebagainya.

Tersedia beberapa paket untuk membuat agglomerative clustering. Paket pertama tentunya scikit-learn yang memang merupakan paket utama dalam python unutk machine learning termasuk clustering. Paket kedua dan yang akan kita gunakan pada tutorial ini adalah scipy melalui modul scipy.cluster.hierarchy. Untuk analisis hierarchical clustering, scipy mungkin sedikit unggul karena juga menyediakan secara langsung pembuatan dendogram sebagai alat visualisasi.

Data yang akan digunakan adalah data Indikator ekonomi dan sosial 34 Provinsi di Indonesia Tahun 2021. Secara ringkas dataset berisi beberapa informasi mengenai indikator dari 34 Provinsi di Indonesia tahun 2021. Keterangan masing-masing variabel juga dapat dilihat pada output kode di bawah ini.

import pandas as pd

data = pd.read_csv("Data 34 Provinsi 2021.csv")

print(data.info())

# menjadikan nama provinsi sebagai indeks baris
data.index = data["Provinsi"]
data.drop("Provinsi", axis=1, inplace=True)

# menampilkan beberapa ringkasan statistik
print(data.describe().transpose()[["mean", "min", "max", "std"]])

# OUTPUT

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 34 entries, 0 to 33
Data columns (total 12 columns):
 #   Column          Non-Null Count  Dtype  
---  ------          --------------  -----  
 0   Provinsi        34 non-null     object       # Nama Provinsi
 1   PDRB_KAPITA     34 non-null     int64        # PDRB per Kapita (Ribu Rupiah)
 2   IPM             34 non-null     float64      # Indeks Pembangunan Manusia (%)
 3   TPT             34 non-null     float64      # Tingkat Pengangguran Terbuka (%)
 4   PST_KEMISKINAN  34 non-null     float64      # Persentase Penduduk Miskin (%)
 5   AHH_L           34 non-null     float64      # Angka Harapan Hidup Laki-laki (Tahun)
 6   AHH_P           34 non-null     float64      # Angka Harapan Hidup Perempuan (Tahun)
 7   APS_07_12       34 non-null     float64      # Angka Partisipasi Sekolah Usia 7-12 (%)
 8   APS_13_15       34 non-null     float64      # Angka Partisipasi Sekolah Usia 13-15 (%)
 9   APS_16_18       34 non-null     float64      # Angka Partisipasi Sekolah Usia 16-18 (%)
 10  APS_19_23       34 non-null     float64      # Angka Partisipasi Sekolah Usia 19-23 (%)
 11  PST_PEROKOK     34 non-null     float64      # Persentase Perokok (%)
dtypes: float64(10), int64(1), object(1)
memory usage: 3.3+ KB
None

# Ringkasan Statistik
                        mean       min        max           std
PDRB_KAPITA     67053.176471  20555.00  274660.00  51796.120975
IPM                71.361176     60.62      81.11      3.937439
TPT                 5.492059      3.01       9.91      1.818745
PST_KEMISKINAN     10.762353      4.53      26.86      5.402680
AHH_L              70.550588     65.78      73.27      1.830632
AHH_P              74.890000     69.76      78.12      2.110548
APS_07_12          98.825294     83.43      99.76      2.759620
APS_13_15          95.552059     80.02      99.43      3.497575
APS_16_18          75.218235     63.98      89.63      6.000716
APS_19_23          29.739412     19.10      56.41      7.024927
PST_PEROKOK        28.004706     19.58      34.07      3.063703

Jika diperlukan, dapat dilakukan analisis data eksploratif terlebih dahulu dari data tersebut. Namun, pada tutorial ini kita akan langsung ke topik yag menjadi bahasan utama yaitu membuat hieralchical clustering menggunakan metode agglomerative.

Modul scipy.cluster.hierarchy menyediakan fungsi linkage yang digunakan untuk membuat hierarchical clustering khususnya agglomerative. Fungsi linkage memiliki 4 parameter yaitu:

• y: dataset yang akan dilakukan clustering
• method: metode linkage digunakan ("single", "complete", "average", "weighted", "centroid", "median", dan "ward")
• metric: metrik jarak yang digunakan terdapat 23 metrik yang dapat digunakan, beberapa diantaranya adalah "euclidean", "minkowski", "cityblock", "seuclidean", "sqeuclidean", "cosine", "correlation", "hamming" dan sebagainya. (lihat selengkapnya pada tautan di bagian akhir tulisan). Kita juga bisa menambahkan fungsi sendiri, jika metrik yang ingin digunakan belum tersedia.
• optimal_ordering: boolean. Jika bernilai True maka matriks linkage akan diurutkan ulang sehingga jarak antara daun-daun berurutan minimal. Hal ini menghasilkan struktur pohon yang lebih intuitif ketika data divisualisasikan. Default-nya adalah False, karena algoritma ini dapat menjadi lambat, terutama pada data yang besar.

Fungsi linkage mengembalikan output berupa matriks jarak yang dikondensasi, Y. Untuk setiap $i$ dan $j$ (dimana $i < j$), dimana $m$ adalah jumlah observasi asli. Metrik $dist(u=X[i], v=X[j])$ dihitung dan disimpan pada entri $m \times i + j – \frac{{(i + 2) \times (i + 1)}}{2}$. Namun di sini kita tidak akan membahas detail isian output tersebut, karena nantinya akan kita tampilkan ke dalam bentuk dendogram.

Silahkan mengeksplorasi berbagai metode linkage maupun metrik untuk digunakan. Pada kode berikut akan disajikan 2 contoh saja sebagai ilustrasi.

from sklearn.preprocessing import StandardScaler
from scipy.cluster.hierarchy import linkage

# standardisasi nilai setiap kolom
scaler = StandardScaler()
X_scaled = scaler.fit_transform(data)

# Membuat hierarchical cluster
clust_ward_euclid = linkage(X_scaled, method="ward", metric="euclidean")
clust_comp_mahal = linkage(X_scaled, method="complete", metric="mahalanobis")

print(f"Cluster dengan Metode Ward dan Jarak Euclid:\n {clust_ward_euclid}\n")
print(f"Cluster dengan Metode Complete dan Jarak Mahalanobis:\n {clust_comp_mahal}\n")

# OUTPUT

Cluster dengan Metode Ward dan Jarak Euclid:
 [[11.         15.          0.89259226   2.        ]
  [12.         14.          0.940213     2.        ]
  [ 3.         23.          1.01463148   2.        ]
  [ 8.         20.          1.24875031   2.        ]
     .         ..                  ...  ..
  [61.         63.         10.41106632  21.        ]
  [33.         62.         12.07352276  13.        ]
  [64.         65.         13.55448652  34.        ]]

Cluster dengan Metode Complete dan Jarak Mahalanobis:
 [[ 0.          1.          1.82295687   2.        ]
  [ 4.         27.          1.96917692   2.        ]
  [ 8.         24.          1.98065826   2.        ]
  [11.         15.          2.03778839   2.        ]
     .         ..                  ...   .. 
  [10.         63.          6.89055126   3.        ]
  [62.         64.          7.00257953  33.        ]
  [33.         65.          7.54122805  34.        ]]

Hasil cluster yang diperoleh melalui fungsi linkage dapat kita visualisasikan menggunakan fungsi dendogram. Fungsi ini tersedia pada modul scipy.cluster.hierarchy. Terdapat cukup banyak parameter yang dapat diatur untuk menghasilkan dendogram yang diinginkan. Beberapa diantaranya adalah sebagai berikut:

• Z: Matriks linkage (output dari fungsi linkage).
• p: Mengatur kedalaman pohon (jika dilakukan pemangkasan pada truncate_mode)
• truncate_mode: dendrogram akan sulit dibaca ketika matriks data asli besar. Pemangkasan digunakan untuk memotong dendrogram. Ada beberapa mode yang dapat digunakan:
  • None: Tidak ada pemangkasan yang dilakukan (default).
  • 'lastp': Cluster terakhir p bukan singleton yang terbentuk dalam penggabungan menjadi satu-satunya simpul bukan daun dalam pengelompokan. Semua cluster bukan singleton lainnya ditetapkan menjadi simpul daun.
  • 'level‘: Tidak lebih dari p level pohon dendrogram ditampilkan. ‘"‘level' mencakup semua simpul dengan p penggabungan dari penggabungan terakhir.
• color_threshold: mengatur batas warna pada dendogram berdasarkan jarak. (Misalkan 5, berarti setiap node dan jalur akan diberikan warna berbeda menurut pengelompokan sampai batas jarak 5).
• orientation: mengatur posisi dendogram. Secara default bernilai 'top' yaitu node root berada di bagian atas dan node leaves di bawah. Namun dapat diatur menjadi 'bottom', 'left', atau 'right'.
• labels: Secara default, label adalah None. Namun dapat diatur dengan daftar label untuk ditampilkan. Misalkan dalam contoh sebelumnya yaitu nama-nama provinsi yang bersesuaian.
• dsb (lihat selengkapnya pada tautan di bagian akhir tulisan)

Sebagian besar parameter tersebut bersifat opsional kecuali Z. Jadi jika tidak ditentukan akan diatur mengikuti nilai default-nya.

Python

from scipy.cluster.hierarchy import dendrogram
import matplotlib.pyplot as plt

# Menggunakan hasil Ward dan jarak Euclid
plt.figure(figsize=(12, 7))
dendrogram(
    clust_ward_euclid,
    orientation="top",
    color_threshold=8,
    labels=data.index,
    distance_sort="descending",
    show_leaf_counts=True,
)

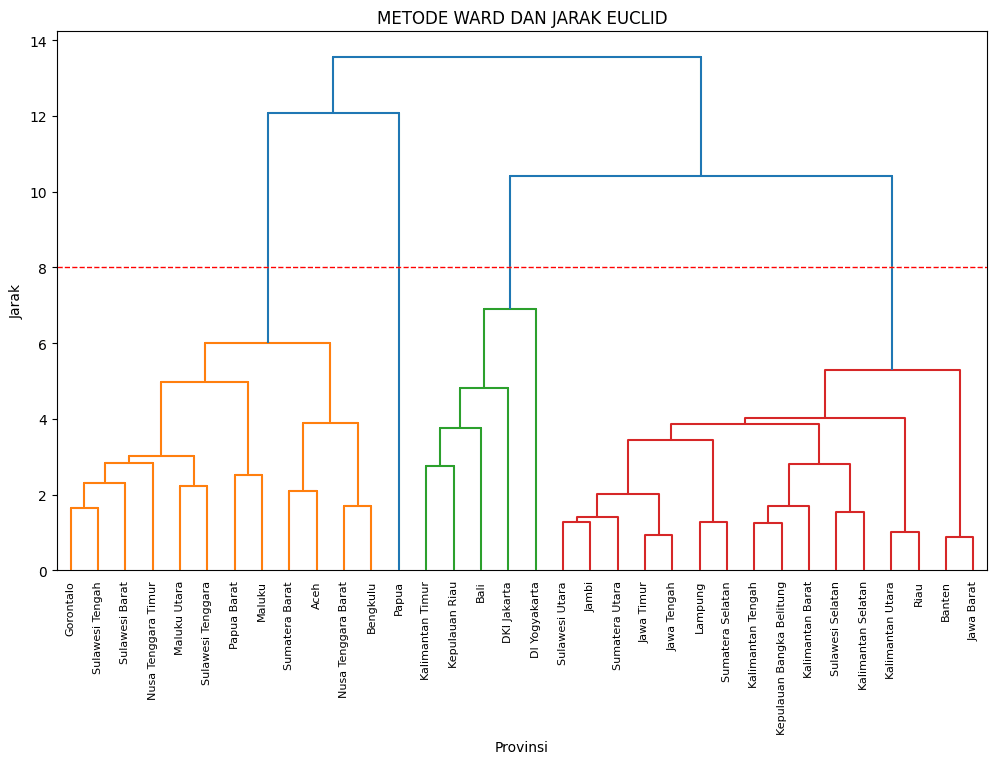
plt.title("METODE WARD DAN JARAK EUCLID")
plt.xlabel("Provinsi")
plt.ylabel("Jarak")

# Menambah garis merah putus-putus pada jarak 8
plt.axhline(y=8, color="r", linestyle="--", linewidth=1)
# Menjadikan tulisan pada sumbu x menjadi vertikal
plt.xticks(rotation=90)
plt.show()


# Menggunakan hasil Complete dan jarak Mahalanobis
plt.figure(figsize=(10, 7))
dendrogram(
    clust_comp_mahal,
    orientation="right",
    color_threshold=5.5,
    labels=data.index,
    distance_sort="descending",
    show_leaf_counts=True,
)

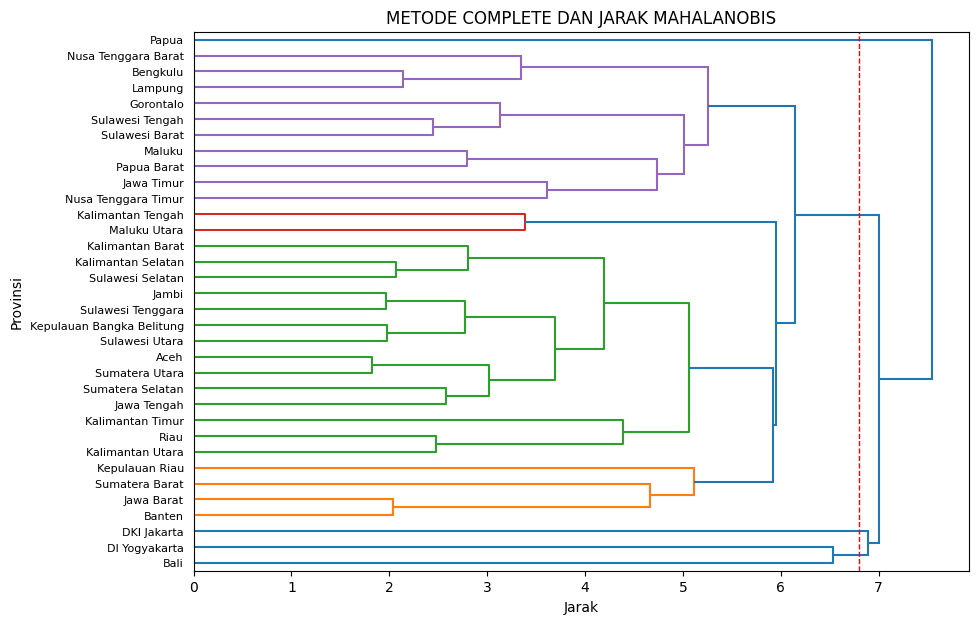
plt.title("METODE COMPLETE DAN JARAK MAHALANOBIS")
plt.xlabel("Jarak")
plt.ylabel("Provinsi")

# Menambah garis merah putus-putus pada jarak 6.8
plt.axvline(x=6.8, color="r", linestyle="--", linewidth=1)
plt.show()


# Menggunakan hasil Complete dan jarak Mahalanobis (truncated)
plt.figure(figsize=(10, 7))
dendrogram(
    clust_comp_mahal,
    orientation="right",
    p=4,
    truncate_mode="level",  # dipangkas menjadi 4 level saja
    distance_sort="descending",
)

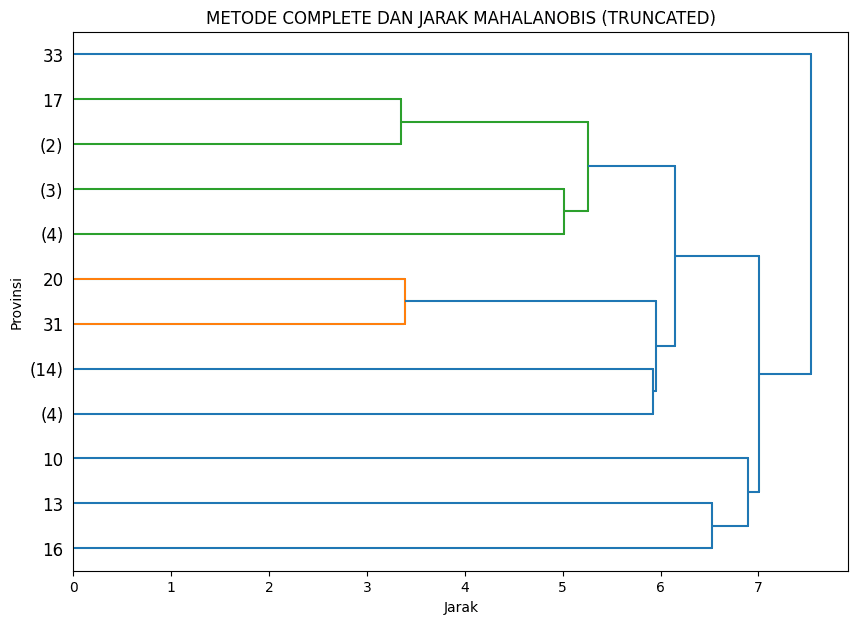
plt.title("METODE COMPLETE DAN JARAK MAHALANOBIS (TRUNCATED)")
plt.xlabel("Jarak")
plt.ylabel("Provinsi")
plt.show()

Pada hasil dendogram di atas, misal untuk hasil dari metode "ward" dengan jarak "euclidean" dan kita lakukan partisi pada jarak 8, maka akan menghasilkan 4 cluster. Cluster pertama terdiri dari 12 anggota mulai dari Gorontalo hingga Bengkulu, cluster ke-2 terdiri hanya 1 anggota yaitu Papua, cluster ke-3 terdiri dari 5 anggota dan cluster ke-4 terdiri dari 16 anggota. Pada contoh lainnya untuk metode "complete" dan jarak "mahalanobis" dan kita sajikan hanya sampai batas 4 level saja, maka dendogram akan menampilkan jumlah angota cluster tersebut, atau jika tunggal maka akan ditampilkan label (jika diberikan) atau nomor anggotanya.

Setelah cluster terbentuk, kita tentunya dapat memberikan label cluster ke dalam data asli yang dimiliki. Hal ini mungkin berguna untuk analisis lebih lanjut. Label cluster bisa kita peroleh menggunakan fungsi fcluster. Pelabelan diatur dengan menetapkan threshold. Nilai threshold dapat ditentukan dengan beberapa cara, misal dapat berupa jumlah maksimal cluster yang terbentuk, atau dapat juga berdasarkan batas jarak.Tiga parameter penting yang dapat diatur yaitu:

Z: Matriks linkage (output dari fungsi linkage)

t: menentukan threshold berdasarkan kriteria yang diberikan.

criterion: menentukan kriteria pembatasan. Misal "distance" maka banyaknya cluster dibatasi berdasarkan jarak threshold t yang diberikan. Jika "max_clust" maka jumlah cluster yang dibentuk maksimal sebanyak t cluster. Terdapat beberapa kriteria lain seperti "inconsistent" (default), "monocrit" dan "max_clust_monocrit".

Output dari fungsi ini adalah nomor cluster untuk indeks data yang bersesuaian ketika pembentukan cluster.

Mari kita gunakan dua jenis cluster sebelumnya untuk melihat pelabelan yang dihasilkan keduanya. Misal untuk yang pertama kita akan menggunakan criterion="maxclust" dan untuk yang kedua menggunakan criterion="distance".

from scipy.cluster.hierarchy import fcluster

# mengambil cluster dari hasil ward + eculidean
label_ward = fcluster(
    clust_ward_euclid, t=4, criterion="maxclust"   # membuat menjadi max. 4 cluster
)  

# mengambil cluster  dari hasil complete + mahalanobis
label_complete = fcluster(
    clust_comp_mahal, t=7, criterion="distance"    # membuat cluster dengan batas jarak 7
)  

data["label_ward"] = label_ward
data["label_complete"] = label_complete

print(data[["label_ward", "label_complete"]])

# OUTPUT

                           label_ward  label_complete
Provinsi                                             
Aceh                                3               1
Sumatera Utara                      1               1
Sumatera Barat                      3               1
Riau                                1               1
Jambi                               1               1
...                                 .               .
Maluku                              3               1
Maluku Utara                        3               1
Papua Barat                         3               1
Papua                               4               3

Setelah data dilabeli sesuai cluster, kita dapat melakukan berbagai analisis, baik itu ringaksan statistik maupun secara visual untuk melihat pola-pola dan perbedaan-perbedaan variabel berdasarkan clusternya.

Dari hasil tabulasi sederhana berikut ini, kita mungkin dapat melihat bagaimana keragaman antar cluster yang terbentukdengan metode ward, jarak euclidean serta kita gunakan sebanyak 4 cluster. Terlihat misalnya, cluster 2 memiliki rata-rata PDRB per kapita yang sangat tinggi, rata-rata IPM juga tertinggi, persentse kemiskinan terendah serta rata-rata persentase porok terendah. Cluster ini mungkin diisi oleh provinsi-provinsi yang memang sudah lebih maju.

# misal, kita gunakan 1 jenis saja yaitu ward + euclidean
data_ward = data.drop("label_complete", axis=1)

tabulasi_1 = data_ward.groupby("label_ward").mean()

print(f"Rata-rata nilai setiap peubah menurut cluster:\n")
print(tabulasi_1.transpose().round(2))

# OUTPUT

Rata-rata nilai setiap peubah menurut cluster:

label_ward             1          2         3         4
PDRB_KAPITA     64491.69  136195.20  42742.83  54051.00
IPM                71.56      77.94     69.24     60.62
TPT                 5.86       7.03      4.54      3.33
PST_KEMISKINAN      8.37       6.94     14.21     26.86
AHH_L              71.45      72.39     68.98     65.78
AHH_P              75.94      77.09     73.00     69.76
APS_07_12          99.39      99.63     99.02     83.43
APS_13_15          95.40      98.82     95.69     80.02
APS_16_18          71.81      82.46     77.68     63.98
APS_19_23          25.98      34.19     33.28     25.26
PST_PEROKOK        28.70      23.62     29.17     24.91

Silahkan mengeksplorasi lebih lanjut hasil di atas, misal dengan membuat boxplot sebaran masing-masing variabel berdasarkan cluster agar semakin jelas terlihat karakteristik pada masing-masing cluster. Silahkan juga melakukan analisis hierarchical clustering menggunakan metode agglomerative dengan linkage atau metrik jarak lainnya. Selamat mencoba!

• K-Means Clustering dengan Python
• Principal Component Analysis (PCA) dengan R

• Fungsi linkage [scipy.cluster.hierarchy.linkage]
• Fungsi dendogram [scipy.cluster.hierarchy.dendrogram]
• Fungsi fcluster [scipy.cluster.hierarchy.fcluster]
• Metrik Jarak [scipy.spatial.distance.pdist]

• Ananda, R. 2023. [RPubs – Unsupervised Learning: Cluster Analysis]
• Datanovia. [Hierarchical Clustering in R: The Essentials]
• James, G., Witten, D., Hastie, T., Tibshirani, R., and Taylor, J. 2023. An Introduction to Statistical Learning with Application in Python. Springer. [https://www.statlearning.com/]