K-Means Clustering dengan Python

Analisis cluster adalah metode statistik untuk mengelompokkan objek-objek yang memiliki karakteristik serupa ke dalam beberapa kelompok atau cluster tertentu. Tujuan utama dari analisis klaster adalah untuk memastikan bahwa objek-objek dalam satu klaster memiliki kesamaan yang tinggi satu sama lain, sementara antar cluster yang berbeda memiliki perbedaan yang signifikan. analisis custer memiliki penggunaan yang sangat luas meliputi berbagai bidang seperti pemasaran, biologi, pengenalan pola, pengolahan citra, dan pembelajaran mesin.
K-Means clustering adalah salah satu algoritma unsupervised learning yang populer dalam analisis data. Algoritma k-means mengelompokkan data dengan memisahkan sampel ke dalam n kelompok yang memiliki keragaman yang sama, dan meminimalkan kriteria tertentu yaitu Within Sum of Squared (WSS). K-means merupakan analisis cluster non-hierarkis dan memerlukan penentuan jumlah cluster sebelumnya.
Algoritma K-Means
Algoritma K-means Clustering membagi sekumpulan $N$ sampel $X$ ke dalam $K$ cluster-cluster terpisah, yang masing-masing dijelaskan oleh rata-rata ( $\mu_j$) sampel dalam cluster tersebut. Rata-rata ini sering disebut sebagai centroid cluster dan secara umum bukan merupakan titik dari $X$, meskipun berada dalam ruang yang sama.
Tujuan utama algoritma k-means adalah memilih centroid yang meminimalkan nilai WSS yaitu:
$$\sum_{i=1}^n \min_{\substack{ \ x_i \in C}}( || x_i – \mu_j ||^2)$$
Inisiasi Centroid
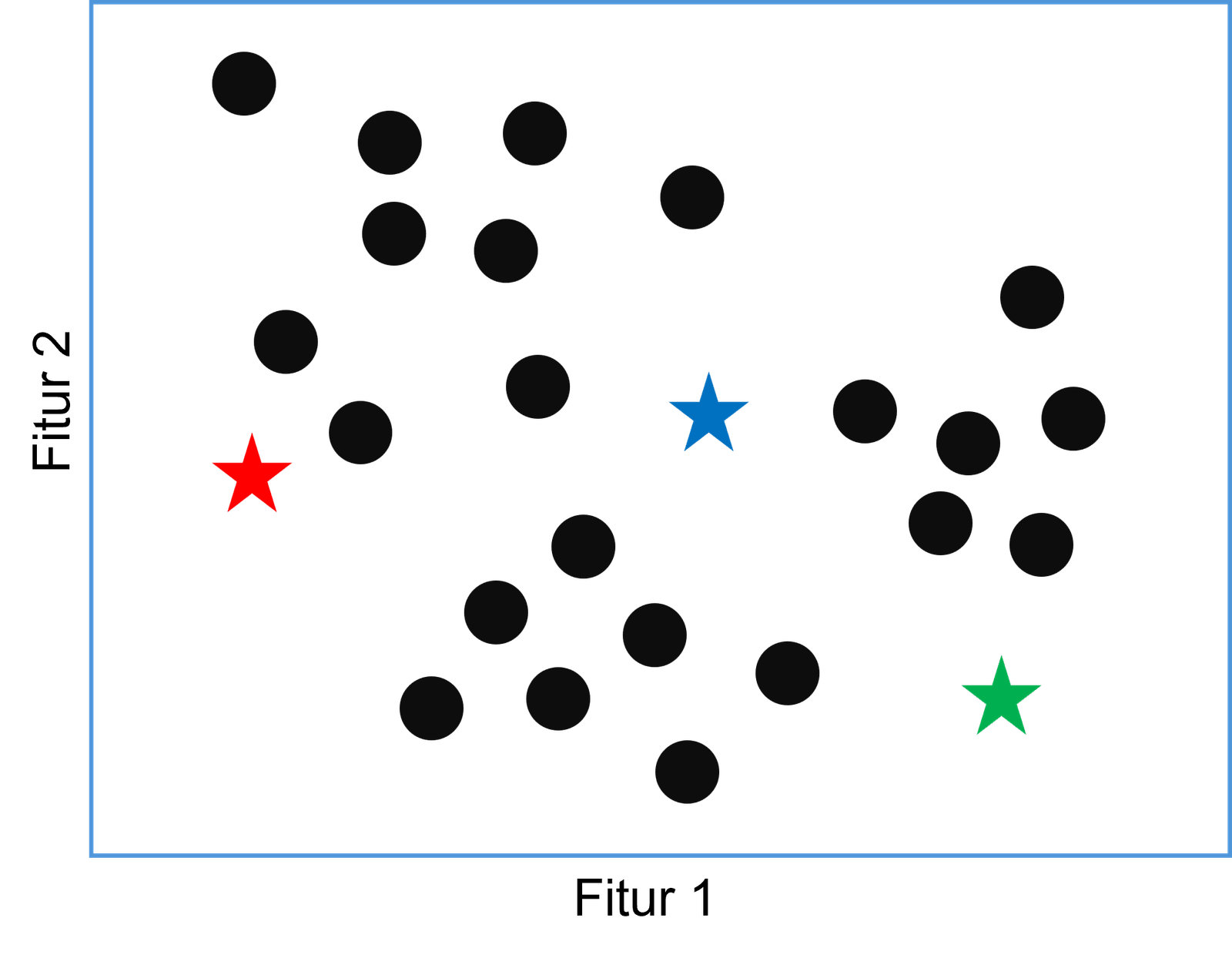
Langkah pertama dalam algoritma k-means adalah menginisialisasi pusat-pusat cluster awal dengan jumlah tertentu. Jumlah pusat klaster ini ditentukan sebelumnya oleh pengguna dan disebut sebagai $K$. Pusat-pusat cluster awal dapat diinisialisasi secara acak atau dengan metode khusus misalnya k-means++.
Ilustrasi pada gambar berikut menunjukkan penentuan 3 titik awal centroid yang diberikan secara acak.

Pembentukan Cluster
Setelah centroid awal sudah ditentukan, langkah berikutnya adalah mengelompokkan setiap titik ke dalam kelompok yang memiliki jarak ke centroid paling dekat. terdapat beragam metrik jarak yang dapat digunakan, misalnya yang paling umum yaitu jarak euclid.
Misal, diberikan dataset dengan N entri dan M fitur, jarak euclid masing-masing titik data ke centroid C dapat diberikan oleh persamaan berikut:
$$d(x_i, C) = \sqrt{\sum_{j=1}^{M} (x_{ij} – C)^2}$$
Untuk setiap titik data $x_i$ kita akan memiliki $K$ jarak, kemudian titik tersebut kita beri label sesuai centroid dengan jarak terkecil.
Gambar berikut mengilustrasikan bagaimana penentuan titik tertentu masuk ke dalam cluster berdasarkan jarak ke centroid terdekat. Dari hasil penghitungan, misal diperoleh bahwa data $x_1$ memiliki jarak terdekat dengan centroid ke-1 (berwarna biru).
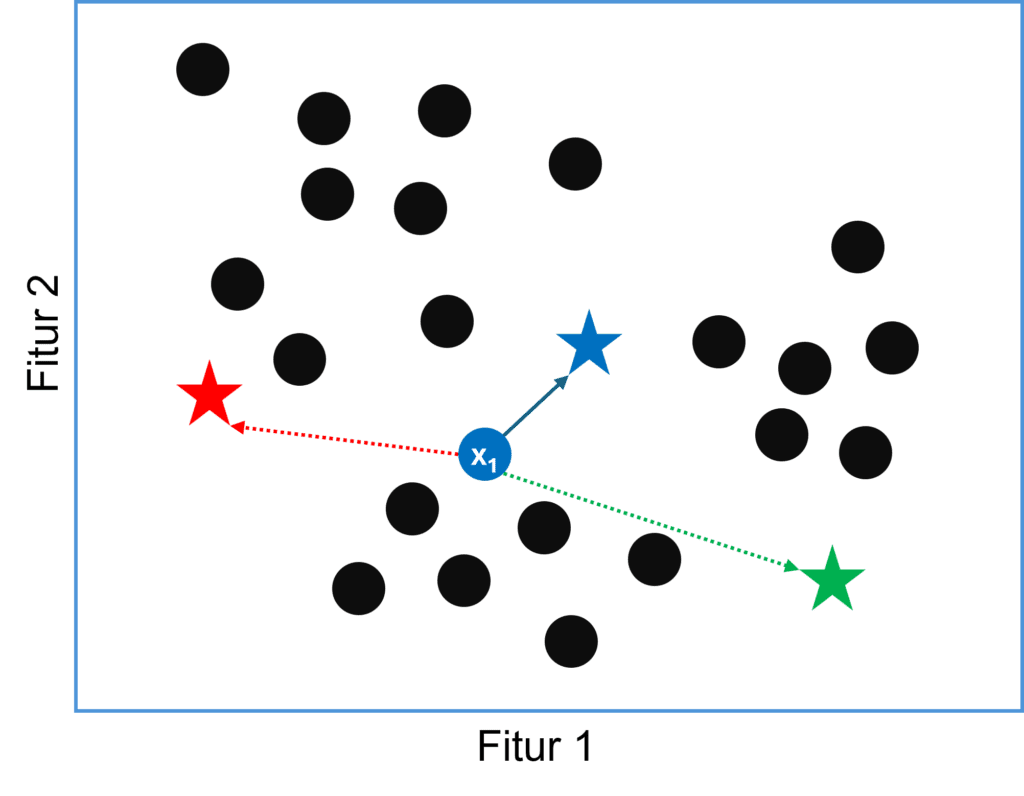

Proses penghitungan ini dilakukan untuk setiap titik data, sehingga setiap titik akan masuk pada salah satu dari 3 cluster dan diperoleh pengelompokan awal sebagai berikut:
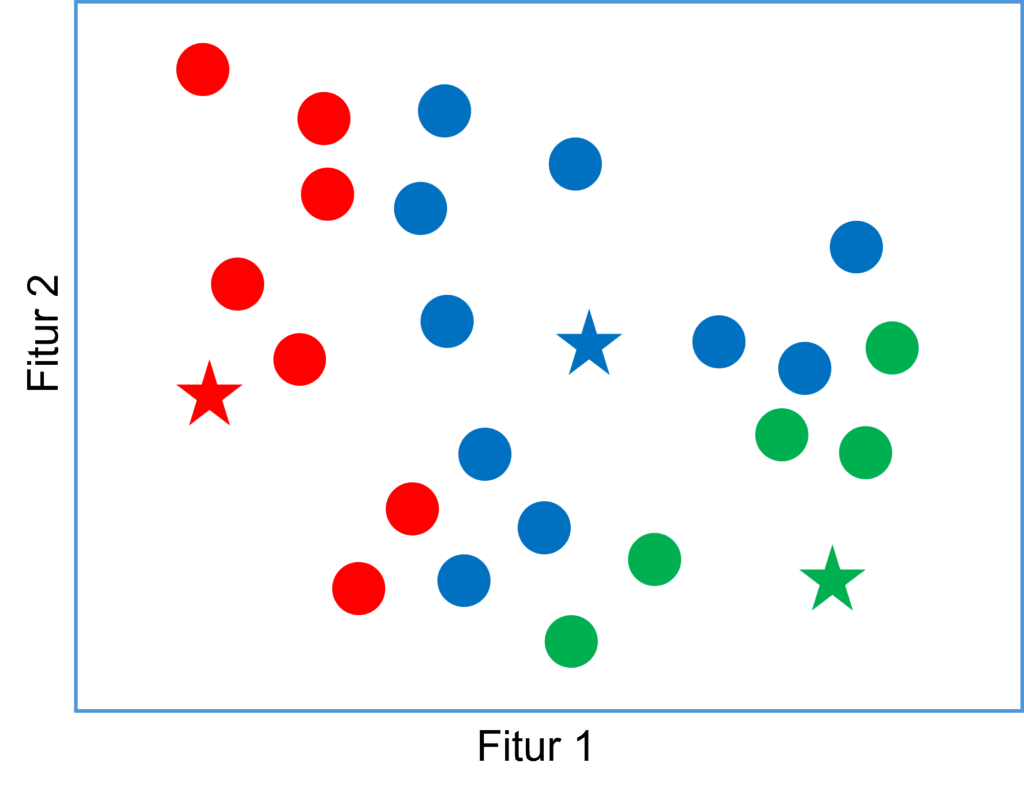

Pembaruan Centroid
Setelah semua data telah dikelompokkan, lokasi centroid akan diperbaharui. Centroid yang baru dihitung sebagai rata-rata dari semua titik data yang ada dalam kelompok tersebut. Dengan kata lain, centroid baru adalah titik tengah dari semua data dalam kelompok itu. Berikut adalah formula untuk menentukan lokasi centroid yang baru:
$$C_i=\frac{1}{|N_i|}\sum x_i$$
Hasil penghitungan tersebut selanjutnya akan menggeser lokasi ketiga centroid seperti yang ditampilkan pada gambar berikut:
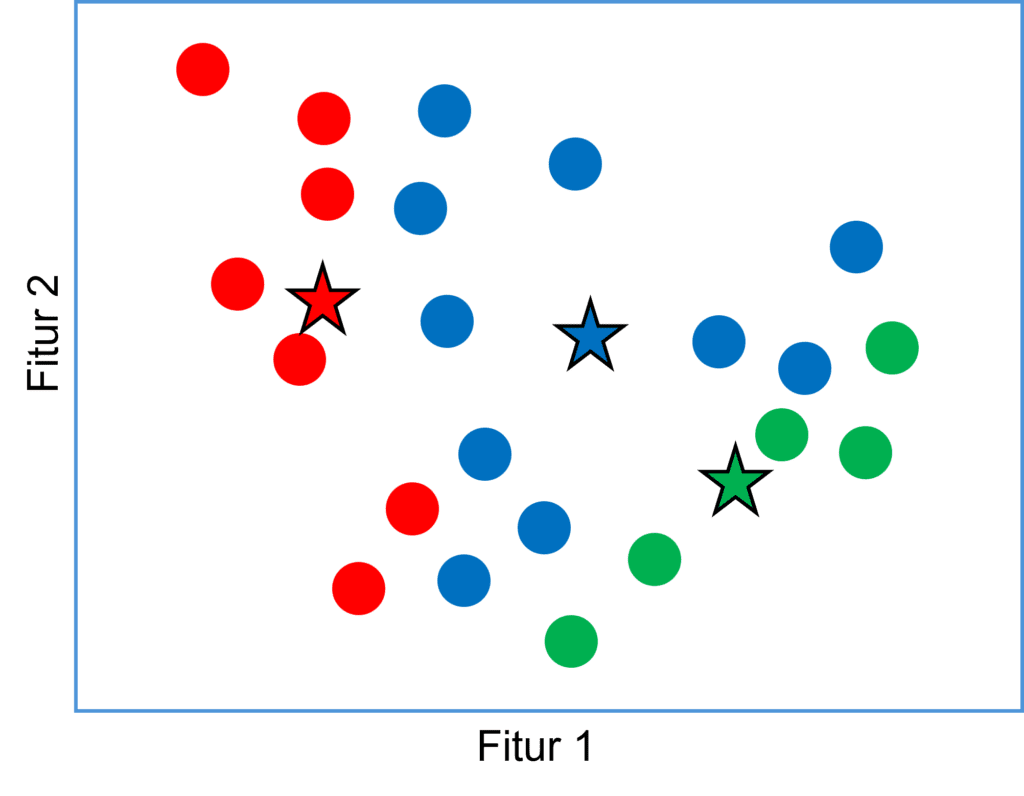

Berdasarkan lokasi centroid yang baru, maka dilakukan kembali langkah ke-2 yaitu mengukur kembali jarak setiap titik data ke lokasi centroid terbaru dan dilanjutkan dengan langkah ke-3 yaitu memasukkan data ke dalam cluster dengan centroid terdekat.
Pengecekan Konvergensi
Pengecekan dilakukan untuk memutuskan apakah iterasi dihentikan atau masih dilanjutkan. Konvergensi terjadi ketika tidak ada perubahan yang signifikan pada lokasi centroid (anggota setiap cluster sudah tidak berubah) atau ketika jumlah perubahan berada di bawah ambang tertentu. Jika konvergensi belum tercapai, algoritma kembali dilanjutkan ke langkah pengelompokan dan pembaruan lokasi centroid.
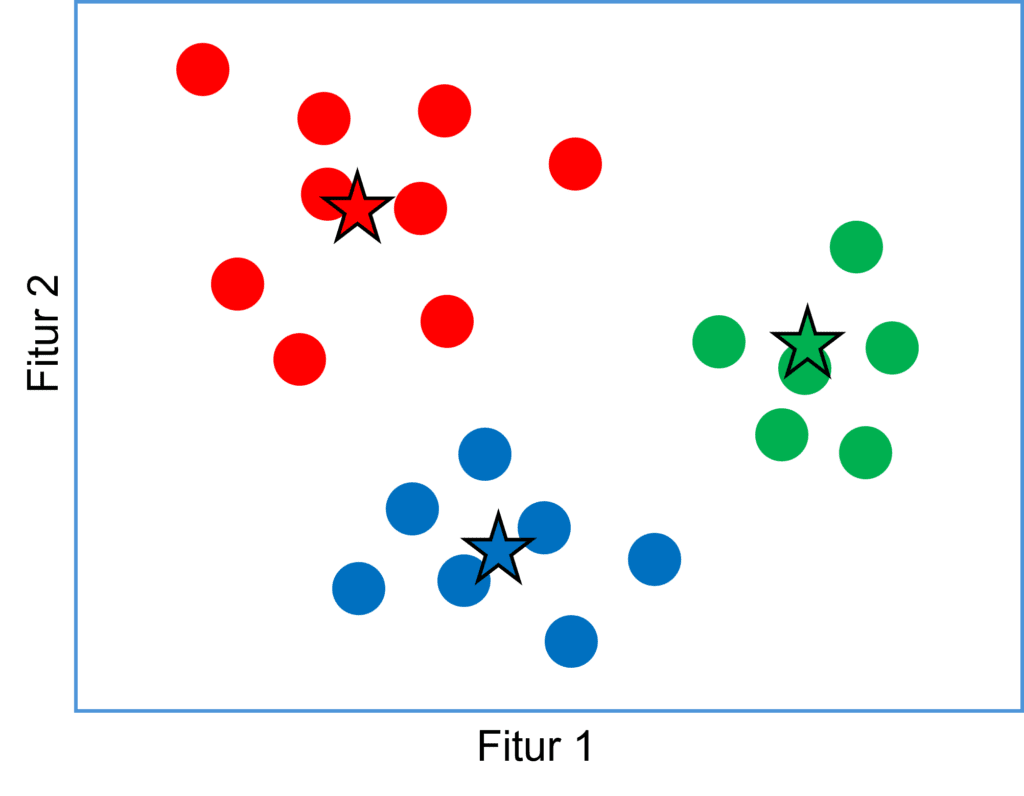

Gambar di atas menunjukkan hasil akhir iterasi di mana posisi centroid tidak bergeser lagi dikarenakan tidak terjadi perubahan anggota cluster lagi.
K-Means Clustering dengan Python
Untuk menerapkan algoritma k-means clustering dengan Python, kita dapat memanfaatkan pustaka scikit-learn yang sudah menyediakan implementasi yang efisien dan mudah digunakan dari algoritma clustering ini. Dengan scikit-learn, kita juga dapat dengan mudah memuat data, menyesuaikan model k-means, dan melakukan clustering pada data yang dimiliki.
Penyiapan Data
Jika anda memiliki data real yang ingin dianalisis, silahkan muat data tersebut menggunakan paket pandas atau paket lainnya. Pada tutorial ini, data yang akan digunakan adalah data simulasi. Data simulasi clustering dapat dibangkitkan menggunakan fungsi make_blobs dari modul scikit-learn.datasets. Pada contoh di bawah ini, kita membangkitkan 100 data dengan 3 variabel. Data dibangkitkan dengan kecenderungan mengelompok ke dalam 4 cluster. Nilai masing-masing variabel berkisar antara 10-20 dengan simpangan baku 0,8. Simpangan baku ini relatif kecil, sehingga pada masing-masing cluster memiliki data yang homogen. Hal ini kemungkinan akan menghasilkan pembagian cluster yang juga cukup tegas.
Python
import pandas as pd
import numpy as np
from sklearn.datasets import make_blobs
# Membuat data simulasi dengan 4 cluster dan 3 fitur
X, _ = make_blobs(
n_samples=100, # membangkitkan 100 data acak
centers=4, # data mengumpul ke dalam 4 cluster
center_box=(10, 20), # nilai data berkisar 10-20
cluster_std=0.8, # simpangan baku sekitar 0.8
n_features=3, # data memiliki 3 fitur/peubah
random_state=42,
)
data_sim = pd.DataFrame(np.round(X, 2), columns=["X1", "X2", "X3"])
print(data_sim)# OUTPUT
X1 X2 X3
0 9.63 19.19 15.23
1 10.00 18.83 16.05
2 18.39 9.06 19.35
3 17.17 11.23 19.23
4 14.03 18.99 17.61
.. ... ... ...
95 15.96 10.63 12.47
96 17.76 10.49 19.14
97 11.27 18.83 15.01
98 11.65 20.16 17.39
99 13.51 19.58 15.73
[100 rows x 3 columns]Data ini dapat kita visualisasikan juga menggunakan matplotlib untuk melihat bagaimana data menyebar.
Python
import matplotlib.pyplot as plt
# Menampilkan data
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c="blue", marker="o", s=50)
ax.set_xlabel("Fitur 1")
ax.set_ylabel("Fitur 2")
ax.set_zlabel("Fitur 3")
ax.set_title("Data Simulasi dengan 4 Cluster dan 3 Fitur")
plt.show()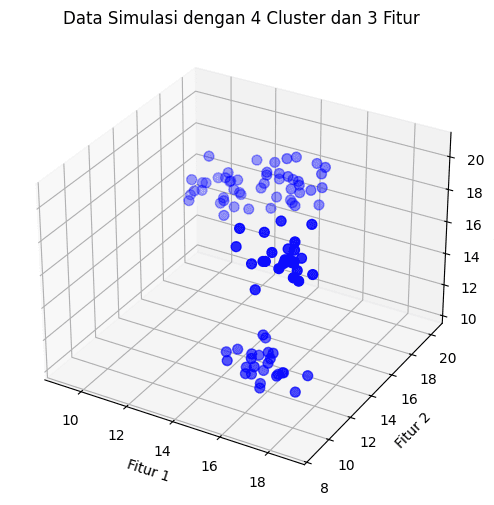

Scatter plot data simulasi (Gambar: penulis)
Standardisasi Data
K-means clustering merupakan algoritma yang sangat tergantung dengan jarak sehingga perbedaan satuan pada data akan sangat mempengaruhi hasil dan menjadi tidak optimal. Ketika terjadi kondisi demikian, langkah yang dapat dilakukan adalah melakukan standardisasi data. Standardisasi akan mentransformasi data sehingga memiliki skala yang sama, yaitu dengan rataan 0 dan simpangan baku 1. Cara lainnya, yaitu dengan menggunakan metrik jarak yang lebih robust terhadap perbedaan skala misalkan jarak mahalanobis.
Data simulasi ini sebenarnya memiliki skala data yang relatif sama. Namun agar setiap tahapan terjelaskan maka kita akan tetap melakukan standardisasi data. Proses ini dapat dilakukan menggunakan fungsi StandardScaler dari modul sklearn.preprocessing. Berikut cara melakukan standardisasi menggunakan fungsi StandardScaler:
Python
from sklearn.preprocessing import StandardScaler
# Inisialisasi StandardScaler
scaler = StandardScaler()
# mentransformasikan data dengan standardisasi
X_scaled = scaler.fit_transform(X)
print(f"Nilai rata-rata data scaled: {X_scaled.mean(axis=0)}")
print(f"Simpangan baku data scaled: {X_scaled.std(axis=0)}")# OUTPUT Nilai rata-rata data scaled: [-1.09356968e-16 1.71418435e-15 -1.61690106e-15] Simpangan baku data scaled: [1. 1. 1.]
Membuat Cluster
Untuk membuat model k-means scikit-learn menyediakan fungsi KMmeans. Fungsi ini memerlukan beberapa parameter yang bisa diatur, beberapa parameter utamanya adalah sebagai berikut:
n_clusters: jumlah cluster yang ingin dibuat (serta jumlah centroid yang dibangkitkan), nilai defaultnya adalah8cluster.init: metode inisiasicentroid, dapat berupak-means++(default), ataurandomatau dapat pula ditentukan secara langsung lokasinya pada nilai tertentu.max_iter: maksimal iterasi yang dilakukan, nilai defaultnya adalah300.tol: nilai minimal tolerasi perubahan skor antar iterasi agar proses tetap dilanjutkan, jika kurang dari nilai minimal tersebut maka iterasi dihentikan, nilai defaultnya1e-4alghoritm: algoritma k-means yang digunakan,lloyd(default) atauelkan.
Fungsi KMeans menghasilkan beberapa properti meliputi:
n_iter_: banyaknya iterasi yang dilakukan sampai berhenticluster_centers_: lokasi centroid pada setiap iterasiinertia_: metrik WSS atau jumlah kuadrat jarak dari setiap titik data ke pusat cluster terdekatnya.labels_: list yang berisi pembagian cluster setiap titik data
Python
from sklearn.cluster import KMeans
# Menginisialisasi model K-Means dengan jumlah kelompok (K)
kmeans = KMeans(n_clusters=4,
init="k-means++",
random_state=42)
# Menyesuaikan model dengan data yang telah disesuaikan skala
kmeans.fit(X_scaled)
# menampilkan beberapa properti hasil k-means
print(f"Jumlah iterasi: {kmeans.n_iter_}\n")
print(f"Centroid:\n {kmeans.cluster_centers_}\n")
print(f"Inertia: {kmeans.inertia_}\n")
# label (cluster) untuk masing-masing titik data
print(f"Cluster by data point:\n {kmeans.labels_}")# OUTPUT Jumlah iterasi: 4 Centroid: [[ 0.60314084 -0.83777107 -1.51478647] [-0.31519665 1.03799412 0.38955102] [ 1.10015636 -1.12569394 1.12313718] [-1.43280489 0.92078242 -0.0140456 ]] Inertia: 18.355352706603774 Cluster by data point: [3 3 2 2 1 2 3 0 0 2 0 2 1 0 1 3 0 0 0 0 1 3 1 3 3 2 3 1 1 1 0 3 1 2 2 3 1 0 2 0 2 1 0 2 0 1 2 2 0 1 1 0 0 3 0 1 0 1 3 1 0 1 0 0 3 3 2 3 3 1 2 3 1 3 0 3 1 2 2 3 2 0 1 3 2 2 2 2 1 0 2 2 1 3 1 0 2 3 3 1]
Visualisasi Cluster
Hasil k-means clustering selanjutnya dapat kita visualisasikan menggunakan scatter plot 3 dimensi (karena terdapat 3 variabel). Berdasarkan hasil plot di bawah ini, bisa kita lihat bagaimana algoritma k-means clustering mampu melakukan pengelompokan dengan sangat baik. Berdasarkan hasil sebelumnya, algoritma sudah konvergen hanya dengan 4 iterasi saja. Tentunya, hal ini tidak terlepas dari dataset yang kita bangkitkan memang sudah kita atur dengan pengelompokan yang cenderung tegas.
Python
# Mendapatkan label kelompok untuk setiap titik data
labels = kmeans.labels_
# Mendapatkan centroid dari setiap kelompok
centroids = kmeans.cluster_centers_
# Menampilkan data yang telah dikelompokkan dalam plot 3D
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
# membuat scatter plot data dan diwarnai sesuai label (c=labels)
scatter = ax.scatter(X_scaled[:, 0], X_scaled[:, 1], X_scaled[:, 2],
c=labels, marker='o', s=50, alpha=0.9)
# menampilkan lokasi centroids
centroids_plot = ax.scatter(centroids[:, 0], centroids[:, 1], centroids[:, 2],
c='red', marker='x', s=200)
legend1 = ax.legend(*scatter.legend_elements(), title="Clusters")
ax.add_artist(legend1)
plt.show()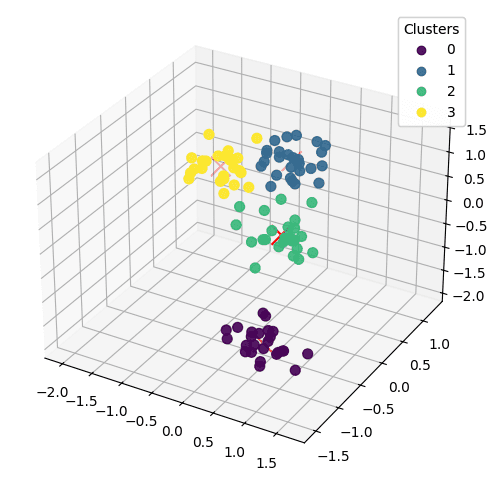

Scatterplot data menurut pembagian cluster (sumber: penulis)
Selain menggunakan scatterplot 3 dimensi, kita juga dapat membuat pairplot dari paket seaborn untuk menampilkan scatterplot antara setiap pasangan variabel. Visualisasi ini juga memberikan gambaran yang jelas bagaimana pengelompokan cluster jika dilihat berdasarkan 2 variabelnya. Plot di bawah ini menunjukkan karakteristik masing-masing cluster dengan lebih jelas. Misal, cluster ke-2 cenderung memiliki nilai X1 yang tinggi dan sebaliknya cluster ke-3 memiliki nilai X1 yang paling rendah. Contoh lainnya, untuk X2, cluster 0 dan 2 memiliki kecenderungan nilai yang sama dan jauh lebih rendah dibandingkan cluster 1 atau 3 yang juga cenderung sama. Informasi lainnya yang dapat dilihat yaitu Cluster 1 dan Cluster 3 terlihat memiliki jarak yang cukup dekat. Jika jumlah kluster dikurangi, maka kemungkinan kedua cluster ini akanmekelompok menjadi 1 cluster tersendiri.
Pada penelitian yang sebenarnya informasi ini tentu dapat memberikan insight yang luas. Misalkan penelitian yang bertujuan melakukan segmentasi pelanggan dengan variabel X1 merupakan informasi pendapatan. Tentu berdasarkan hasil ini dapat mengambil strategi yang berbeda untuk segmentasi yang berbeda. Untuk pelanggan pada cluster 3 misalnya, dapat ditawarkan diskon tambahan pada produk-produk tertentu yang sesuai agar menarik minat belanja mereka. Sementara untuk segmentasi dengan pendapatan yang jauh lebih tinggi, bisa jadi dengan menawarkan produk premium dan benefit tertentu atau sejenisnya.
Python
import seaborn as sns # Mengonversi data yang distandardisasi menjadi DataFrame df = pd.DataFrame(X_scaled, columns=['X1', 'X2', 'X3']) df['Cluster'] = labels # Membuat pair plot menggunakan seaborn sns.pairplot(df, hue='Cluster', palette='viridis', markers=["o", "s", "D", "P"]) plt.show()
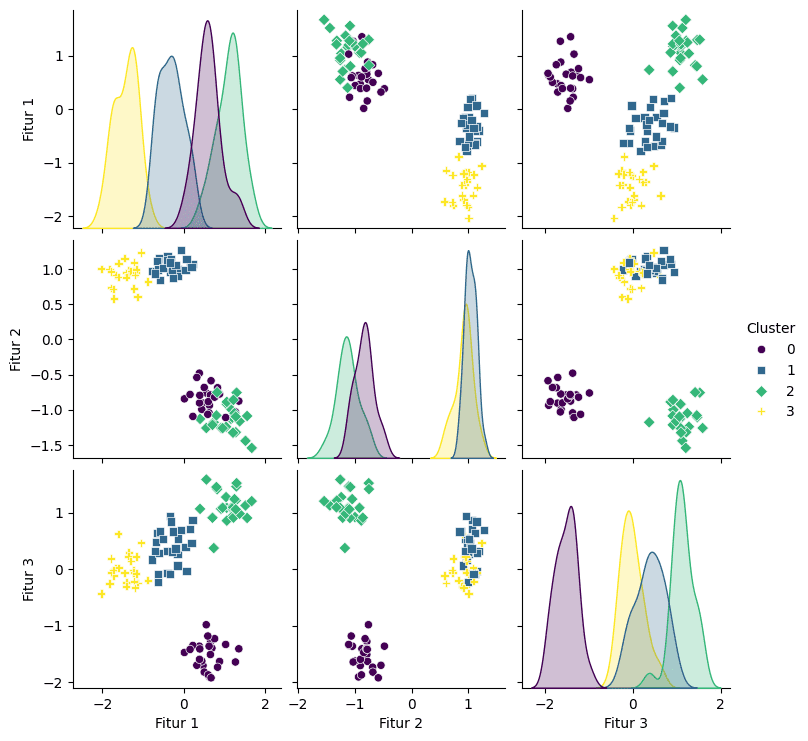

Scatterplot antar peubah (sumber: penulis)
Nilai k Optimal?
Penentuan nilai k pada algoritma k-means clustering sangat tergantung banyak faktor. Nilai ini mungkin ditentukan langsung berdasarkan kebutuhan, misalkan ingin mengelompokkan menjadi 4 kelompok, atau dengan alasan lainnya dan tentunya bisa juga bersifat subjektif.
Di lain sisi, nilai k juga dapat ditentukan menggunakan ukuran-ukuran teknis tertentu misalkan menggunakan elbow method ataupun silhoutte score.
Elbow Method
Elbow Method adalah teknik yang digunakan untuk menentukan jumlah klaster yang optimal dalam analisis cluster, khususnya saat menggunakan algoritma k-means. Metode ini membantu mengidentifikasi titik di mana penambahan klaster baru memberikan pengurangan yang signifikan lebih kecil dalamWSS dibandingkan dengan jumlah cluster sebelumnya. Dengan kata lain, metode ini mencari titik optimal di mana penambahan lebih banyak klaster tidak lagi memberikan peningkatan yang substansial dalam kualitas cluster.
Berikut adalah contoh kode untuk mengimplementasikan metode elbow :
Python
# Menentukan nilai k optimal
inertias = []
K_range = range(1, 10)
for k in K_range:
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X_scaled)
inertias.append(kmeans.inertia_)
# Plot inertia untuk berbagai nilai k
plt.figure(figsize=(8, 6))
plt.plot(K_range, inertias, marker='o', linestyle='-', color='b')
plt.xlabel('Number of Clusters (K)')
plt.ylabel('Inertia')
plt.title('Elbow Method for Optimal K')
plt.xticks(np.arange(1, 10, 1))
plt.yticks(np.arange(0, max(inertias) + 100, 100))
plt.tick_params(axis='both', direction='in', length=6, width=1)
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.grid(False)
plt.show()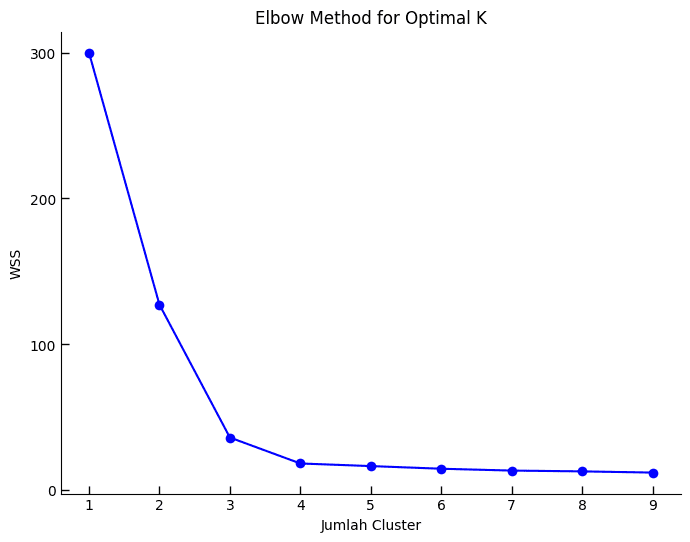

Melihat grafik di atas, sepertinya jumlah cluster terbaik yang dapat dipilih adalah 3 atau 4. Penurunan WSS dari 2 ke 3 sangat besar, sementara dari 3 ke 4 tidak besar namun masih dapat dianggap berarti. Sementara itu mulai k=4 dan lebih tinggi, penurunan nilai WSS sudah tidak begitu terlihat. Namun sekali lagi, penentuan jumlah cluster bisa jadi mempertimbangkan faktor lainnya, bukan sekedar teknis matematis saja.
Silhoutte Score
Silhouette Score adalah metrik yang digunakan untuk menilai kualitas clustering dengan mengukur seberapa mirip sebuah titik data terhadap cluster lainnya dibandingkan dengan cluster-nya sendiri. Nilai Silhouette memberikan indikasi tentang seberapa baik titik-titik data dikelompokkan, di mana nilai yang lebih tinggi menunjukkan klastering yang lebih baik.
Untuk setiap titik data $i$, Silhouette Score $s(i)$ dihitung dengan menggunakan dua nilai:
- a(i): Jarak rata-rata antara titik data $i$ dan semua titik data lainnya dalam cluster yang sama.
- b(i): Jarak rata-rata antara titik data $i$ dan semua titik data dalam cluster terdekat yang berbeda.
Silhouette Score $s(i)$ dihitung dengan formula:$s(i) = \frac{b(i) – a(i)}{\max(a(i), b(i))}$. Nilai $s(i)$ berkisar antara -1 dan 1:
- $s(i)$ mendekati 1: Titik data $i$ sangat cocok dengan cluster-nya.
- $s(i)$ mendekati 0: Titik data $i$ berada di atau dekat batas antara dua cluster.
- $s(i)$ mendekati -1: Titik data $i$ mungkin telah ditempatkan di cluster yang salah.
Melihat hasil di bawah ini, jumlah cluster yang paling optimal adalah 3 dengan rata-rata silhouette score tertinggi yaitu 0,76.
Python
from sklearn.metrics import silhouette_score
# Range nilai jumlah klaster yang ingin diuji
range_n_clusters = range(2, 11)
silhouette_scores = []
# Melakukan klastering K-Means untuk setiap nilai jumlah klaster
for n_clusters in range_n_clusters:
kmeans = KMeans(n_clusters=n_clusters, random_state=42)
labels = kmeans.fit_predict(X)
silhouette_avg = silhouette_score(X, labels)
silhouette_scores.append(silhouette_avg)
# Plot nilai Silhouette Score
plt.plot(range_n_clusters, silhouette_scores, marker='o')
plt.xlabel('Jumlah Cluster')
plt.ylabel('Average Silhouette Score')
# Menambahkan nilai Silhouette Score di dekat plot
for i, score in enumerate(silhouette_scores):
plt.text(range_n_clusters[i]+0.75, score, f"{score:.2f}", ha='right', va='bottom')
plt.grid(False)
plt.show()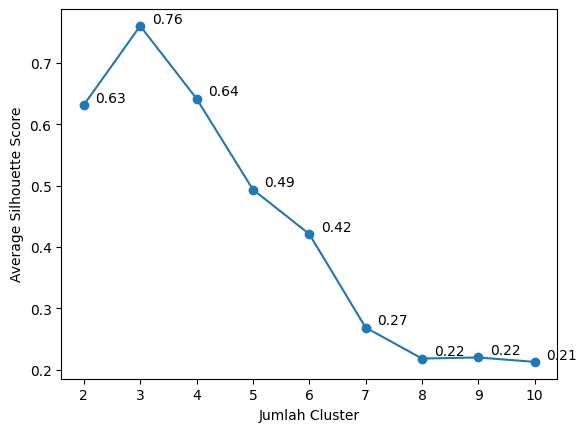

Rata-rata silhouette score pada berbagai jumlah cluster (gambar: penulis)
Tulisan Lainnya
- Hierarchical Clustering: Agglomerative Cluster dengan Python
- Principal Component Analysis (PCA) dengan R
Referensi
- Dokumentasi Fungsi KMeans: KMeans — scikit-learn 1.5.0 documentation
- Ananda, R (2023). RPubs – Unsupervised Learning: Cluster Analysis








