Support Vector Machine (SVM): Teori dan Konsep Dasar

Support Vector Machine (SVM) adalah algoritma supervised machine learning yang dapat digunakan untuk pemodelan klasifikasi maupun regresi. Misalnya untuk pengklasifikasian teks, analisis citra, deteksi spam, identifikasi tulisan tangan, analisis ekspresi gen, deteksi wajah hingga deteksi anomali atau pencilan pada data.

Tujuan utama dari algoritma SVM adalah menemukan hyperplane optimal dalam ruang p-dimensional yang dapat memisahkan titik-titik data dalam kelas-kelas yang berbeda di ruang fitur. Hyperplane mencoba untuk memastikan bahwa margin yang terbentuk antara titik-titik terdekat dari kelas yang berbeda sebesar mungkin. Dimensi hyperplane bergantung pada jumlah fitur. Jika jumlah fitur input adalah dua, maka hyperplane adalah sebuah garis. Jika jumlah fitur input adalah tiga, maka hyperplane berupa bidang 2 dimensi. Secara umum, untuk N buah fitur maka hyperplane akan berupa ruang p-1 dimensi.

Misalkan terdapat data dengan dua fitur yaitu X1 dan X2, serta label kelas R (Red) dan G (Green) seperti pada Gambar 1.

Pada contoh ini, ada sangat banyak garis yang bisa memisahkan titik data menjadi dua kelas, yaitu lingkaran merah dan hijau. Karena kita hanya mempertimbangkan dua fitur input yaitu X1 dan X2, maka garis-garis ini (L1, L2, L3, atau L4) adalah contoh hyperplane.

Contoh hyperplane pada Gambar 1 di atas dapat didefinisikan secara sederhana dengan persamaan garis sebagai berikut:

Dalam bentuk umum, pada data dengan p buah fitur, maka hyperplane dapat didefinisikan sebagai berikut:

Terdapat tiga kondisi yang mungkin terjadi yaitu:

• $W^T X+b=0$ (titik data tepat berada pada hyperplane)
• $W^TX+b>0$ (titik berada di atas hyperplane)
• $W^TX+b<0$ (titik berada di bawah hyperplane)

Dengan demikian, kita dapat menyatakan bahwa suatu hyperplane adalah persamaan yang membagi ruang p-dimensi menjadi 2 bagian. Jika berbicara pada konteks 2 dimensi, maka bagian tersebut adalah titik-titik data yang berada di atas garis hyperplane dan titik-titik data yang berada di bawah garis hyperplane.

Tujuan utama dari SVM adalah mencari hyperplane terbaik, yang memisahkan titik data secara maksimal. Maksimal di sini berarti bahwa garis yang dipilih harus memaksimalkan margin, yaitu jarak terdekat antara titik data dari dua kelas yang berbeda ke hyperplane. Titik-titik terdekat ini disebut dengan istilah support vectors.

Gambar 2, di mana merupakan contoh data yang terpisahkan dengan jelas dengan garis linier (linear separable data point) atau disebut juga Hard Margin atau Maximal Margin Classifier. Katakanlah L3 merupakan hyperplane terbaik karena menghasilkan margin maksimal.

Misal, kelas Red kita labeli dengan nilai 1 dan Green dengan nilai -1, berdasarkan n observasi ($x_1, x_2, \ldots, x_n \in \mathbb{R}^p$ dan setiap $x_i$ memiliki label $y_1, y_2, \ldots, y_n \in \{-1, \;1\}$, maka percarian hyperplane dengan margin maksimal merupakan solusi dari permasalahan optimasi berikut:

Di dunia nyata, kemungkinan hyperplane memisahkan data secara tegas hampir mustahil karena data sering kali tidak terdistribusi secara sempurna atau terpisah dengan jelas. Banyak data yang tumpang tindih atau mengandung noise, sehingga membuat pemisahan yang jelas dan sempurna tidak praktis. Oleh karena itu terdapat konsep Soft Margin Classifier atau Support Vector Classifier.

SVC memungkinkan beberapa titik data berada di sisi yang salah dari hyperplane, namun menambahkan penalti untuk setiap kesalahan ini. Tujuannya adalah sama yaitu menemukan solusi optimal yang memaksimalkan margin namun dengan tambahan kendala untuk meminimalkan total nilai kesalahan ($\sum{\epsilon_i^*}$). Nilai kesalahan ini ($epsilon$) disebut juga dengan istilah variabel slack.

Dengan adanya variabel slack ini, maka pencarian hyperplane optimal merupakan solusi dari masalah optimasi berikut:

SVC membagi dua kelas dengan batas linier. Namun, dalam praktiknya, seringkali kita menghadapi kasus di mana batas antar kelas tidak linier. SVC mengatasi hal ini dengan memperluas ruang fitur menggunakan fungsi kernel seperti polinomial (seperti kuadrat, kubik) atau fungsi kernel lainnya. Support Vector Machines (SVM) adalah perluasan dari SVC dengan mengekspansi dimensi ruang fitur melalui kernel-kernel ini.

Misalnya, seperti ilustrasi pada Gambar 4, ketika data asli dengan satu fitur tidak dapat dipisahkan oleh satu titik secara optimal. Kondisi ini dapat ditangani menggunakan kernel kuadratik (polinomial derajat 2) dan memetakan data tersebut ke ruang dua dimensi sehingga pemisahan menjadi lebih mudah dilakukan dengan hyperplane berupa sebuah garis.

Kernel adalah fungsi yang digunakan dalam SVM untuk memetakan data asli ke dalam ruang fitur yang berdimensi lebih tinggi. Hal ini memungkinkan SVM untuk mengidentifikasi hyperplane pada ruang fitur tersebut, ketika data sulit dipisahkan pada dimensi aslinya.

Beberapa fungsi kernel yang umum digunakan meliputi linear, polinomial, radial basis function (RBF), dan sigmoid.

Kernel linear menghitung dot product dari dua vektor input, yang sesuai dengan ruang fitur asli. Artinya, SVM dengan kernel linier sama saja dengan SVC. Penggunaan kernel linier cocok untuk masalah klasifikasi yang dapat dipisahkan secara linear.

Kernel polinomial menggunakan fungsi polinomial untuk memetakan vektor fitur ke dimensi yang lebih tinggi, memungkinkan pemisahan yang lebih kompleks.

Kernel RBF menggunakan fungsi Gaussian untuk mentransformasikan vektor fitur ke ruang fitur berdimensi tak hingga, dan dapat membantu dalam pemisahan data yang tidak linear.

Kernel sigmoid menggunakan fungsi sigmoid untuk memetakan vektor fitur ke ruang fitur non-linear, sering digunakan dalam neural network.

Kernel Fisher menggunakan informasi dari model probabilistik untuk mentransformasikan data, menghitung seberapa mirip dua vektor fitur dalam hal perubahan parameter model. Penggunaan kernel Fisher akan sangat efektif jika data dapat dimodelkan dengan distribusi probabilistik.

Pada bagian ini akan disajikan ilustrasi sederhana bagaimana algoritma SVM bekerja khususnya pada model klasifikasi. Untuk contoh penerapan secara lengkap dapat dilihat pada tulisan berikut:

[Support Vector machine (SVM) untuk Model Klasifikasi dengan Python]

Sebelum masuk ke pemodelan, kita akan membuat fungsi untuk menampilkan visualisasi dari hasil model SVM. Fungsi nantinya dapat digunakan berulang kali tanpa harus menulis kode yang sama untuk berbagai model yang dibangun.

# Fungsi untuk Memvisualisasikan hasil pemodelan SVM
import numpy as np
import matplotlib.pyplot as plt

def plot_svm_result(X, y, model, title):
    plt.figure(figsize=(8, 6))

    # membuat scatter plot
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap="coolwarm", s=75, edgecolors="k")

    # membuat batas keputusan
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()

    # membuat grid untuk evaluasi model
    xx = np.linspace(xlim[0], xlim[1], 30)
    yy = np.linspace(ylim[0], ylim[1], 30)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T
    Z = model.decision_function(xy).reshape(XX.shape)

    # Visualisasi batas keputusan
    ax.contour(
        XX, YY, Z, colors="k", levels=[-1, 0, 1], alpha=0.5, linestyles=["--", "-", "--"]
    )
    ax.contourf(XX, YY, Z, colors=["blue", "red"], alpha=0.2, levels=[Z.min(), 0, Z.max()])

    # Plot support vectors
    ax.scatter(
        model.support_vectors_[:, 0],
        model.support_vectors_[:, 1],
        s=100,
        linewidth=0.5,
        facecolors="none",
        edgecolors="k",
    )

    ax.set_xlabel("X1")
    ax.set_ylabel("X2")
    ax.set_title(title)

    plt.show()

Kode berikut ini menampilkan pemodelan SVM dari data simulasi yang diberikan. Data simulasi terdiri dari 2 peubah bebas yaitu X1 dan X2 serta peubah respon berupa kelas biner. Selanjutnya dilakukan pemodelan menggunakan SVM dengan kernel 'linear'.

Seperti yang dapat terlihat dari Gambar 5, data dapat dipisahkan cukup baik menggunakan kernel 'linear' tersebut dengan beberapa titik saja yang salah klasifikasi. Dengan demikian penggunaan kernel 'linier' sepertinya sudah cukup untuk memodelkan data yang ada tanpa perlu menggunakan kernel lainnya yang lebih kompleks.

Python

# Langkah 1: Impor paket yang diperlukan
from sklearn.datasets import make_blobs
from sklearn.svm import SVC

# Langkah 2: Membuat data simulasi dengan dua kelas
X, y = make_blobs(n_samples=100, centers=2, cluster_std=2.5, random_state=123)

# Langkah 3: Melatih model SVM dengan kernel linier
svm_linear = SVC(kernel="linear", random_state=42)
svm_linear.fit(X, y)

# Langkah 4: Visualisasi hasil SVM
plot_svm_result(X, y, svm_linear, "SVM dengan Kernel Linier")

Gambar 5. Visualisasi hasil model SVM dengan kernel linier (penulis)

Data simulasi pada contoh ini memiliki karakteristik yang berbeda dibandingkan sebelumnya. Dapat dilihat pada Gambar 6 bahwa data tidak dapat dipisahkan secara optimal menggunakan kernel linier berdasarkan X1 dan X2 saja. Model SVM yang dibangun menggunakan kernel 'linear' memberikan hasil yang buruk di mana terdapat banyak sekali data yang salah pengklasifikasian.

Python

# Langkah 1: Impor paket yang diperlukan
from sklearn.datasets import make_circles
from sklearn.svm import SVC

# Langkah 2: Membuat data simulasi
X, y = make_circles(n_samples=100, factor=0.5, noise=0.2, random_state=42)

# Langkah 3: Membuat dan melatih model SVM dengan kernel linier
svm_linear = SVC(kernel="linear", random_state=42)
svm_linear.fit(X, y)

# Langkah 4: Visualisasi hasil SVM
plot_svm_result(X, y, svm_linear, "SVM dengan Kernel Linier")

Gambar 6. Visualisasi hasil model SVM dengan kernel linier “Bad” (penulis)

Sekarang, mari kita coba membangun model SVM untuk data di atas mengunakan kernel 'poly' derajat 2. Hasil pada Gambar 7 menunjukkan model SVM jauh lebih baik dalam menentukan batas kelas, di mana jumlah data yang salah klasifikasi jauh lebih sedikit dibandingkan model dengan kernel 'linear'.

Python

# Gunakan data sebelumnya dan latih dengan SVM Kernel Polinomial

# Langkah 3: Membuat dan melatih model SVM dengan kernel polinomial
svm_poly = SVC(kernel="poly", degree=2, random_state=42)
svm_poly.fit(X, y)

# Langkah 4: Visualisasi hasil SVM
plot_svm_result(X, y, svm_poly, title="SVM dengan Kernel Polinomial Derajat 2")

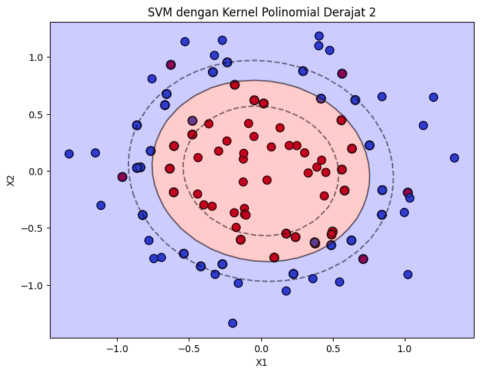
Gambar 7. Visualisasi hasil model SVM dengan kernel polinomial (penulis)

Seperti penjelasan pada bagian awal, penggunaan kernel ini memungkinkan model untuk mencari hyperplane pada ruang dimensi yang lebih tinggi. Data asli yang kita miliki tidak dapat dipisahkan secara linier pada ruang dua dimensi, sehingga penggunaan kernel polinomial akan mencari hyperplane pada ruang 3 dimensi. Hasil pada Gambar 8 berikut ini, dapat lebih memperjelas bagaimana model SVM dapat menemukan hyperplane dengan lebih baik pada ruang 3 dimensi tersebut.

Python

y_pred_poly = svm_poly.predict(X)

# Langkah 5: Visualisasi dalam 3 dimensi
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection="3d", )

# Plot data points
ax.scatter(X[:, 0], X[:, 1], y_pred_poly, c=y, cmap="coolwarm", s=50, edgecolors="k")

ax.set_xlabel("X1")
ax.set_ylabel("X2")
ax.set_zlabel("Prediksi")
ax.set_title("SVM dengan kernel polinomial derajat 2 (3D)")
plt.show()

Gambar 8. Tampilan 3-Dimensi model SVM dengan kernel polinomial (penulis)

• James, G., Witten, D., Hastie, T., Tibshirani, R., Taylor J. An Introduction to Statistical Learning with Application in Python. Springer. [https://www.statlearning.com]
• Dokumentasi Fungsi SVC Scikit-Lean: SVC — scikit-learn 1.5.0 documentation