Pohon Klasifikasi: Teori dan Konsep Dasar

Classification and Regression Tree (CART) adalah metode pembelajaran mesin yang digunakan untuk membuat model pembelajaran agar menghasilkan model prediksi. Pohon ini dapat digunakan untuk pemodelan klasifikasi (memprediksi kategori atau label) dan pemodelan regresi (memprediksi nilai kontinu).

Berdasarkan tipe data yang akan diprediksi, pohon keputusan untuk pemodelan klasifikasi umumnya disebut dengan pohon klasifikasi. Sebaliknya untuk pemodelan regresi disebut pohon regresi. Walaupun proses pembuatan pohon relatif sama, namun pada tulisan ini kita lebih fokus pada pohon keputusan untuk pemodelan klasifikasi. Oleh karena itu, terminologi yang akan digunakan pada bagian-bagian selanjutnya adalah “Pohon Klasifikasi”.

Dalam pohon klasifikasi, setiap node menunjukkan tes kondisi pada fitur, dan setiap cabang menunjukkan hasil dari tes tersebut. Leaf node atau daun pohon menunjukkan prediksi target. Pohon klasifikasi adalah salah satu metode pembelajaran mesin yang mudah dipahami dan diterapkan, karena visualisasi pohonnya mempermudah pemahaman dan interpretasi model.

Pohon klasifikasi memiliki beberapa karakteristik, di antaranya adalah:

1. Memiliki visualisasi yang jelas dan mudah dipahami, sehingga mempermudah pemahaman dan interpretasi model.
2. Dapat diterapkan pada berbagai jenis data, seperti data numerik, data kategorik, dan data mix, sehingga sangat versatile.
3. Kemampuan untuk membuat model yang akurat dan berguna untuk memprediksi target.
4. Memiliki proses pembelajaran yang efisien dan cepat, sehingga cocok untuk data dengan jumlah variabel yang besar atau data dengan jumlah sampel yang besar.
5. Menangani missing values dengan mengabaikan sample yang memiliki missing values atau dengan memberikan bobot pada sample yang memiliki missing values.
6. Dapat dilakukan pruning atau pemangkasan untuk membuat model lebih sederhana dan menghindari overfitting.

Terdapat beberapa komponen utama dalam pohon keputusan, yaitu:

1. Root node: Node pertama dan node teratas dalam suatu pohon klasifikasi. Ini adalah titik awal dari alur klasifikasi dan memiliki beberapa cabang yang mengarah ke node lain dalam pohon.
2. Intermediate node: Node ini adalah node yang berada di antara root node dan leaf node. Intermediate node berfungsi sebagai titik pemisahan untuk memisahkan data menjadi kelompok yang lebih kecil dan lebih spesifik. Masing-masing intermediate node memiliki atribut atau kriteria tertentu yang digunakan untuk memisahkan data yang berasal dari node sebelumnya.
3. Leaf node: Node ini adalah node yang berada di paling bawah pohon dan menunjukkan prediksi akhir. Leaf node merupakan node yang tidak memiliki cabang dan merupakan tempat dimana data diklasifikasikan ke dalam kelompok yang homogen. Setiap leaf node menggambarkan suatu label atau kategori akhir yang diterapkan pada set data yang diklasifikasikan ke dalam leaf node tersebut.
4. Branch: Branch adalah cabang atau jalur yang menghubungkan node satu dengan node lain dalam pohon. Setiap node dalam pohon memiliki beberapa cabang yang mengarah ke node lain dalam pohon, membantu untuk memisahkan data menjadi kelompok yang lebih kecil dan lebih spesifik. Branch menggambarkan pemisahan data berdasarkan atribut atau kriteria tertentu yang diterapkan pada setiap node.
5. Attribute: Fitur atau karakteristik dari suatu data yang digunakan dalam pohon klasifikasi untuk membuat pemisahan dan memprediksi label akhir. Pada setiap node dalam pohon klasifikasi, salah satu atribut dipilih untuk memisahkan data menjadi subkelompok yang lebih kecil lagi.
6. Splitting criteria: Kriteria yang digunakan untuk memutuskan bagaimana data harus dibagi menjadi subkelompok yang lebih kecil pada setiap node. Kriteria ini menentukan atribut atau fitur mana yang digunakan untuk memisahkan data pada setiap node dan membantu untuk memperkecil skala data serta membuat alur klasifikasi lebih mudah dipahami dan diinterpretasikan. Beberapa kriteria pemisahan yang sering digunakan dalam pohon klasifikasi termasuk entropy, gain ratio, dan gain information.
7. Decision rules: Aturan atau prosedur yang digunakan untuk memprediksi label akhir suatu data berdasarkan fitur atau atribut data tersebut. Decision rules dapat diambil dari setiap cabang dalam pohon klasifikasi dan merupakan pernyataan logika yang menentukan apakah data akan diklasifikasikan ke dalam satu label atau label lain. Contoh decision rule pada pohon klasifikasi adalah: “Jika usia < 30 tahun dan pendapatan < $50,000, maka klasifikasikan sebagai ‘tidak memiliki cicilan rumah’. Jika tidak, maka klasifikasikan sebagai ‘memiliki cicilan rumah’.”
8. Pruning: Proses memangkas atau menghilangkan cabang yang tidak penting atau kurang berguna dari pohon klasifikasi. Ini membantu untuk menghindari overfitting, yaitu situasi di mana pohon klasifikasi menjadi terlalu kompleks dan terlalu menyesuaikan dengan data pelatihan, sehingga membuatnya kurang efektif untuk memprediksi data baru. Dalam hal ini, cabang yang dihilangkan adalah cabang yang memiliki pengaruh minimal pada akurasi klasifikasi.

• Tahap 1: Mencari pemisahan/penyekatan (splitting) terbaik dari setiap variabel.
• Tahap 2: Menentukan variabel terbaik untuk penyekatan.
• Tahap 3: Melakukan penyekatan berdasarkan hasil dari Tahap 2, dan memeriksa apakah sudah waktunya menghentikan proses.
• Ketiga tahapan tersebut dilakukan untuk setiap simpul (node) dan hasil sekatannya.
• Proses pemisahan akan berhenti jika tercapai salah satu kriteria:
  • Simpul berisi amatan yang berasal dari satu kelas variabel respon. Misalnya semuanya Yes atau semuanya No.
  • Simpul berisi amatan yang seluruh variabel prediktornya identik. Misalnya semuanya usianya sama 20 tahun, jenis kelamin sama, pekerjaan sama.
  • Simpul berisi amatan yang kurang dari ukuran simpul minimal yang ditentukan di awal.
  • Kedalaman pohon sudah mencapai kedalaman maksimal.

Entropy dan Information Gain adalah dua konsep yang penting dalam pohon klasifikasi. Kedua konsep ini digunakan untuk mengukur ketidakpastian dan seberapa banyak informasi baru yang diperoleh setelah memisahkan data berdasarkan fitur tertentu.

1. Entropy: Ukuran ketidakpastian dalam set data. Nilai entropy berkisar antara 0 (data memiliki kepastian maksimal) dan 1 (data memiliki kepastian minimal). Entropy digunakan untuk menentukan seberapa efektif fitur tertentu dalam memisahkan data menjadi kelas yang berbeda.
2. Information Gain: Ukuran seberapa banyak informasi baru yang diperoleh setelah memisahkan data berdasarkan fitur tertentu. Nilai information gain berkisar antara 0 (tidak ada informasi baru yang diperoleh) dan 1 (informasi baru maksimal yang diperoleh). Fitur dengan information gain tertinggi dipilih sebagai fitur pemisahan pada node tertentu.

Kedua konsep ini digunakan bersama-sama dalam algoritma pohon klasifikasi untuk membuat aturan pemisahan yang membantu menentukan kelas dari data baru. Algoritma akan memilih fitur dengan entropy terendah atau information gain tertinggi sebagai fitur pemisahan pada setiap node, sehingga set data akan terpisah menjadi subsets yang lebih kecil dan lebih homogen dalam kelas target.

Andaikan sebuah gugus data D berisi individu-individu dengan dua kelas yaitu kelas YES dan NO, dengan proporsi YES sebesar p, dan NO sebesar (1-p).

Entropi dari gugus data tersebut adalah: $$E(D) = -p\ log_{2}(p)-(1-p)\log_{2}(1-p)$$ Gugus data yang seluruh amatannya dari kelas YES akan memiliki E(D) = 0. Gugus data yang seluruh amatannya dari kelas NO juga akan memiliki E(D) = 0. Entropi ini adalah ukuran keheterogenan data (impurity).

Berikutnya misalkan sebuah gugus data D dibagi menjadi beberapa kelompok, misalnya D1, D2, …, Dk berdasarkan variabel prediktor V, maka setiap $D_{i}$ bisa dihitung entropinya yaitu $E(D_{i})$.

Information Gain: $$IG(D,V)=E(D)-\sum_{i=1}^{k} \frac{|D_{i}|}{|D|}E(D_{i})$$ Semakin besar nilai information Gain maka variabel tersebut mampu memisahkan data menjadi kelompok-kelompok dengan anggota yang lebih homogen.

Misalkan terdapat contoh data seperti berikut:

pendidikan <- c("Rendah", "Rendah", "Sedang", "Sedang", "Tinggi",
                "Tinggi", "Sedang", "Rendah", "Tinggi", "Sedang")

usia <- c(40,35,45,30,35,40,30,45,40,40)

membeli <- c("Ya", "Tidak", "Ya", "Tidak", "Tidak",
             "Ya", "Ya", "Ya", "Ya", "Tidak")

data <- data.frame(pendidikan, usia, membeli)

print(data)

# OUTPUT

   pendidikan usia membeli
1      Rendah   40      Ya
2      Rendah   35   Tidak
3      Sedang   45      Ya
4      Sedang   30   Tidak
5      Tinggi   35   Tidak
6      Tinggi   40      Ya
7      Sedang   30      Ya
8      Rendah   45      Ya
9      Tinggi   40      Ya
10     Sedang   40   Tidak

Berdasarkan formula Entropy dan Information Gain maka kita dapat membuatnya dalam bentuk fungsi sebagai berikut:

# Fungsi Entropy
entropy <- function(n, n1) {
  p <- n1/n
  ed <- (-p*log2(p))-(1-p)*log2(1-p)

  return (ifelse(ed=="NaN", 0, ed))
}

# Fungsi Information Gain
inf.gain <- function(n.awal, n1.awal, n.bag1, n1.bag1){
  ED.awal <- entropy(n.awal, n1.awal)
 
  ED.bag1 <- entropy(n.bag1, n1.bag1)
  
  n.bag2 <- n.awal - n.bag1
  n1.bag2 <- n1.awal - n1.bag1

  ED.bag2 <- entropy(n.bag2, n1.bag2)
  
  IG <- ED.awal - ((n.bag1/n.awal)*ED.bag1)-((n.bag2/n.awal)*ED.bag2)
  
  return(IG)
}

Tahap 1:

Mencari pemisahan partisi terbaik untuk variabel pendidikan. Kemungkinan paritisi:

1. Pendidikan: Rendah vs (Sedang, Tinggi)
2. Pendidikan: (Rendah, Sedang) vs Tinggi

Adapun untuk variabel usia kemungkinan partisinya adalah sebagai berikut:

1. Usia: <= 30 vs > 30
2. Usia: <= 35 vs > 35
3. Usia: <= 40 vs > 40

Berdasarkan informasi di atas, kita akan mencari partisi terbaik dari masing-masing variabel. Dari output di bawah ini, diperoleh Information Gain tertinggi untuk variabel pendidikan adalah dengan partisi menjadi (Rendah, Sedang) vs Tinggi dengan nilai 0.01997. Sementara itu untuk variabel usia adalah <= 35 vs > 35 dengan nilai 0.25642.

# Pendidikan
pp1 = inf.gain(10, 6, 3, 2)    # Rendah vs (Sedang,Tinggi)
pp2 = inf.gain(10, 6, 6, 4)    # (Rendah, Sedang vs Tinggi)
paste("Pendidikan:")
cat(">>> Rendah vs (Sedang, Tinggi):", pp1, "\n")
cat(">>> (Rendah, Sedang) vs Tinggi:", pp2, "\n\n")

# Usia
pu1 = inf.gain(10, 6, 2, 1)    # Usia <= 30 vs Usia > 30
pu2 = inf.gain(10, 6, 4, 1)    # Usia <= 35 vs Usia > 35
pu3 = inf.gain(10, 6, 8, 4)    # Usia <= 40 vs Usia > 40
paste("Usia:")
cat(">>> Usia <= 30 vs Usia > 30:", pu1, "\n")
cat(">>> Usia <= 35 vs Usia > 35:", pu2, "\n")
cat(">>> Usia <= 40 vs Usia > 40:", pu3, "\n")

# OUTPUT

'Pendidikan:'
>>> Rendah vs (Sedang, Tinggi): 0.005802149 
>>> (Rendah, Sedang) vs Tinggi: 0.01997309 

'Usia:'
>>> Usia <= 30 vs Usia > 30: 0.007403392 
>>> Usia <= 35 vs Usia > 35: 0.2564259 
>>> Usia <= 40 vs Usia > 40: 0.1709506

Tahap 2:

Pada tahapan ini, partisi tertinggi untuk masing-masing variabel dibandingkan. Berdasarkan hasil sebelumnya maka diperoleh partisi terbaik adalah menggunakan variabel usia dengan partisi <= 35 vs > 35.

Tahap 3:

Setelah ditentukan variabel dan partisi yang akan digunakan, lakukan penyekatan simpul berdasarkan usia (dengan batas 35 tahun). Pada tahapan ini maka data dibagi ke dalam dua simpul. Simpul pertama berisi amatan dengan nilai variabel usia <= 35 dan simpul ke-2 yaitu amatan dengan nilai variabel usia > 35.

Berdasarkan gambar hasil penyekatan, pada simpul dengan nilai usia <= 35 terdapat 4 amatan, dimana 3 amatan memiliki label “Tidak”. Sementara itu, pada simpul dengan nilai usia > 35 terdapat 6 amatan dengan 5 diantaranya memiliki label “Beli”.

Misalkan penyekatan hanya kita lakukan sekali saja seperti hasil di atas, maka kita dapat memprediksi apakah seseorang akan membeli atau tidak berdasarkan pohon tersebut. Contoh, jika terdapat seseorang dengan pendidikan="Sedang" dan usia=37 Tahun, berdasarkan pohon ini, orang tersebut akan diprediksi masuk ke dalam kategori “Beli”. Sebaliknya jika seseorang memiliki pendidikan="sedang" dan usia=20 tahun, maka akan diprediksi sebagai kategori “Tidak”.

Dalam praktiknya, dengan jumlah data yang lebih banyak, tentu saja proses penyekatan tidak hanya berlangsung sekali. Pada setiap simpul yang dihasilkan dapat dilakukan kembali proses yang sama seperti pada tahap 1 sampai tahap 3. Proses akan berhenti apabila setiap simpul sudah berisi amatan yang homogen, atau tergantung pengaturan nilai-nilai hiperparameter yang akan mengontrol kapan penyekatan dihentikan.

Dalam membangun pohon klasifikasi, terdapat beberapa parameter atau hiperparameter yang dapat diatur sedemikian rupa untuk mengoptimalkan performa model. Berikut adalah beberapa hiperparameter penting pada pohon klasifikasi:

1. Maximum Depth: Ini adalah parameter yang menentukan maksimal kedalaman pohon. Nilai yang lebih besar akan menghasilkan pohon yang lebih kompleks, tetapi juga memiliki risiko overfitting.
2. Minimum Samples per Leaf: Ini adalah parameter yang menentukan jumlah minimum sampel data pada setiap daun. Nilai yang lebih besar akan membuat model lebih stabil, tetapi juga akan menghasilkan pohon yang lebih sederhana.
3. Minimum Samples per Split: Ini adalah parameter yang menentukan jumlah minimum sampel data yang diperlukan untuk membuat split pada pohon. Nilai yang lebih besar akan membuat model lebih stabil, tetapi juga akan menghasilkan pohon yang lebih sederhana.
4. Maximum Features: Ini adalah parameter yang menentukan jumlah maksimal fitur yang digunakan pada setiap split. Nilai yang lebih kecil akan membuat model lebih stabil, tetapi juga akan menghasilkan pohon yang lebih sederhana.
5. Maximum Leaf Nodes: Ini adalah parameter yang menentukan jumlah maksimal daun pada pohon. Nilai yang lebih besar akan menghasilkan pohon yang lebih kompleks serta memiliki risiko overfitting.

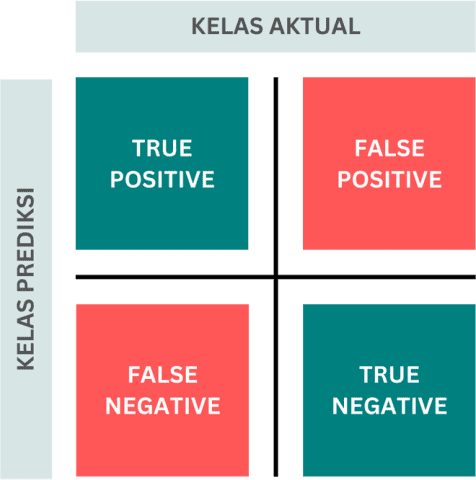
Untuk mengetahui bagaimana kemampuan model dalam melakukan prediksi, terdapat beberapa metrik yang dapat digunakan. Secara umum setiap metrik akan mengukur berapa banyak data yang diprediksi secara tepat dari seluruh data yang diuji. Pada contoh klasifikasi dengan dua kelas, representasi hasil prediksi dapat dijelaskan dalam terminologi sebagai berikut:

• True Positive: banyaknya amatan dari kelas positif yang diprediksi benar sebagai kelas positif
• True Negative: banyaknya amatan kelas negatif yang diprediksi benar sebagai kelas negatif
• False Positive: banyaknya amatan yang diprediksi salah sebagai kelas positif dimana sebenarnya adalah kelas negatif
• False negatif: banyaknya amatan yang diprediksi salah sebagi kelas negatif dimana sebenarnya adalah kelas positif

berdasarkan terminologi di atas, berikut adalah beberapa metrik yang dapat digunakan untuk menilai kemampuan prediksi dari suatu model pohon klasifikasi:

1. Akurasi: Akurasi mengukur seberapa baik model tersebut mengklasifikasikan data baru dengan benar. Akurasi didefinisikan sebagai rasio jumlah prediksi yang benar terhadap jumlah total prediksi yang dibuat oleh model. $$Akurasi = \frac{TP + TN}{amatan}$$
2. Presisi: Mengukur seberapa sering model membuat prediksi positif yang benar. Presisi didefinisikan sebagai rasio jumlah prediksi positif yang benar terhadap jumlah total prediksi positif yang dibuat oleh model. $$Presisi = \frac{TP}{TP+FP}$$
3. Sensitivitas/Recall: Digunakan untuk mengukur seberapa baik model tersebut menemukan seluruh kelas positif yang ada. Sensitivity/Recall didefinisikan sebagai rasio jumlah kelas positif yang benar terdeteksi oleh model terhadap jumlah total kelas positif dalam data. $$Sensitivitas = \frac{TP}{TP+FN}$$
4. Spesifisitas: Digunakan untuk mengukur seberapa baik model tersebut membedakan antara kelas negatif dan kelas positif. Specificity didefinisikan sebagai rasio jumlah kelas negatif yang benar terdeteksi oleh model terhadap jumlah total kelas negatif dalam data. $$Spesifisitas = \frac{TN}{TN+FP}$$
5. F1-Score: mengukur keseimbangan antara precision dan recall. Jika precision dan recall bernilai tinggi, maka F1-score juga akan tinggi, yang menunjukkan bahwa model memiliki kinerja yang baik dalam memprediksi kelas positif dan menemukan kelas positif yang sebenarnya. $$F1-Score = 2\frac{Sensitivitas*Presisi}{Sensitivitas+Presisi}$$
6. AUC (Area Under the Curve) ROC (Receiver Operating Characteristic): mengukur kemampuan model dalam membedakan antara amatan positif dan negatif. AUC ROC adalah luas area di bawah kurva ROC, dimana semakin luas area tersebut berarti semakin baik kemampuan model dalam membedakan amatan positif dan negatif.

Lihat juga: Metrik Evaluasi untuk Model Klasifikasi

Performa model idealnya diukur berdasarkan prediksi terhadap data baru/ data uji. Namun sebagai ilustrasi saja, jika mengambil contoh model sebelumnya, berdasarkan 10 data tersebut akan diperoleh hasil sebagai berikut: TP=5, TN=3, FP=1, FN=1.

Adapun nilai akurasi dari model adalah $$Akurasi=\frac{5+3}{10}=0.8$$

Nilai ini menunjukkan bahwa model mampu memprediksi secara tepat 80% kelas dari data yang ada.

Selanjutnya: Pemodelan Pohon Klasifikasi dengan Rpart

• Foley, M. (July 26, 2020): Classification Tree
• Guild, C. (August 28, 2021): Classification and Regression Trees (CART) in R
• Rizki Ananda (November 1, 2023): Pohon Klasifikasi (CART)