Permutation Importance untuk Penentuan Peubah Penting dengan Python

Salah satu isu yang menjadi perhatian pada model-model machine learning adalah mengenai interpretabilitas. Idealnya, setiap peneliti tidak hanya mengharapkan performa model yang optimal tetapi juga mudah dipahami. Untuk beberapa alasan, umumnya model menjadi jauh lebih dipercaya jika kita mengetahui faktor yang mendasari suatu model dalam pengambilan keputusan (Drobnič et al., 2020).

Features Importance merupakan ukuran yang menunjukkan besar kecilnya kepentingan atau kontribusi peubah dalam perubahan performa model. Salah satu ukuran yang dapat digunakan yaitu Permutation Importance. Permutation Importance mengukur besarnya perubahan performa model, ketika nilai-nilai pada satu peubah tertentu dilakukan permutasi acak (Altmann et al., 2010). Permutation Importance bersifat model agnostik, sehingga dapat diterapkan pada berbagai algoritma pemodelan.

Intuisi dibalik permutation importance adalah Jika nilai pada peubah tersebut diacak namun performa model tidak berubah, ini menunjukkan berapapun nilai peubah tersebut tidak begitu berpengaruh. Sebaliknya, jika performa model mengalami penurunan yang besar, maka dapat diyakini nilai peubah tersebut sangat mempengaruhi kemampuan model dalam memprediksi.

Penghitungan permutation importance pada satu peubah dapat dilakukan berulang kali. Dengan demikian, kita tidak hanya memperoleh satu nilai tertentu, namun dapat melihat dalam bentuk selang nilai. Selain itu, proses komputasi permutation importance juga sangat cepat, karena tidak memerlukan proses training model berkali-kali. Performa diukur hanya pada 1 model, namun dengan nilai peubah yang telag dilakukan permutasi acak.

Ilustrasi pada Gambar 1 menunjukkan suatu model dengan 4 peubah prediktor dan peubah respon bertipe kategorik dengan 3 kategori. Model mampu memprediksi nilai dari dataset dengan akurasi sebesar 0,8.

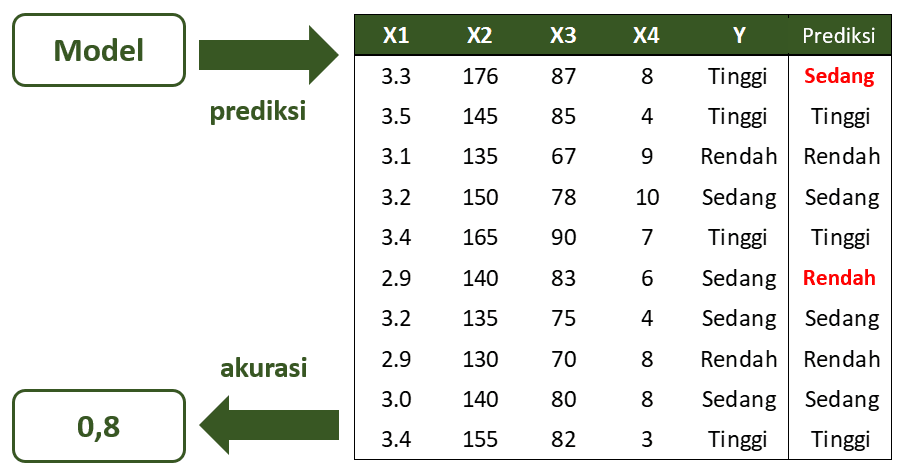
Sebagai contoh, untuk menghitung nilai permutation importance pada peubah X1:

• lakukan permutasi acak untuk nilai peubah X1,
• dengan menggunakan model yang sama, prediksi kembali output dari data yang sudah diacak,
• hitung nilai akurasi dari prediksi yang diperoleh,
• banndingkan nilai akurasi dengan nilai akurasi pada data asli,
• proses dapat dilakukan berulang kali untuk memberikan gambaran hasil yang lebih umum,
• jika dilakukan secara iteratif, maka permutation importance diukur berdasarkan nilai rata-rata dari setiap iterasi.

Gambar 2 di bawah ini mengilustrasikan permutasi acak pada nilai-nilai peubah X1. Akurasi model setelah data X1 diacak menjadi lebih rendah dibandingkan sebelumnya. Penurunan ini menunjukkan bahwa peubah X1 memiliki pengaruh yang besar di dalam model.

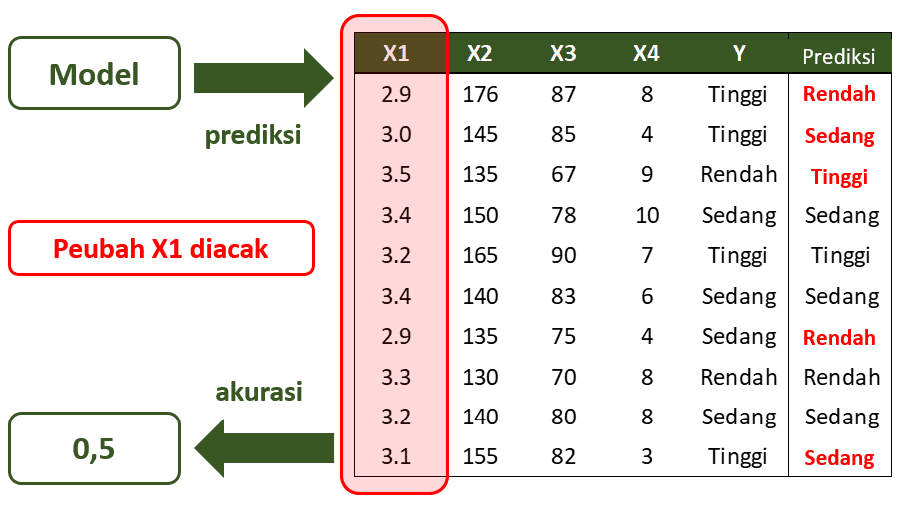
Untuk membandingkan tingkat kepentingan setiap peubah pembentuk model, maka lakukan proses yang sama untuk peubah lainnya. Peubah dengan nilai permutation importance yang lebih besar berarti memiliki pengaruh lebih besar pula pada model tersebut.

Permutation importance memiliki kelemahan ketika adanya kondisi multikolinearitas, atau hubungan yang kuat antar peubah prediktor. Pada kondisi semacam ini, terdapat kemungkinan peubah yang seharusnya memiliki pengaruh besar dianggap tidak berpengaruh. Hal ini disebabkan performa model yang tidak berkurang banyak karena sudah terwakili oleh peubah lainnya yang memiliki korelasi tinggi.

Pada bagian ini kita akan mencoba menghitung permutation importance pada model prediksi kelas wine. Dataset yang digunakan tersedia pada modul sklearn.datasets sehingga dapat langsung digunakan. Total sampel pada dataset sebanyak 178, dengan 13 peubah prediktor bertipe numerik dan peubah respon dengan 3 kelas (0, 1 dan 2).

Model yang akan digunakan dalam contoh ini adalah Gradient Boosting. Namun seperti yang sudah disampaikan di awal, permutation importance dapat digunakan untuk model apapun.

Proses training akan menggunakan sebanyak 70% sebagai data dan sisanya sebanyak 30% sebagai data testing untuk mengevaluasi performa model.

Kita tidak melakukan tuning hyperparameter apapun, karena fokus tulisan ini adalah pada penghitungan permutation importance bukan tentang pencarian model terbaik. Parameter model dibuat dengan pengaturan jumlah pohon 100 dan learning rate 0.01. Nilai akurasi (mean accuracy) yang diperoleh menggunakan data testing adalah 0,963.

# membaca dataset wine
from sklearn.datasets import load_wine
# Membagi data training dan testing
from sklearn.model_selection import train_test_split
# Membuat model GradientBoosting untuk Klasifikasi
from sklearn.ensemble import GradientBoostingClassifier

# membaca dataset wine
wine = load_wine(as_frame=True)

X = wine.data
y = wine.target

# Membagi data (training: 70%, testing: 30%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y, random_state=111)

# Membuat Model Gradient Boosting
# Jumlah Pohon: 100, Learning Rate = 0.01, Lainnya: Default
model_gb = GradientBoostingClassifier(n_estimators=100, learning_rate=0.01)
model_gb.fit(X_train, y_train)

Print("Skor Akurasi:", model_gb.score(X_test, y_test))

# Output
# 0.9629629629629629

Untuk menghitung permutation importance kita menggunakan fungsi permutation_importance dari modul sklearn.inspection. Beberapa parameter penting yang perlu dtentukan adalah:

• estimator: model yang akan dihitung nilai permutation importance,
• X: DataFrame atau Array yang berisi data peubah prediktor (features)
• y: Peubah target
• n_repeats : jumlah ulangan untuk setiap peubah X (default: 5)

Pada kode berikut kita akan menggunakan 100 kali ulangan. Adapun performa yang akan diukur adalah performa model pada data testing, sehingga parameter X dan y kita isi dengan data testing.

Nilai random_state dapat dipilih berapa saja, jika ingin memperoleh hasil yang persis sama dengan contoh ini maka gunakan 100. n_jobs dapat diisi maksimal sebanyak jumlah prosesor pada perangkat yang digunakan.

# Manajemen DataFrame
import pandas as pd
# Menghitung permutation importance
from sklearn.inspection import permutation_importance

# Menghitung Permutation Importance (100 ulangan)
pimp = permutation_importance(
    model_gb, X_test, y_test, n_repeats=100, random_state=100, n_jobs=4
)

result = pd.DataFrame(pimp["importances"], index=X.columns).T

# Menampilkan hasil untuk 5 kolom pertama
print(result.iloc[:,:5])

mean_result = result.mean(axis=0).sort_values(ascending=False)
print("\nNilai rata-rata Permutation Importance:\n")
print(mean_result)

OUTPUT    

     alcohol  malic_acid  ash  alcalinity_of_ash  magnesium
0   0.166667         0.0  0.0                0.0   0.074074
1   0.129630         0.0  0.0                0.0   0.037037
2   0.148148         0.0  0.0                0.0   0.055556
3   0.148148         0.0  0.0                0.0   0.055556
4   0.111111         0.0  0.0                0.0   0.074074
..       ...         ...  ...                ...        ...
95  0.074074         0.0  0.0                0.0   0.055556
96  0.111111         0.0  0.0                0.0   0.037037
97  0.185185         0.0  0.0                0.0   0.055556
98  0.203704         0.0  0.0                0.0   0.074074
99  0.074074         0.0  0.0                0.0   0.055556

[100 rows x 5 columns]

Nilai rata-rata Permutation Importance:

flavanoids                      0.244259
alcohol                         0.128889
color_intensity                 0.126296
proline                         0.098333
magnesium                       0.056852
od280/od315_of_diluted_wines    0.028889
malic_acid                      0.000000
ash                             0.000000
alcalinity_of_ash               0.000000
total_phenols                   0.000000
nonflavanoid_phenols            0.000000
proanthocyanins                 0.000000
hue                             0.000000
dtype: float64

Output yang ditampilkan di atas terdiri dari 2 bagian. Bagian pertama kita menampilkan contoh hasil permutation importance dari 5 peubah (alcohol, malic_acid, dst). Nilai yang ditampilkan pada setiap baris menunjukkan nilai permutation importance untuk ulangan pertama (indeks ke-0) hingga ke-100 (indeks ke-99).

Pada bagian kedua, kita tampilkan nilai rata-rata permutation importance berdasarkan nilai 100 ulangan. Hasil penghitungan menunjukkan bahwa peubah flavanoids merupakan peubah paling penting dari model. Ketika nilai pada peubah ini kita acak, maka secara rata-rata performa model akan berkurang hingga 0.244. Peubah penting berikutnya adalah alcohol dan color_intensity dengan nilai yang hampir sama.

Terdapat 7 peubah dengan rata-rata nilai 0, ini menunjukkan peubah-peubah tersebut tidak memberikan pengaruh apa-apa terhadap performa model. Namun sekali lagi, mungkin perlu pengecekan terlebih dahulu terhadap kemungkinan adanya kondisi multikolinieritas.

Karena penghitungan nilai dilakukan sebanyak 100 ulangan, maka selain nilai rataan, tentu kita dapat juga menghitung standar deviasinya sehingga dapat diukur pula selang bagi nilai permutation importance.

Nilai permutation importance sering kali dipresentasikan dalam bentuk boxplot. Berikut ini adalah visualisasi hasil yang sudah diperoleh pada bagian sebelumnya.

Python

# Visualisasi
import seaborn as sns
import matplotlib.pyplot as plt

sorted_index = result.mean(axis=0).sort_values(ascending=False).index
sorted_result = result[sorted_index]

plt.figure(figsize=(5, 6))
sns.boxplot(data=sorted_result, orient='h', 
            color='orange', linewidth=0.5, width=0.5,
            fliersize=1.5, flierprops={"marker": "o"})

plt.title("Permutation Importances (Data Test)")

Output

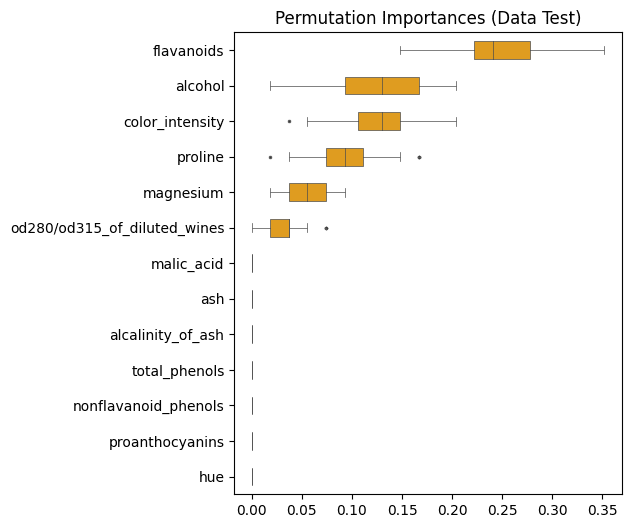
Melalui visualisasi boxplot seperti di atas, semakin memudahkan kita untuk memahami bagaimana posisi nilai permutation importance masing-masing peubah dalam mempengaruhi performa model.

Altmann, A., Toloşi, L., Sander, O., & Lengauer, T. (2010). Permutation importance: A corrected feature importance measure. Bioinformatics, 26(10), 1340–1347. https://doi.org/10.1093/BIOINFORMATICS/BTQ134

Drobnič, F., Kos, A., & Pustišek, M. (2020). On the Interpretability of Machine Learning Models and Experimental Feature Selection in Case of Multicollinear Data. Electronics 2020, Vol. 9, Page 761, 9(5), 761. https://doi.org/10.3390/ELECTRONICS9050761

• Python : Random Forest untuk Model Klasifikasi Menggunakan Scikit-Learn
• Tuning Hyperparameter Model Random Forest dengan Bahasa R
• Pemodelan Klasifikasi dengan Algoritma KNN (Prediksi Penderita Diabetes)
• Model Regresi Logistik untuk Klasifikasi Biner (Implementasi dengan R dan Python)
• Model Neural Network pada R Menggunakan Library Keras