Model Regresi Linier LASSO menggunakan Scikit-Learn


Least Absolute Shrinkage and Selection Operator (LASSO) atau juga disebut Regularisasi L1 merupakan salah satu bentuk regularisasi peubah. Selain itu, LASSO juga berfungsi sebagai operator seleksi peubah. Koefisien regresi LASSO diperoleh dengan meminimumkan nilai Residual Sum of Squares (RSS) pada model regresi (OLS) yang ditambahkan kendala $\lambda \sum{|\beta_j|}$.
Besaran penalti dikontrol melalui koefisien $\lambda$. Semakin besar nilai $\lambda$, maka nilai koefisien regresi akan semakin mendekati 0 bahkan bisa tepat sama dengan 0. Dengan penyusutan nilai koefisien menjadi 0 maka LASSO berfungsi sebagai seleksi peubah sehingga dapat menghasilkan model yang lebih sederhana dan lebih mudah diinteepretasikan. Selain itu, sangat penting untuk menentukan nilai $\lambda$ yang tepat untuk memperoleh model yang optimal.


Pada tulisan ini, kita akan membangun model Regresi LASSO menggunakan library scikit-learn pada bahasa pemrograman python. Selain itu, juga akan membandingkan hasilnya dengan model regresi linier (tanpa regularisasi) dan melakukan tuning hyperparameter.
Penyiapan Data
Dataset yang akan digunakan pada pembuatan model LASSO merupakan data simulasi dan dapat di-download pada link berikut:
Python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
data = pd.read_csv("data_simulasi.csv")
print(data.info())Output
<class 'pandas.core.frame.DataFrame'> RangeIndex: 10000 entries, 0 to 9999 Data columns (total 11 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 X1 10000 non-null float64 1 X2 10000 non-null float64 2 X3 10000 non-null float64 3 X4 10000 non-null float64 4 X5 10000 non-null float64 5 X6 10000 non-null float64 6 X7 10000 non-null float64 7 X8 10000 non-null float64 8 X9 10000 non-null float64 9 X10 10000 non-null float64 10 Y 10000 non-null float64 dtypes: float64(11) memory usage: 859.5 KB
Dataset terdiri dari 10 peubah bebas yaitu X1, X2 sampai X10 dengan semua data bertipe numerik. Adapun peubah Y sebagai peubah respon juga bertipe numerik. Total observasi dalam dataset adalah sebanyak 10.000.
Python
# Menghitung nilai korelasi corr = data.corr() mask = np.triu(np.ones_like(corr, dtype=bool)) cmap = sns.diverging_palette(230, 20, as_cmap=True) sns.heatmap(corr, mask=mask, cmap=cmap, vmax=1, center=0, linewidths=.1)
Output
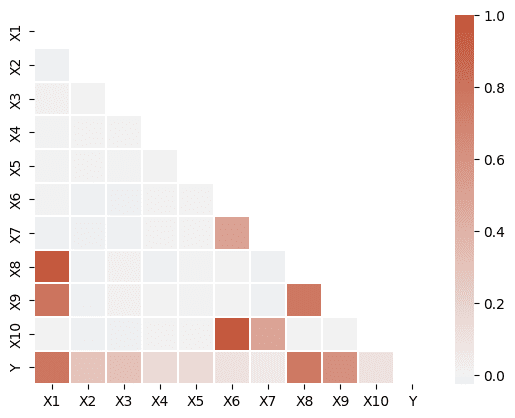
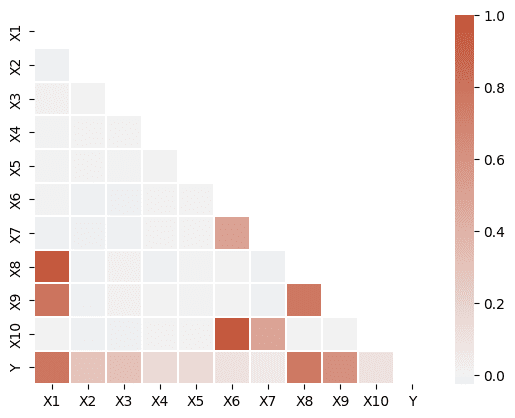
Pada dataset yang digunakan, terdapat beberapa peubah yang memiliki korelasi tinggi, seperti X1 dengan X8 dan X9, x6 dan X10, X8 dan X9. Dimana, dalam regresi linier, khususnya untuk inferensia, kemungkinan terdapat problem multikolinearitas pada model. Sehingga signifikansi peubah menjadi kurang reliabel untuk digunakan.
Namun fokus kita adalah bagaimana membentuk model prediksi terbaik, sehingga kita tidak akan melakukan pengecekan terlalu jauh untuk kondisi tersebut. Secara umum kondisi multikolinearitas juga tidak begitu mempengaruhi performa model dalam memprediksi.
Untuk hubungan masing-masing peubah X dengan peubah Y juga tampak bervariasi, seperti X1, X8, dan X9 memiliki korelasi yang cukup besar dengan peubah Y, sementara beberapa lainnya relatif kecil.
Pembagian Data dan Features Scaling
Proses splitting data menjadi data training dan testing penting dilakukan dalam pemodelan machine learning. Data training akan digunakan sebagai dasar pembentukan model. Adapun evaluasi model dilakukan berdasarkan data testing. Pengujian model dengan data yang berbeda agar evaluasi menjadi lebih “fair” dan mengurangi kemungkinan model overfitting.
Untuk proses splitting dapat menggunakan fungsi train_test_split dari modul sklearn.model_selection. Pada contoh ini kita menggunakan proporsi 70% sebagai data training dan 30% data testing.
Selanjutnya kita juga perlu melakukan features scaling. Dalam hal ini kita akan menggunakan fungsi StandardScaler dari modul sklearn.preprocessing. Fungsi ini akan membuat setiap fitur memiliki rataan 0 dan standar deviasi 1. Dengan begitu, skala dan rentang nilai pada semua fitur relatif sama.
Dengan data yang sudah terstandardisasi, nilai koefisien pada model secara mutlak menunjukkan besar kecilnya kontribusi fitur tersebut terhadap peubah responnya. Semakin besar nilai koefisien maka semakin besar kontribusinya terhadap nilai peubah respon dan begitu pula sebaliknya.
Python
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X = data.drop("Y", axis=1)
y = data["Y"]
# membagi data training dan testing
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=100)
# feature scaling
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.fit_transform(X_test)Model Regresi Linear
Model pertama yang akan dibuat adalah model regresi linear (OLS) tanpa regularisasi. Fungsi pada sklearn yang dipakai adalah fungsi LinearRegression dari modul sklearn.linear_model.
Setelah model terbentuk, langkah berikutnya adalah mengeevaluasi model. Terdapat banyak metrik yang dapat digunakan untuk mengukur performa model regresi. Di sini kita akan menggunakan Root Mean Square Error (RMSE) atau akar dari MSE. Jika diinginkan, kita dapat menghitung nilai MSE secara manual dengan membandingkan nilai prediksi terhadap nilai yang sebenarnya. Namun pada sklearn terdapat fungsi mean_squared_error yang dapat kita gunakan langsung.
Dari hasil di atas diperoleh RMSE untuk model regresi linier adalah sebesar 10,0315.
Kemudian, untuk melihat koefisien dari masing-masing peubah dapat mengakses properti coef_.
Berdasarkan nilai koefisien regresi di atas, dapat dinyatakan bahwa X1 memiliki kontribusi paling besar dibandingkan peubah lainnya terhadap nilai peubah respon (Y).
Python
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
model_reg = LinearRegression()
# Fitting model
model_reg.fit(X_train, y_train)
# Prediksi data testing
y_pred_reg = model_reg.predict(X_test)
# menghitung RMSE model regresi pada data testing
rmse_reg = mean_squared_error(y_test, y_pred_reg)**0.5
menampilkan nilai RMSE
print("RMSE (Testing):", rmse_reg)
# menampilkan koefisien regresi
print(model_reg.coef_)Output
RMSE (Testing): 10.031543304211139
# (Koef X1 - X10)
array([20.74785254, 8.0149942 , 7.84860767, 3.97249809, 3.81190903,
3.06322583, 0.32076385, -0.48497973, 0.11595971, -0.26297624])Regresi Lasso
Untuk membuat model regresi LASSO kita menggunakan fungsi Lasso dari modul sklearn.linear_model. Pada fungsi Lasso, konstanta lambda ditentukan melalui parameter alpha.
Python
from sklearn.linear_model import Lasso
# Model LASSO dengan alpha=1
model_lasso = Lasso(alpha=1)
# Fitting model LASSO
model_lasso.fit(X_train, y_train)
# prediksi data testing
y_pred_lasso = model_lasso.predict(X_test)
# menghitung RMSE model LASSO pada data testing
rmse_lasso = mean_squared_error(y_test, y_pred_lasso)**0.5
print("RMSE (Testing):", rmse_lasso)
print("Koefisien :")
print(model_lasso.coef_)Output
# Output RMSE (Testing): 10.312108520556315 Koefisien : [19.33283097 6.99131085 6.84358933 2.97497882 2.83637252 1.92993902 0. 0. 0. 0. ]
Seperti yang sudah disampaikan di awal, regularisasi L1 atau Lasso juga berfungsi untuk seleksi peubah. Dengan nilai alpha yang memadai, koefisien regresi dari peubah yang tidak begitu berpengaruh terhadap model dapat disusutkan hingga tepat bernilai 0. Hal ini tentu akan membuat model menjadi lebih sederhana.
Model dengan nilai alpha=1 membuat koefisien dari X7, X8, X9 dan X10 berilai 0. Nilai RMSE model ini memang lebih tinggi yaitu 10.3121, namun model yang diperoleh jauh lebih sederhana karena hanya menggunakan 6 variabel saja.
Tuning Hyperparameter
Pada model LASSO sebelumnya, kita menentukan nilai alpha sebesar 1. Nilai alpha yang optimal dapat kita cari melalui tuning hyperparameter menggunakan validasi silang (cross validation). Pada skelarn, fungsi yang digunakan adalah LassoCV.
Pertama, tentukan daftar nilai alpha yang akan dicobakan pada model. Selanjutnya, dengan menggunakan fungsi LassoCV kita buat model dengan parameter alphas berupa list_alpha yang sudah dibuat sebelumnya.
Parameter cv merupakan jumlah fold yang digunakan dalam proses validasi silang. Nilai yang umum adalah 5 atau 10 (default). Penentuan model terbaik di sini adalah berdasarkan hasil validasi silang pada data training. Hasil evaluasi model menggunakan data uji tidak menutup kemungkinan tidak sebaik pada data training. Namun jika model tidak overfitting, maka nilai yang diperoleh tidak akan begitu jauh berbeda.
Python
from sklearn.linear_model import LassoCV
list_alpha = [0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 0.75, 0.9, 0.99]
model_lasso_cv = LassoCV(alphas=list_alpha, cv=5)
# Fitting model Lasso CV
model_lasso_cv.fit(X_train, y_train)
# Prediksi data testing
y_pred_lasso_cv = model_lasso_cv.predict(X_test)
# Menghitung RMSE pada data testing
rmse_lasso_cv = mean_squared_error(y_test, y_pred_lasso_cv)**0.5
# Nilai alpha pada model terbaik
print("alpha:", model_lasso_cv.alpha_)
print("RMSE (Testing):", rmse_lasso_cv)
print("Koefisien:")
print(model_lasso_cv.coef_)Output
# Output alpha: 0.02 RMSE (Testing): 10.030604720206197 Koefisien: [20.25675928 7.99464087 7.82996735 3.95321927 3.79338291 2.78927852 0.30872243 0. 0.10708265 0. ]
Model Regresi LASSO hasil validasi silang menunjukkan bahwa nilai alpha optimal adalah 0,02. Adapun hasil evaluasi pada data testing menunjukkan nilai RMSE 10,0306. Nilai ini lebih baik dibandingkan model regresi linier biasa maupun pada model LASSO dengan alpha=1.
Adapu koefisien untuk X8 dan X10 bernilai 0. Artinya model ini lebih sederhana dibandingkan model linier biasa dan juga memiliki performa yang relatif lebih baik.
Referensi
- James, G., Witten, D., Hastie, T., Tibshirani, R. 2014, An Introduction to Statistical Learning with Applications in R, Springer.
- Lasso (Scikit-Learn): sklearn.linear_model.Lasso
- LassoCV (Scikit-Learn): sklearn.linear_model.LassoCV








