Pengenalan Algoritma Clustering DBSCAN

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) merupakan salah satu algoritma clustering yang paling banyak digunakan dalam data science dan machine learning karena kemampuannya dalam mengidentifikasi pola kelompok data berdasarkan kepadatan lokal, serta kemampuannya menangani outlier secara eksplisit. Berbeda dengan metode clustering seperti K-means yang mengharuskan pengguna untuk menetapkan jumlah cluster di awal dan hanya efektif untuk struktur data berbentuk bulat atau homogen, DBSCAN menawarkan fleksibilitas untuk mengenali cluster dengan bentuk arbitrer dan kepadatan yang beragam.

DBSCAN sangat relevan dalam berbagai domain aplikasi, seperti deteksi intrusi pada sistem keamanan siber, pengelompokan pelanggan berdasarkan perilaku konsumsi, identifikasi zona geografis berdasarkan data spasial, termasuk juga sebagai alat deteksi outlier pada data multivatriat. Keunggulan utama algoritma ini adalah kemampuannya untuk menyusun kelompok berdasarkan distribusi spasial tanpa harus memaksakan batas geometris yang kaku.

Pada tulisan ini kita akan membahas prinsip kerja DBSCAN dari sisi konseptual dan matematis, serta bagaimana pendekatan berbasis kepadatan ini bekerja secara iteratif dan efektif dalam memetakan pola tersembunyi dalam data multivariat.

Berikut adalah beberapa keunggulan algoritma DBSCAN:

• Tidak memerlukan jumlah cluster sebagai input
• Fleksibel terhadap bentuk cluster sehingga dapat mengenali bentuk tidak reguler
• Robust terhadap outlier: Noise tidak dimasukkan dalam cluster
• Stabil terhadap transformasi data: Tidak terpengaruh rotasi, translasi, atau skala (dengan asumsi jarak dinormalisasi)
• Tidak sensitif terhadap inisialisasi: Berbeda dengan K-means yang bisa memberikan hasil berbeda tergantung titik awal

Meskipun demikian, terdapat beberapa keterbatasan yang perlu menjadi perhatian ketika menggunakan algoritma ini, yaitu:

• Curse of dimensionality: Dalam dimensi tinggi, semua titik cenderung memiliki jarak serupa sehingga sulit menentukan ε yang optimal
• Sensitivitas terhadap parameter: Pemilihan ε dan minPts sangat mempengaruhi hasil
• Tidak cocok untuk data dengan kepadatan bervariasi: Sulit membedakan cluster longgar dari noise
• Skalabilitas terbatas: Pada dataset besar, performa menurun tanpa penggunaan struktur data efisien (misal KD-Tree)

Dasar pemikiran DBSCAN adalah bahwa cluster merupakan area-area dengan konsentrasi titik data yang tinggi, dipisahkan oleh wilayah yang memiliki kepadatan rendah. Dalam kerangka ini, sebuah cluster dibentuk oleh titik-titik yang cukup dekat secara spasial dan cukup padat berdasarkan kriteria lokal.

Untuk mengukur kedekatan dan kepadatan ini, dua parameter utama diperkenalkan:

• ε (epsilon): radius atau jarak maksimum untuk mengidentifikasi tetangga dari suatu titik.
• minPts: jumlah minimum titik dalam radius ε agar titik pusat dapat dikategorikan sebagai titik inti (core point).

Berdasarkan kedua parameter tersebut, setiap titik dikategorikan menjadi tiga jenis:

1. Core point: Titik-titik di mana memiliki setidaknya minPts tetangga dalam radius ε. Titik ini berada di area yang padat dan menjadi pusat pembentukan cluster.
2. Border point: Titik yang berada dalam radius ε dari core point tetapi tidak memiliki cukup tetangga untuk menjadi core point sendiri.
3. Noise point: Titik yang tidak masuk dalam cluster manapun, biasanya tersebar secara acak atau jauh dari kepadatan lokal — sering disebut outlier.

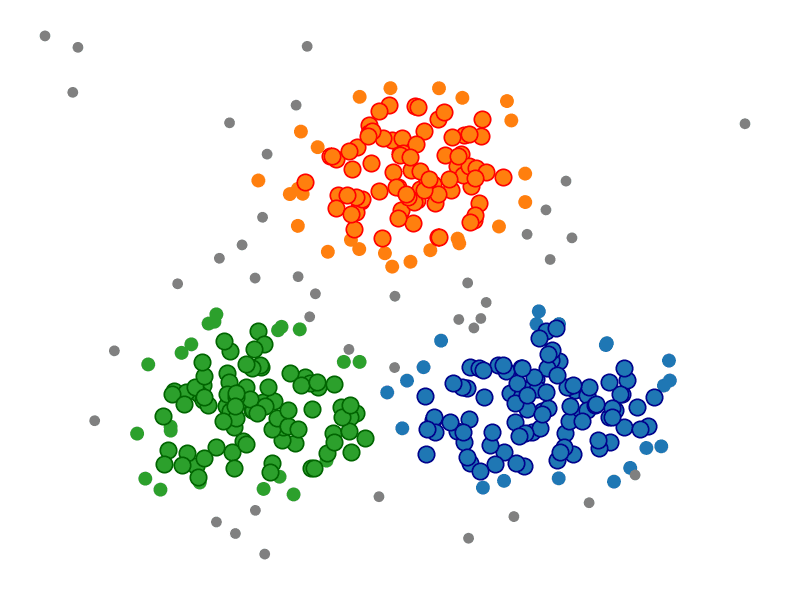
Gambar 1 memberikan ilustrasi bagaimana hasil cluster menggunakan DBSCAN dengan epsilon dan minPts tertentu. Dari gambar tersebut, titik-titik yang paling besar merupakan titik-titik core point, di mana dalam radius epsilon dari titik tersebut mencakup setidaknya minPts titik. Sementara itu, titik-titik berwarna orange, hijau dan biru yang lebih kecil merupakan border point. Dan untuk titik berwarna abu-abu merupakan noise point atau dapat dikatakan outlier karena berada diluar kepadatan lokal titik-titik lainnya.

Untuk mendefinisikan proses clustering DBSCAN secara matematis, kita mulai dengan menyatakan himpunan data berdimensi (d):

$$
D = {x_1, x_2, \ldots, x_n} \subset \mathbb{R}^d
$$

• ε-neighborhood: ε-neighborhood dari titik ($x_i$) adalah himpunan semua titik dalam jarak maksimum ($\epsilon$) terhadap titik tersebut: $$
  N_\epsilon(x_i) = {x_j \in D \mid \text{dist}(x_i, x_j) \leq \epsilon}
  $$ Fungsi jarak yang umum digunakan adalah jarak Euclidean: $$
  \text{dist}(x_i, x_j) = \sqrt{ \sum_{k=1}^d (x_{ik} – x_{jk})^2 }
  $$
• Core Point: Titik ($x_i$) dikatakan sebagai core point apabila jumlah titik dalam ε-neighborhood-nya minimal sebanyak minPts: $$
  |N_\epsilon(x_i)| \geq \text{minPts}
  $$
• Directly Density-Reachable: Titik ($x_j$) disebut directly density-reachable dari titik ($x_i$) apabila: $$
  x_j \in N_\epsilon(x_i) \quad \text{dan} \quad x_i \text{ adalah core point}
  $$
• Density-Reachable: Titik ($x_j$) density-reachable dari ($x_i$) jika terdapat rangkaian titik: $$
  x_i = x_1, x_2, \ldots, x_k = x_j
  $$ sedemikian sehingga: $$
  x_{l+1} \in N_\epsilon(x_l) \quad \text{dan} \quad x_l \text{ adalah core point}, \quad \forall l = 1, \ldots, k-1
  $$
• Density-Connected: Dua titik ($x_a$) dan ($x_b$) dikatakan density-connected jika terdapat titik core ($x_c$) sehingga keduanya density-reachable dari titik tersebut: $$
  x_a \text{ dan } x_b \text{ keduanya density-reachable dari } x_c
  $$
• Definisi Cluster: Suatu cluster didefinisikan sebagai himpunan maksimal dari titik-titik yang saling density-connected: $$
  C \subset D, \quad \forall x_i, x_j \in C, \quad x_i \text{ density-connected dengan } x_j
  $$

Secara umum proses pembentukan cluster pada algoritma DBSCAN adalah sebagai berikut:

1. Untuk setiap titik dalam dataset, hitung jumlah tetangga dalam radius epsilon.
2. Tandai titik tersebut sebagai core point jika jumlah titiknya (termasuk titik itu sendiri) ≥ minPts.
3. Jika titik adalah core, mulai bentuk cluster baru dan tambahkan semua titik yang density-reachable dari titik tersebut.
4. Lanjutkan iterasi ke titik berikutnya yang belum diklasifikasikan.
5. Titik yang tidak pernah ditambahkan ke cluster manapun dianggap sebagai noise.

Proses ini berakhir ketika seluruh titik telah dikunjungi. Karakteristik menarik dari DBSCAN adalah bahwa hasil clustering tidak tergantung pada urutan pemeriksaan titik, menjadikannya deterministik jika parameter tetap.

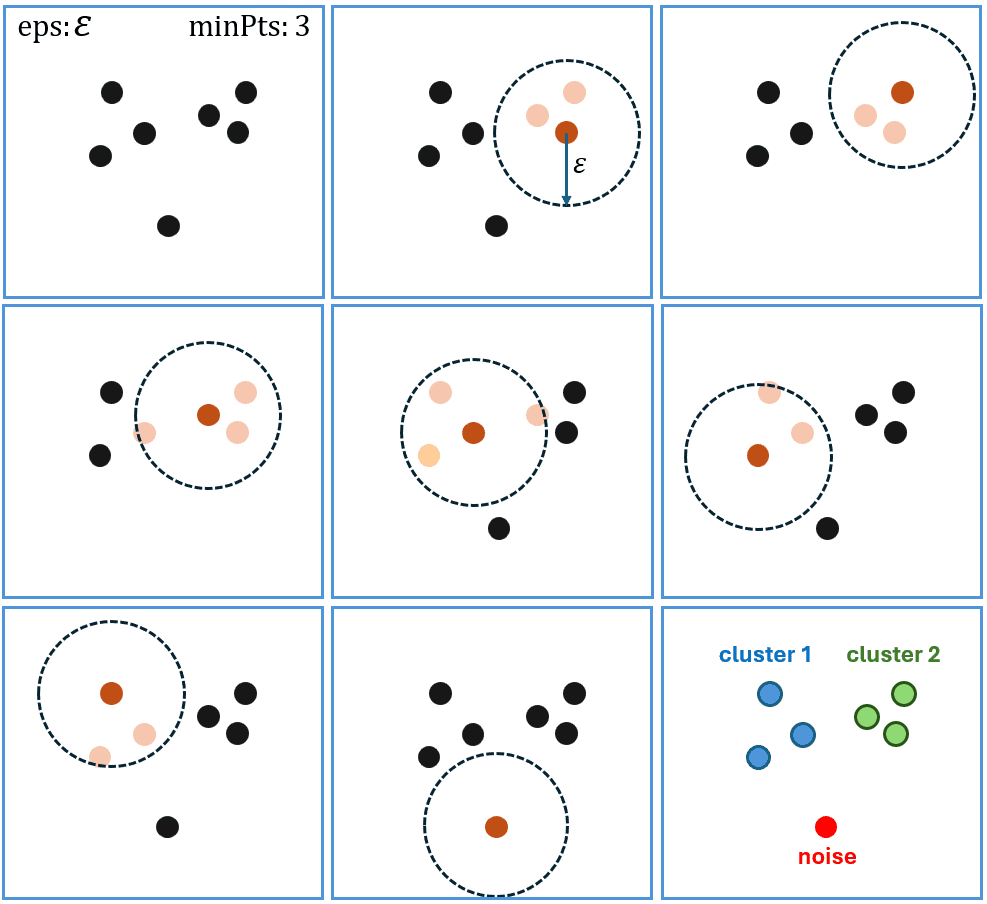
Ilustrasi pada Gambar 2 menyajikan contoh sederhana bagaimana data dikelompokkan dengan algoritma DBSCAN. Tentu saja aliran yang disajikan sudah disimplifikasi. namun tetap memberikan gambaran yang cukup jelas. Pada contoh ini misalnya parameter yang digunakan adalah epsilon $\epsilon$ dan minPts 3.

Pemilihan nilai parameter epsilon dan minPts sangat menentukan hasil clustering DBSCAN. Kombinasi nilai yang tidak tepat dapat menyebabkan banyaknya data yang dikategorikan sebagai noise, atau sebaliknya, menghasilkan cluster yang terlalu luas dan tidak bermakna.

Secara umum:

• Nilai epsilon yang terlalu kecil menyebabkan sebagian besar titik tidak memiliki cukup tetangga dan dianggap sebagai outlier.
• Nilai epsilon yang terlalu besar berisiko menggabungkan beberapa cluster yang seharusnya terpisah.
• Nilai minPts yang terlalu rendah membuat DBSCAN terlalu sensitif terhadap noise, sedangkan nilai yang terlalu tinggi bisa membuat cluster sulit terbentuk.

Dengan demikian, penentuan nilai-nilai yang tepat sangat penting untuk mendapatkan hasil clustering yang baik. Terdapat beberapa pendekatan yang dapat digunakan untuk menentukan nilai parameter secara lebih sistematis, antara lain:

• K-Distance Plot: Menghitung jarak ke tetangga ke-minPts terdekat untuk setiap titik, kemudian mengurutkannya dan memvisualisasikan dalam grafik. Titik “tekukan” pada grafik tersebut dianggap sebagai kandidat nilai epsilon yang optimal.
• Grid Search / cross validation (jika tersedia label evaluasi):
  Jika tersedia metrik eksternal seperti silhouette score, atau sebagian label data, maka kedua aprameter dapat ditentukan dengan menguji kombinasi nilai secara sistematis.
• Berbasis domain knowledge:
  Dalam kasus spasial, epsilon dapat dikaitkan dengan jarak yang sebenarnya (misalnya dalam meter atau kilometer) yang bermakna dalam konteks aplikasi tertentu.

Dengan pendekatan yang tepat, proses penyesuaian parameter ini dapat membantu menghasilkan hasil clustering DBSCAN yang lebih valid, stabil, dan sesuai dengan struktur alami data.

• Aggarwal, C. C., & Reddy, C. K. (2014). Data Clustering: Algorithms and Applications. CRC Press.
• Ester, M., Kriegel, H. P., Sander, J., & Xu, X. (1996). A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), 226–231.
• Schubert, E., Sander, J., Ester, M., Kriegel, H. P., & Xu, X. (2017). DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Transactions on Database Systems (TODS), 42(3), 19.
• Han, J., Kamber, M., & Pei, J. (2011). Data Mining: Concepts and Techniques (3rd ed.). Elsevier.

• K-Means Clustering dengan Python
• Hierarchical Clustering: Agglomerative Cluster dengan Python
• Principal Component Analysis (PCA) dengan R