Bayesian Optimization: Teori dan Intuisi


Tuning hyperparameter adalah langkah krusial dalam pengembangan model machine learning. Penentuan hyperparameter yang tepat dapat meningkatkan performa model secara signifikan, sebaliknya pemilihan yang kurang tepat dapat mengurangi akurasi prediksi. Metode konvensional seperti grid search dan random search sering digunakan untuk mencari kombinasi hyperparameter terbaik karena kemudahannya, namun metode ini bisa sangat memakan waktu dan sumber daya, terutama ketika berhadapan dengan ruang hyperparameter yang besar dan kompleks.
Di sinilah Bayesian Optimization menjadi pilihan yang lebih efektif dan efisien. Berangkat dari teori probabilitas dan statistik, Bayesian Optimization dapat mengeksplorasi dan mengeksploitasi ruang hyperparameter secara lebih efesien, membantu menemukan kombinasi optimal dengan lebih sedikit percobaan. Inti dari Bayesian Optimization adalah pendekatan berbasis model untuk mengarahkan pencarian ke arah yang lebih menjanjikan dengan memanfaatkan model probabilistik. Algoritma ini bekerja dengan membangun model probabilistik (model surrogate) dari fungsi objektif yang ingin dioptimalkan, kemudian menggunakan model tersebut untuk memilih titik evaluasi berikutnya yang dianggap paling menjanjikan.
Model Surrogate
Model surrogate adalah model statistik yang digunakan untuk memperkirakan fungsi objektif yang sebenarnya. Karena evaluasi langsung pada setiap titik dari fungsi objektif sering kali sangat mahal secara komputasi, model surrogate ini digunakan untuk memprediksi nilai fungsi pada titik-titik yang belum dievaluasi. Dengan demikian memungkinkan pencarian hyperparameter yang lebih efisien.
Model surrogate yang paling umum digunakan dalam Bayesian Optimization adalah Gaussian Process (GP). GP merupakan model non-parametrik yang mendefinisikan distribusi probabilistik atas fungsi objektif. Keunggulan utama GP adalah kemampuannya untuk memberikan tidak hanya prediksi nilai fungsi tetapi juga selang kepercayaan dari prediksi tersebut.
Berikut ini adalah karakteristik dari GP:
Distribusi Prior
GP memulai dengan asumsi awal tentang fungsi objektif, yang disebut distribusi prior. Prior ini biasanya diambil sebagai distribusi Gaussian dengan mean $\mu(x)$ dan covariance yang ditentukan oleh kernel $k(x, x’)$.
$f(x) \sim \mathcal{GP}(\mu(x), k(x, x’))$
Kernel (Fungsi Covariance)
Kernel adalah komponen esensial dari GP yang mendefinisikan hubungan antara titik-titik dalam ruang hyperparameter dan mengontrol bagaimana GP memodelkan korelasi antara pasangan titik data. Oleh karena itu, kernel memainkan peran penting dalam menentukan karakteristik dari model GP.
Dalam praktiknya, kernel yang umum digunakan adalah Exponential Quadratic (EQ):
$k(x, x’) = \sigma_f^2 \exp \left( -\frac{1}{2l^2} \| x – x’ \|^2 \right)$
di mana $\sigma_f^2$ adalah variance dan $l$ adalah panjang skala.
Selain kernel EQ, terdapat kernel lainnya seperti White Noise, Matern, Rational Quadratic, Periodic dan sebagainya.
Distribusi Posterior
Setelah data observasi baru ditambahkan, GP memperbarui distribusi menjadi distribusi posterior. Distribusi ini menggabungkan prior dengan informasi baru, menghasilkan prediksi yang lebih akurat dan dengan ketidakpastian yang lebih rendah di sekitar titik-titik yang telah diamati.
Misalkan terdapat data observasi $D = \{ (x_i, y_i) \}_{i=1}^n$, di mana $x_i$ adalah hyperparameter dan $y_i$ adalah nilai fungsi objektif. Distribusi posterior dari GP dapat dinyatakan sebagai:
$p(f | D, x) = \mathcal{GP}(\mu_n(x), k_n(x, x’))$
dengan mean dan covariance yang diperbarui sebagai:
$\mu_n(x) = k(x, X) [K(X, X) + \sigma_n^2 I]^{-1} y$
$k_n(x, x’) = k(x, x’) – k(x, X) [K(X, X) + \sigma_n^2 I]^{-1} k(X, x’)$
di mana $k(x, X)$ adalah vektor covariance antara $x$ dan semua titik dalam $X$, $K(X, X)$ adalah matriks covariance antara semua pasangan titik dalam $X$, dan $\sigma_n^2$ adalah noise variance.
Fungsi Akuisisi
Fungsi akuisisi adalah komponen penting dalam Bayesian Optimization dalam menentukan titik baru dalam ruang hyperparameter yang akan dievaluasi. Hasil prediksi dari model surrogate menjadi dasar bagi fungsi akuisisi untuk menyeimbangkan eksplorasi (mencari di area dengan ketidakpastian tinggi) dan eksploitasi (mencari di area dengan nilai fungsi objektif yang diharapkan tinggi). Titik dengan nilai fungsi akuisisi tertinggi dipilih sebagai titik evaluasi berikutnya.
Jenis-Jenis Fungsi Akuisisi
Beberapa fungsi akuisisi yang umum digunakan dalam Bayesian Optimization adalah:
1. Expected Improvement (EI)
EI merupakan pilihan fungsi akuisisi yang paling umum digunakan dalam Bayesian Optimization. EI mengukur peningkatan nilai ekspektasi dari evaluasi pada titik $x$ dibandingkan dengan nilai terbaik yang telah ditemukan sejauh ini.
Persamaan fungsi EI didefinisikan sebagai:
$\alpha_{EI}(x) = \mathbb{E}[\max(0, f(x) – f(x^+))]$
di mana $f(x^+)$ adalah nilai terbaik yang telah ditemukan. Dalam kasus Gaussian Process, EI dapat diekspresikan secara tertutup sebagai:
$\alpha_{EI}(x) = ( \mu(x) – f(x^+) ) \Phi(Z) + \sigma(x) \phi(Z)$
dengan:
$Z = \begin{aligned}\frac{\mu(x) – f(x^+)}{\sigma(x)}\end{aligned}$
di mana $\mu(x)$ dan $\sigma(x)$ adalah mean dan standard deviation dari prediksi GP pada titik $x$, $\Phi$ adalah cumulative distribution function (CDF) dari distribusi normal standar, dan $\phi$ adalah probability density function (PDF) dari distribusi normal standar.
2. Probability of Improvement (PI)
Probability of Improvement (PI) mengukur probabilitas bahwa evaluasi pada titik $x$ akan menghasilkan perbaikan dibandingkan dengan nilai terbaik yang telah ditemukan. PI didefinisikan sebagai:
$\alpha_{PI}(x) = \mathbb{P}(f(x) > f(x^+))$
dalam kasus Gaussian Process, PI dapat diekspresikan sebagai:
$\begin{aligned}\alpha_{PI}(x) = \Phi \left( \frac{\mu(x) – f(x^+)}{\sigma(x)} \right)\end{aligned}$
di mana $\Phi$ adalah CDF dari distribusi normal standar.
3. Upper Confidence Bound (UCB)
Upper Confidence Bound (UCB) mengukur kombinasi dari mean dan ketidakpastian prediksi pada titik $x$. Fungsi ini dirancang untuk memberikan eksplorasi yang lebih agresif. UCB didefinisikan sebagai:
$\alpha_{UCB}(x) = \mu(x) + \kappa \sigma(x)$
di mana $\kappa$ adalah parameter yang mengontrol keseimbangan antara eksplorasi dan eksploitasi. Nilai $\kappa$ yang lebih besar mendorong eksplorasi lebih banyak.
4. Lower Confidence Bound (LWB)
Lower Confidence Bound (LCB) adalah kebalikan dari UCB dan sering digunakan untuk minimisasi fungsi objektif. LCB mengukur kombinasi dari mean dan ketidakpastian prediksi pada titik $x$. Fungsi ini juga dirancang untuk memberikan eksplorasi yang lebih agresif. LCB didefinisikan sebagai:
$\alpha_{LCB}(x) = \mu(x) – \kappa \sigma(x)$
di mana $\kappa$ adalah parameter yang mengontrol keseimbangan antara eksplorasi dan eksploitasi. Nilai $\kappa$ yang lebih besar mendorong eksplorasi lebih banyak.
Memilih Fungsi Akuisisi
Pemilihan fungsi akuisisi tergantung pada tujuan dan sifat masalah yang dihadapi:
- Expected Improvement (EI) cocok untuk situasi di mana kita ingin menyeimbangkan eksplorasi dan eksploitasi secara proporsional.
- Probability of Improvement (PI) lebih sederhana dan fokus pada eksploitasi, cocok untuk masalah dengan evaluasi yang lebih murah.
- Upper Confidence Bound (UCB) memberikan kontrol eksplorasi yang lebih eksplisit, cocok untuk masalah dengan ketidakpastian yang tinggi atau ketika eksplorasi yang lebih agresif diperlukan.
- Lower Confidence Bound (LCB) cocok untuk masalah minimisasi dan memberikan kontrol eksplorasi yang lebih eksplisit.
Ilustrasi Bayesian Optimization
Dalam dunia machine learning, terdapat banyak pustaka yang dapat digunakan untuk tugas Bayesian Optimization. Namun, untuk memahami secara baik proses kerja Bayesian Optimization, khususnya menggunakan Gaussian Proccess, maka pada bagian ini akan dibuat ilustrasi sederhana menggunakan Python. Setiap langkah utama akan kita definisikan secara manual disertai visualisasi yang membantu.
Catatan: Pada praktiknya, ketika berbicara pencarian titik optimal ataupun nilai $X$ dalam konteks tuning hyperparameter model, yang dimaksudkan adalah nilai-nilai hyperparameternya dan bukanlah fitur-fitur (peubah prediktor) pada dataset. Contohnya, pada model KNN, yang dimaksud dengan $X$ yaitu nilai $k$ atau jumlah tetangga. Pada model random forest, nilai $X$ dapat berupa jumlah pohon, kedalaman maksimal pohon, jumlah variabel, dan jumlah data minimal untuk proses split. Pada contoh lainnya yang lebih kompleks misalkan Neural Network, maka $X$ yang dimaksud dapat berupa kumpulan hyperparameter yang mencakup jumlah layer, jumlah neuron, fungsi aktivasi, learning rate, dan sebagainya.
Fungsi Objektif
Misal kita ingin mencari nilai optimum untuk suatu fungsi yang tidak diketahui. Tentu sebagai bagian dari ilustrasi dan karena hanya menggunakan 1 variabel, kita dapat memvisualisasikan fungsi objektif tersebut.
1. Tahapan Inisiasi
Fungsi yang ingin kita optimalkan adalah $sin(X)+sin(3X)+0.2X^2+0.1X$. Pada Gambar 1, fungsi objektif yaitu berupa kurva berwarna biru (fungsi ini tidak diketahui). Sebagai langkah awal dalam Bayesian Optimization, kita menggunakan model surrogate Gaussian Proccess. Seperti yang juga tersaji pada Gambar 1, garis putus-putus berwarna merah menunjukkan nilai tengah model untuk setiap titik x, dan area disekitarnya adalah selang kepercayaan 95%. Karena belum melakukan eksplorasi pada titik manapun, maka pada tahap inisial tentu saja fungsi ini hanya berupa garis lurus dengan nilai tengah 0 dan simpangan baku 1 untuk setiap titik x.
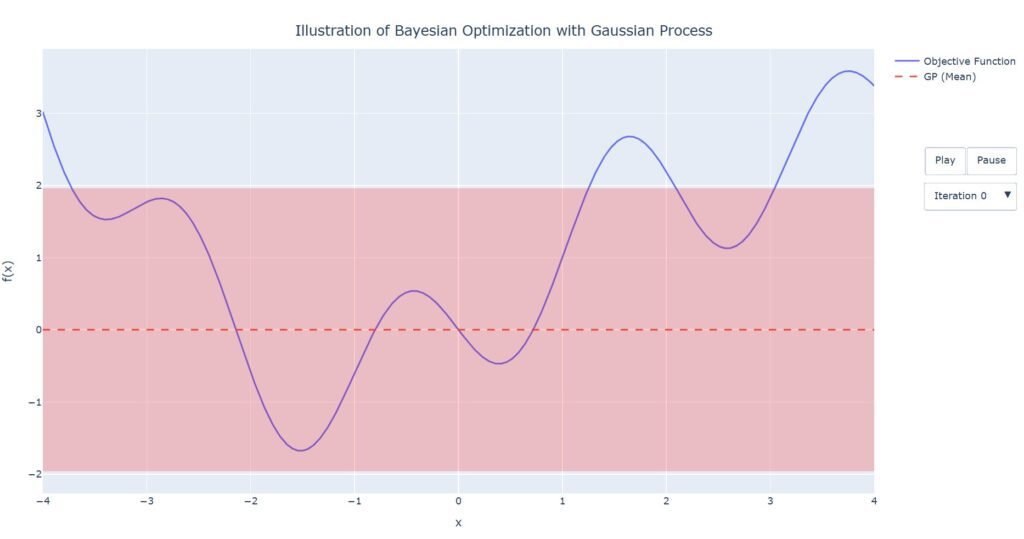

2. Iterasi Awal
Selanjutnya, pada iterasi awal, kita dapat mengevaluasi beberapa titik acak sekaligus, misalkan 2 titik (Pada contoh Gambar 2 kebetulan dua titik acak terpilih adalah berdekatan). Berdasarkan 2 titik ini selanjutnya dilakukan pembaruan model surrogate. Pada bagian ini fungsi kernel menentukan struktur dari covariance dari titik-titik pada terpilih dan berdasarkan hal tersebut, menentukan bentuk fungsi posterior-nya. Seperti terlihat pada Gambar 2, nilai tengah model sudah tidak konstan pada titik 0, melainkan membentuk kurva tertentu. Selang kepercayaan fungsi pada area disekitar titik juga menjadi lebih kecil, sementara selang kepercayaan pada daerah lainnya yang belum dieksplorasi tentunya masih sangat lebar.
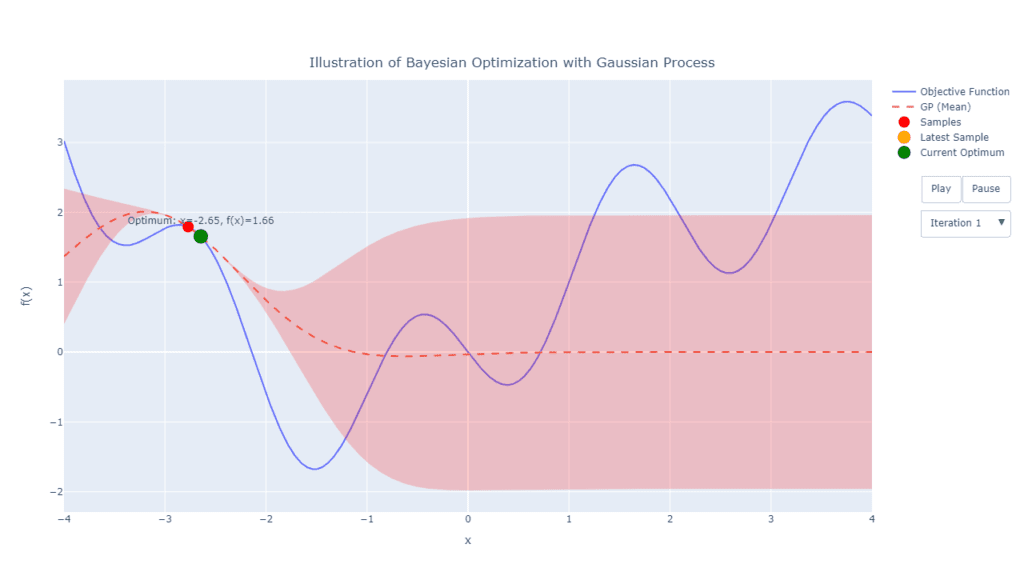

3. Pencarian Titik Baru
Setelah titik awal yang dipilih secara acak, titik berikutnya (misalnya titik ketiga) akan dipilih dengan mengoptimalkan fungsi EI menggunakan teknik seperti minimisasi atau optimasi numerik untuk menemukan lokasi yang diperkirakan paling menjanjikan untuk evaluasi berikutnya.
Sama seperti tahap sebelumnya, setelah ditentukan titik baru, maka model surrogate diperbarui kembali berdasarkan tambahan titik baru tersebut. Langkah ini dapat dilakukan secara iteratif berdasarkan kriteria yang sudah ditentukan.


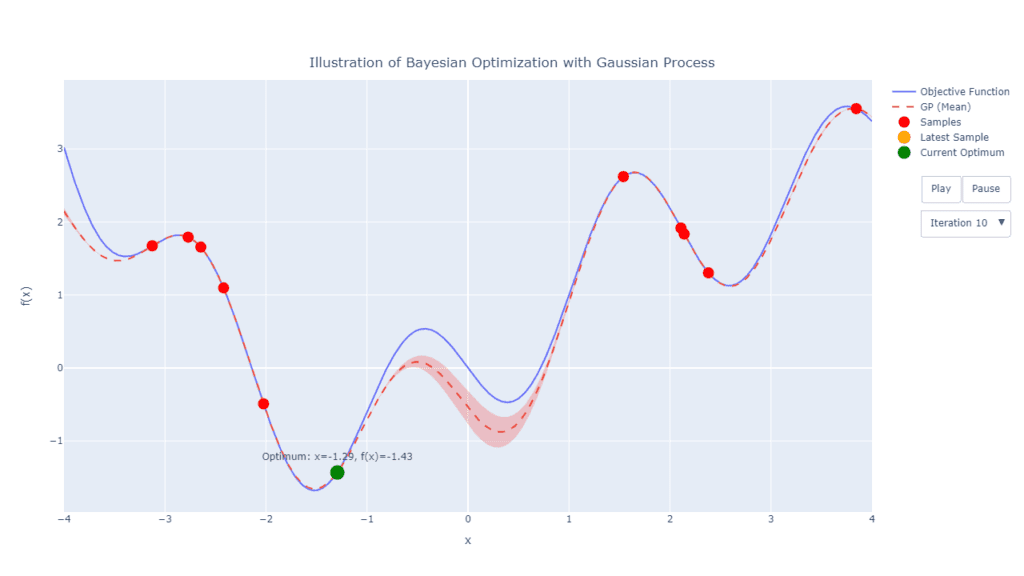

4. Pemberhentian Pencarian
Proses iterasi dalam Bayesian Optimization biasanya dihentikan berdasarkan salah satu dari beberapa kriteria berikut:
- Jumlah Iterasi Maksimal: Optimisasi berhenti setelah mencapai jumlah iterasi yang ditentukan sebelumnya.
- Konvergensi: Proses dihentikan jika solusi optimal sudah mendekati atau mencapai konvergensi, yang dapat diukur dengan nilai objektif atau kondisi lain yang ditetapkan.
- Kondisi Penghentian: Kondisi berhenti khusus seperti mencapai toleransi kesalahan tertentu atau tidak ada peningkatan yang signifikan dalam nilai objektif setelah beberapa iterasi.
- Waktu Komputasi: Dihentikan setelah melewati batas waktu komputasi yang ditetapkan.
- Kriteria Bisnis atau Praktis: Misalnya, berdasarkan hasil evaluasi atau kesesuaian dengan kebutuhan bisnis.
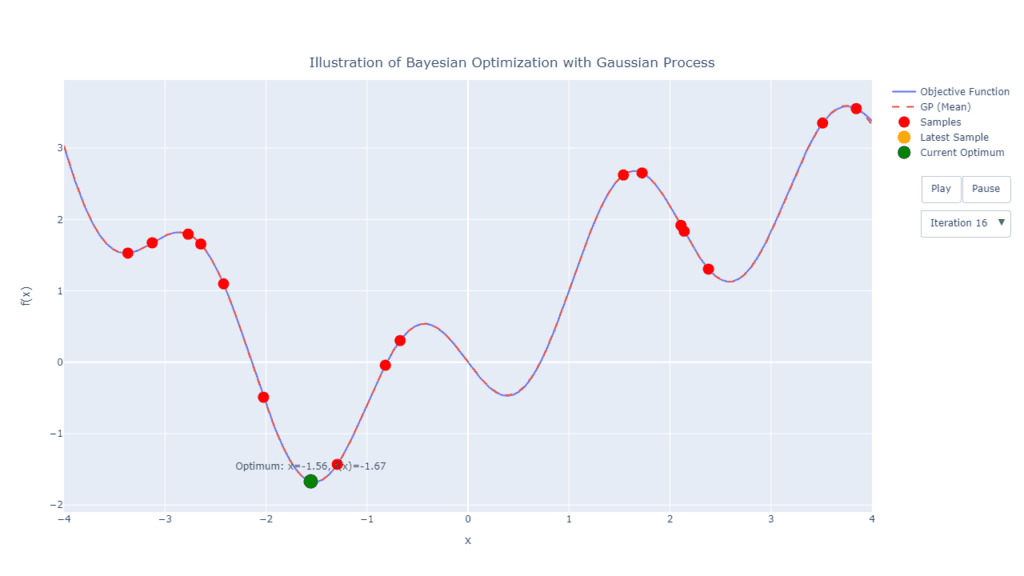

Pada Gambar 5 di atas, dapat dilihat bahwa pada iterasi ke-16 sudah dihasilkan nilai yang konvergen. Bahkan fungsi posterior yang diperoleh berdasarkan eksplorasi pada 17 titik saja sangat mendekati fungsi objektif aslinya. Namun perlu diingat, fungsi objektif pada contoh ini tentu sangat sederhana, dengan 1 peubah X saja (1 hyperparameter) sehingga dapat konvergen dengan begitu cepat.
Model machine learning umumnya memiliki algoritma yang rumit, jenis hyperparameter yang besar serta metrik kinerja yang beragam, tentu proses pencarian jauh lebih sulit dan mahal. Kita juga tidak bisa memastikan hasil yang diperoleh sudah merupakan hasil optimal global. Namun ilustrasi yang disajikan dapat memberikan bagaimana tahapan tersebut bekerja ketika kita melakukan tuning hyperparameter menggunakan Bayesian Optimization.
Sintaks Lengkap
Berikut sintaks program python lengkap ilustrasi yang disajikan sebelumnya. Kode juga tersedia pada github berikut: bayesian-optimization-ilustration.
Python
import numpy as np
from scipy.optimize import minimize
from scipy.spatial.distance import cdist
from scipy.stats import norm
import plotly.graph_objects as go
# Kernel Quadratic Exponential
def kernel_rbf(X1, X2, length_scale=1.0, sigma_f=1.0):
"""
Radial Basis Function (RBF) kernel (also known as the Gaussian kernel).
Args:
X1 (array-like): First set of input points.
X2 (array-like): Second set of input points.
length_scale (float): Length scale parameter of the RBF kernel.
sigma_f (float): Signal variance parameter of the RBF kernel.
Returns:
ndarray: Covariance matrix.
"""
sqdist = cdist(X1, X2, "sqeuclidean")
return sigma_f**2 * np.exp(-0.5 / length_scale**2 * sqdist)
# Gaussian Process Regression
class GaussianProcess:
"""
Gaussian Process Regression model.
Args:
kernel (callable): Covariance function.
noise (float): Noise term for numerical stability.
"""
def __init__(self, kernel, noise=1e-10):
self.kernel = kernel
self.noise = noise
def fit(self, X, y):
"""
Fit the Gaussian Process model.
Args:
X (array-like): Training input samples.
y (array-like): Training target values.
"""
self.X_train = np.array(X)
self.y_train = np.array(y)
self.K = self.kernel(self.X_train, self.X_train) + self.noise**2 * np.eye(
len(self.X_train)
)
self.L = np.linalg.cholesky(self.K)
self.alpha = np.linalg.solve(self.L.T, np.linalg.solve(self.L, self.y_train))
def predict(self, X):
"""
Predict using the Gaussian Process model.
Args:
X (array-like): Input samples for prediction.
Returns:
tuple: Mean and variance of the predictions.
"""
K_trans = self.kernel(X, self.X_train)
K_test = self.kernel(X, X)
mu = K_trans @ self.alpha
v = np.linalg.solve(self.L, K_trans.T)
cov = K_test - v.T @ v
return mu, np.diag(cov)
# Expected Improvement
def expected_improvement(X, gp, y_max, xi=0.01):
"""
Compute the Expected Improvement acquisition function.
Args:
X (array-like): Input samples.
gp (GaussianProcess): Fitted Gaussian Process model.
y_max (float): Maximum observed value of the objective function.
xi (float): Exploration-exploitation trade-off parameter.
Returns:
ndarray: Expected Improvement values for the input samples.
"""
mu, sigma = gp.predict(X)
sigma = np.sqrt(sigma)
with np.errstate(divide="warn"):
imp = mu - y_max - xi
Z = imp / sigma
ei = imp * norm.cdf(Z) + sigma * norm.pdf(Z)
ei[sigma == 0.0] = 0.0
return ei
# Bayesian Optimization
def bayesian_optimization(obj, bounds, n_iter=10, num_init_samples=2, seed=42):
"""
Perform Bayesian Optimization on the objective function.
Args:
obj (callable): Objective function to be minimized.
bounds (array-like): Bounds of the search space.
n_iter (int): Number of optimization iterations.
num_init_samples (int): Number of initial random samples.
seed (int): Random seed for reproducibility.
Returns:
tuple: Optimal input value and list of results for each iteration.
"""
# Seed for random generator
rng = np.random.default_rng(seed)
X_sample = rng.uniform(bounds[0], bounds[1], size=(num_init_samples, 1))
y_sample = obj(X_sample).reshape(-1, 1)
# Store all results for animation
results = []
# Prior (without any data points)
gp = GaussianProcess(kernel=kernel_rbf)
results.append((gp, np.empty((0, 1)), np.empty((0, 1))))
for i in range(n_iter):
gp = GaussianProcess(kernel=kernel_rbf)
gp.fit(X_sample, y_sample)
results.append((gp, X_sample.copy(), y_sample.copy()))
EI = lambda x: -expected_improvement(x.reshape(-1, 1), gp, np.max(y_sample))
res = minimize(
EI,
rng.uniform(bounds[0], bounds[1], size=(1,)),
bounds=[bounds],
method="L-BFGS-B",
)
X_new = res.x.reshape(1, -1)
y_new = obj(X_new).reshape(-1, 1)
X_sample = np.vstack((X_sample, X_new))
y_sample = np.vstack((y_sample, y_new))
# Add GP for the final iteration
gp = GaussianProcess(kernel=kernel_rbf)
gp.fit(X_sample, y_sample)
results.append((gp, X_sample.copy(), y_sample.copy()))
# Find the x value that gives the minimum y value
idx_min = np.argmin(y_sample)
x_opt = X_sample[idx_min]
return x_opt, results
def plot_gp_animation(results, bounds, objective):
x = np.linspace(bounds[0], bounds[1], 1000).reshape(-1, 1)
frames = []
steps = []
for i, (gp, X_sample, y_sample) in enumerate(results):
if i == 0:
mu = np.zeros_like(x).flatten()
sigma = np.ones_like(x).flatten()
initial_state = (mu.copy(), sigma.copy(), X_sample.copy(), y_sample.copy())
else:
mu, sigma = gp.predict(x)
mu = mu.flatten()
sigma = sigma.flatten()
frame = go.Frame(
data=[
go.Scatter(
x=x.flatten(),
y=objective(x).flatten(),
mode="lines",
name="Objective Function",
),
go.Scatter(
x=x.flatten(),
y=mu,
mode="lines",
name="GP (Mean)",
line=dict(dash="dash"),
),
go.Scatter(
x=np.concatenate([x.flatten(), x.flatten()[::-1]]),
y=np.concatenate([mu - 1.96 * sigma, (mu + 1.96 * sigma)[::-1]]),
fill="toself",
fillcolor="rgba(255, 0, 0, 0.2)",
line=dict(color="rgba(255, 0, 0, 0)"),
hoverinfo="skip",
showlegend=False,
),
go.Scatter(
x=X_sample.flatten(),
y=y_sample.flatten(),
mode="markers",
name="Samples",
marker=dict(color="red", size=14),
),
go.Scatter(
x=[X_sample[-1][0]] if len(X_sample) > 0 else [],
y=[y_sample[-1][0]] if len(y_sample) > 0 else [],
mode="markers",
marker=dict(color="orange", size=16),
name="Latest Sample",
),
go.Scatter(
x=[X_sample[np.argmin(y_sample)][0]] if len(y_sample) > 0 else [],
y=[y_sample[np.argmin(y_sample)][0]] if len(y_sample) > 0 else [],
mode="markers+text",
marker=dict(color="green", size=18),
text=(
[
f"Optimum: x={X_sample[np.argmin(y_sample)][0]:.2f}, f(x)={y_sample[np.argmin(y_sample)][0]:.2f}"
]
if len(y_sample) > 0
else []
),
textposition="top center",
name="Current Optimum",
),
],
name=f"Iteration {i}",
)
frames.append(frame)
steps.append(
dict(
label=f"Iteration {i}",
method="animate",
args=[
[f"Iteration {i}"],
{"frame": {"duration": 1000, "redraw": True}, "mode": "immediate"},
],
)
)
fig = go.Figure(
data=frames[0].data,
layout=go.Layout(
title=dict(
text="Ilustration of Bayesian Optimization with Gaussian Proccess",
x=0.45,
y=0.90,
xanchor="center",
yanchor="top",
),
xaxis=dict(range=[bounds[0], bounds[1]], title="x"),
yaxis=dict(title="f(x)"),
width=1080,
height=720,
updatemenus=[
{
"buttons": [
{
"args": [
None,
{
"frame": {"duration": 1000, "redraw": True},
"fromcurrent": True,
},
],
"label": "Play",
"method": "animate",
},
{
"args": [
[None],
{
"frame": {"duration": 0, "redraw": True},
"mode": "immediate",
"transition": {"duration": 0},
},
],
"label": "Pause",
"method": "animate",
},
],
"direction": "right",
"showactive": False,
"type": "buttons",
"x": 1.17,
"xanchor": "right",
"y": 0.78,
"yanchor": "top",
},
{
"buttons": steps,
"direction": "down",
"showactive": True,
"x": 1.17,
"xanchor": "right",
"y": 0.70,
"yanchor": "top",
"type": "dropdown",
"bgcolor": "rgba(255, 255, 255, 0.8)",
},
],
),
frames=frames,
)
# Save as HTML file
fig.write_html(
"bayesian_optimization_animation.html", auto_open=True, auto_play=False
)
# or show it
# fig.show()
# Example of objective function
def objective(X):
return np.sin(-3 * X) + np.sin(X) + 0.2 * X**2 + 0.1 * X
# Perform Bayesian Optimization
bounds = np.array([-4, 4])
x_opt, results = bayesian_optimization(objective, bounds, n_iter=15, seed=111)
# Plot the optimization process
plot_gp_animation(results, bounds, objective)Referensi
- A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning
- Practical Bayesian Optimization of Machine Learning Algorithms
- Bayesian optimization – Borealis AI
- Gaussian Process Regression (wustl.edu)








